La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

Planear la trayectoria con jerk mínimo para el brazo robótico

Este ejemplo muestra cómo planificar una trayectoria polinómica con jerk mínimo para un manipulador robótico. El ejemplo muestra cómo cargar un modelo de robot, planificar una ruta para el modelo de robot en un entorno con obstáculos, generar una trayectoria con jerk mínimo a partir de la ruta y visualizar las trayectorias generadas y el movimiento del robot.

Configurar el entorno y el modelo de robot

Este ejemplo usa un modelo del KUKA LBR iiwa, un robot manipulador con 7 grados de libertad. Use loadrobot para cargar el modelo de robot en el área de trabajo como un objeto rigidBodyTree. Establezca el formato de salida para las configuraciones en "row".

robot = loadrobot("kukaIiwa14","DataFormat","row");

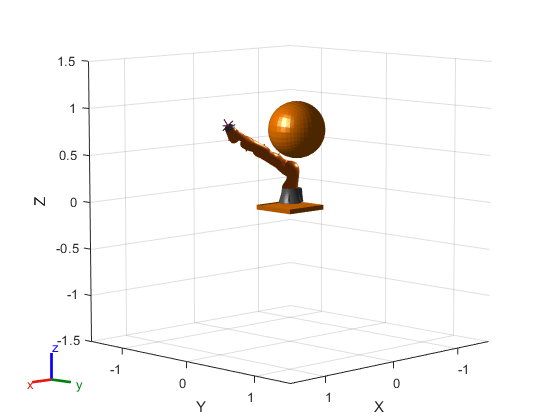
Genere el entorno para el robot. Cree objetos de colisión y especifique sus poses respecto a la base del robot. Visualice el entorno.

env = {collisionBox(0.5,0.5,0.05) collisionSphere(0.3)};
env{1}.Pose(3,end) = -0.05;
env{2}.Pose(1:3,end) = [0.1 0.2 0.8];

show(robot);
hold on
show(env{1})
show(env{2})

Planificar una ruta usando manipulatorRRT

Cree el planificador RRT para el modelo de robot usando manipulatorRRT. Configure la propiedad ValidationDistance para aumentar el número de estados intermedios al interpolar la ruta.

rrt = manipulatorRRT(robot,env);
rrt.ValidationDistance = 0.2;
rrt.SkippedSelfCollisions = "parent";

Especifique una configuración de inicio y una de objetivo.

startConfig = [0.08 -0.65 0.05 0.02 0.04 0.49 0.04];
goalConfig =  [2.97 -1.05 0.05 0.02 0.04 0.49 0.04];

Planifique la ruta. Debido a la aleatoriedad del algoritmo RRT, establezca el valor inicial rng para la repetibilidad.

rng(0)
path = plan(rrt,startConfig,goalConfig);

Interpole la ruta y recupere los waypoints.

interpPath = interpolate(rrt,path);
wpts = interpPath';

Generar una trayectoria polinómica con jerk mínimo

El planificador devuelve una ruta como un conjunto ordenado de waypoints. Para pasarlos a un robot, primero debe determinar una trayectoria a través de ellos. La función minjerkpolytraj crea una trayectoria sin obstáculos con jerk mínimo que llega a todos los waypoints especificados.

Especifique una estimación inicial de los puntos de tiempo en que el brazo robótico llega a los waypoints.

initialGuess = linspace(0,size(wpts,2)*0.2,size(wpts,2));

Especifique el número de muestras a tomar al estimar la trayectoria.

numSamples = 100;

Calcule la trayectoria polinómica con jerk mínimo.

[q,qd,qdd,qddd,pp,tpts,tSamples] = minjerkpolytraj(wpts,initialGuess,numSamples);

Visualizar trayectorias y waypoints

Represente las trayectorias y los waypoints a lo largo del tiempo.

minJerkPath = q';
figure
plot(tSamples,q)
hold all
plot(tpts,wpts,"x")

Visualizar el movimiento del robot

Use la función de objeto show para animar el movimiento resultante. Esta visualización permite actualizaciones rápidas para garantizar una animación fluida.

figure;
ax = show(robot,startConfig);
hold all

% Ensure the figure pops out of the Live Editor so animations are visible
set(gcf,"Visible","on");
for i = 1:length(env)
    show(env{i},"Parent",ax);
end

for i = 1:size(minJerkPath,1)
    show(robot,minJerkPath(i,:),"PreservePlot",false,"FastUpdate",true);
    drawnow;
end

hold off