labelSpectrogramOptions

Spectrogram options for time-frequency label definition

Since R2025a

Description

Use a labelSpectrogramOptions object to store spectrogram options for signal labeling in the time-frequency domain. You can use spectrogram options to create time-frequency region-of-interest (ROI) label definitions.

Creation

Syntax

opts = labelSpectrogramOptions

opts = labelSpectrogramOptions(resType)

opts = labelSpectrogramOptions(resType,PropertyName=Value)

Description

opts = labelSpectrogramOptions creates an object, opts, that stores the spectrogram options with default values.

opts = labelSpectrogramOptions(resType) also specifies how to divide a signal into segments when constructing its spectrogram.

opts = labelSpectrogramOptions(resType,PropertyName=Value) specifies additional properties using name-value arguments. You can specify multiple name-value arguments. For example, the spectrograms in this object use Kaiser windows with automatically chosen length, 50 dB sidelobe attenuation, and 90% overlap between adjoining segments.

opts = labelSpectrogramOptions("rbw",Overlap=90, ...
    Window="kaiser",WindowAttenuationKaiser=50)

Input Arguments

resType — Spectrogram resolution type

"leakage" (default) | "rbw" | "windowlength"

Spectrogram resolution type, specified as "leakage", "rbw", or "windowlength". This argument sets the ResolutionType property.

There are three ways in which you can divide a signal into segments:

• Divide Signal into Segments: Control Leakage

• Divide Signal into Segments: Control Resolution Bandwidth

• Divide Signal into Segments: Control Window Length

This table lists the properties that you can specify as name-value arguments depending on how you choose to divide the signal.

Leakage	Resolution Bandwidth (RBW)	Window Length
Leakage TimeResolutionMode TimeResolution Reassign	RBWMode RBW Window WindowAttenuationChebyshev WindowAttenuationKaiser	WindowLengthMode WindowLength Window WindowAttenuationChebyshev WindowAttenuationKaiser NFFTMode NFFT

In addition, you can specify these properties for any resolution type: Overlap, MinimumThresholdMode, MinimumThreshold, and UseDecibels.

Properties

All resolution types

ResolutionType — Spectrogram resolution type

"leakage" (default) | "rbw" | "windowlength"

Spectrogram resolution type, returned as "leakage", "rbw", or "windowlength".

To set this property, use resType. After you create an object, you can modify this property using dot notation. For more information about dot notation, see Access Property Values.

Data Types: char | string

Overlap — Percentage of overlapped samples between adjoining segments

50 (default) | nonnegative scalar less than 100

Percentage of overlapped samples between adjoining segments, specified as a nonnegative scalar less than 100. To learn more about how labelSpectrogramOptions interprets Overlap depending on how you choose to divide a signal into segments, see Spectrogram Options for Time-Frequency Labeling.

Data Types: single | double

MinimumThresholdMode — Mode to set spectrogram minimum threshold

"auto" (default) | "specify"

Mode to set the minimum threshold in the spectrogram computation, specified as one of these:

• "auto" — labelSpectrogramOptions automatically sets the minimum threshold of the spectrogram.

• "specify" — You can use MinimumThreshold to specify the minimum threshold of the spectrogram.

Data Types: char | string

MinimumThreshold — Minimum threshold for spectrogram

[] (default) | positive scalar

Minimum threshold for the spectrogram, specified as a real-valued scalar expressed in decibels. MinimumThreshold represents the lower bound for nonzero values in the spectrogram computation.

To specify this property, set MinimumThresholdMode to "specify".

Data Types: single | double

UseDecibels — Option to express spectrogram magnitude in decibels

1 or true (default) | 0 or false

Option to express spectrogram magnitude in decibels, specified as 1 (true) or 0 (false).

Data Types: single | double | logical

Specific to Resolution Type

Leakage — Spectral leakage

20 (default) | nonnegative scalar less than or equal to 40

Spectral leakage, specified as a nonnegative scalar less than or equal to 40.

Leakage controls the window sidelobe attenuation relative to the mainlobe width, balancing between improving resolution and decreasing leakage:

• A large leakage value resolves closely spaced tones but masks nearby weak tones.

• A small leakage value finds small tones in the vicinity of larger tones but smears close frequencies together.

For more information, see Leakage.

To specify this property, set resType to "leakage".

Data Types: single | double

TimeResolutionMode — Mode to set time resolution

"auto" (default) | "specify"

Mode to set the time resolution in the spectrogram computation, specified as one of these:

• "auto" — labelSpectrogramOptions automatically sets the time resolution of the spectrogram.

• "specify" — You can use TimeResolution to specify the time resolution of the spectrogram.

For more information, see Time Resolution.

To specify this property, set resType to "leakage".

Data Types: char | string

TimeResolution — Time resolution of spectrogram

[] (default) | positive scalar

Time resolution of the spectrogram, specified as a positive scalar. For more information, see Time Resolution.

To specify this property, set TimeResolutionMode to "specify".

Data Types: single | double

Reassign — Option to reassign spectrogram values

0 or false (default) | 1 or true

Option to reassign spectrogram values, specified as 0 (false) or 1 (true).

If you set Reassign to true, then labelSpectrogramOptions sets the spectrogram computation to sharpen the localization of spectral estimates by performing time and frequency reassignment. The reassignment technique produces periodograms and spectrograms that are easier to read and interpret. This technique reassigns each spectral estimate to the center of energy of its bin instead of the bin's geometric center. The technique provides exact localization for chirps and impulses.

To specify this property, set resType to "leakage".

Data Types: single | double | logical

RBWMode — Mode to set resolution bandwidth

"auto" (default) | "specify"

Mode to set the resolution bandwidth in the spectrogram computation, specified as one of these:

• "auto" — labelSpectrogramOptions automatically sets the resolution bandwidth of the spectrogram.

• "specify" — You can use RBW to specify the resolution bandwidth of the spectrogram.

For more information, see RBW and Segment Length.

To specify this property, set resType to "rbw".

Data Types: char | string

RBW — Resolution bandwidth

[] (default) | positive scalar

Resolution bandwidth of the spectrogram, specified as a positive scalar.

For more information, see RBW and Segment Length.

To specify this property, set RBWMode to "specify".

Data Types: single | double

Window — Type of window

"hamming" (default) | "blackmanharris" | "flattop" | "hann" | "rectangular" | "chebyshev" | "kaiser"

Type of window, specified as "hamming", "blackmanharris", "flattop", "hann", "rectangular", "chebyshev", or "kaiser". For more information, see Windows.

To specify this property, set resType to "rbw" or "windowlength".

Data Types: single | double | logical

WindowAttenuationChebyshev — Sidelobe attenuation of Chebyshev window

[] (default) | scalar greater than or equal to 21

Sidelobe attenuation of Chebyshev window, specified in decibels as a scalar greater than or equal to 21.

To specify this property, set Window to "chebyshev".

Data Types: single | double

WindowAttenuationKaiser — Sidelobe attenuation of Kaiser window

[] (default) | scalar greater than or equal to 45

Sidelobe attenuation of Kaiser window, specified in decibels as a scalar greater than or equal to 45.

To specify this property, set Window to "kaiser".

Data Types: single | double

WindowLengthMode — Mode to set window length

"auto" (default) | "specify"

Mode to set window length in the spectrogram computation, specified as one of these:

• "auto" — labelSpectrogramOptions automatically sets the window length of the spectrogram.

• "specify" — You can use WindowLength to specify the window length of the spectrogram.

For more information, see Window Length and Segment Length.

To specify this property, set resType to "windowlength".

Data Types: char | string

WindowLength — Window length

[] (default) | positive integer

Window length, specified as a positive integer.

For more information, see Window Length and Segment Length.

To specify this property, set WindowLengthMode to "specify".

Data Types: single | double

NFFTMode — Mode to set number of DFT points

"auto" (default) | "specify"

Mode to set number of discrete Fourier transform (DFT) points in the spectrogram computation, specified as one of these:

• "auto" — labelSpectrogramOptions automatically sets the number of DFT points used to calculate the spectrogram.

• "specify" — You can use NFFT to specify the number of DFT points used to calculate the spectrogram.

For more information, see Number of DFT Points.

To specify this property, you must:

• Set resType to "windowlength".

• Set WindowLengthMode to "specify".

• Specify a value in WindowLength.

Data Types: char | string

NFFT — Number of DFT points

[] (default) | positive integer

Number of discrete Fourier transform (DFT) points used to calculate the spectrogram, specified as a positive integer. The number of DFT points must be greater than or equal to the window length.

For more information, see Number of DFT Points.

To specify this property, set NFFTMode to "specify".

Data Types: single | double

Object Functions

Examples

Define Time-Frequency Label with Spectrogram Options

Create a set of spectrogram options for a signal label definition. Specify a Hamming window with a length of 1024 samples.

 opts = labelSpectrogramOptions("windowlength", ...
     Overlap=50, ...
     Window="hamming", ...
     WindowLengthMode="specify",WindowLength=1024)

opts = 
  labelSpectrogramOptions with properties:

          ResolutionType: "windowlength"
                 Overlap: 50
                  Window: "hamming"
        WindowLengthMode: "specify"
            WindowLength: 1024
                NFFTMode: "auto"
    MinimumThresholdMode: "auto"
             UseDecibels: 1

Create a time-frequency ROI signal label definition with time-frequency options.

 signalLabelDefinition("LowBand", ...
     LabelType="roiTimeFrequency",TimeFrequencyOptions=opts);

Label Signal in Time-Frequency Domain

Label Gaussian atoms in the time-frequency domain using a time-frequency region-of-interest (ROI) label definition and spectrogram options.

Generate Signal and Visualize Spectrogram

Generate a signal that consists of a voltage-controlled oscillator and four Gaussian atoms. The signal is sampled at 14 kHz for two seconds. Plot the spectrogram of the signal.

Fs = 14000;
t = (0:1/Fs:2)';
st = 0.01;
gaussFun = @(A,x,mu,f) exp(-(x-mu).^2/(2*st^2)).*sin(2*pi*f.*x)*A';
atomTimeCenters = [0.2 0.5 1 1.75];
atomFreqCenters = [2 6 2 5]*1000;
s = gaussFun([1 1 1 1]/10,t,atomTimeCenters,atomFreqCenters);
x = vco(chirp(t+.1,0,t(end),3).*exp(-2*(t-1).^2),[0.1 0.4]*Fs,Fs);
s = s/10+x;

bt = 0.2;
tr = 0.05;
op = 99;
pspectrum(s,Fs,"spectrogram", ...
    Leakage=bt,TimeResolution=tr,OverlapPercent=op)

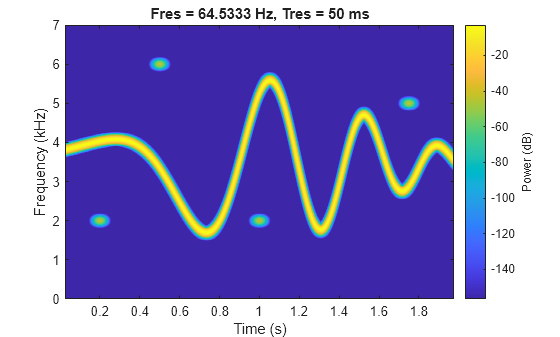
The spectrogram shows four patches in time-frequency domain that correspond with the Gaussian atoms. Define the times and frequencies for all the atoms.

atomTimes = atomTimeCenters'+[-st st]*5.5;
atomFreqs = atomFreqCenters'+[-1 1]*200;

Label Signal in Time-Frequency Domain

Create a logical time-frequency ROI label definition to label the Gaussian atoms. Specify spectrogram options with leakage properties.

opts = labelSpectrogramOptions("leakage", ...
    Leakage=40*(1-bt),Overlap=op, ...
    TimeResolutionMode="specify",TimeResolution=tr);

lblDef = signalLabelDefinition("Atom", ...
    LabelDataType="logical", ...
    LabelType="roiTimeFrequency",TimeFrequencyOptions=opts);

Create a labeled signal set from the signal and time-frequency ROI label definition.

lss = labeledSignalSet(s,lblDef,SampleRate=Fs);

Label the four atoms in time-frequency domain. Set the label values to true.

setLabelValue(lss,1,"Atom",atomTimes,atomFreqs,true(1,4))

Visualize Time-Frequency Image and Label Mask

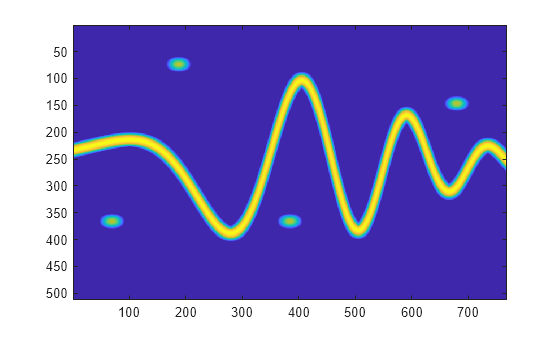
Create datastores from the labeled signal set for the time-frequency ROI label.

imSize = [512 768];
[sds,ads] = createDatastores(lss,"Atom", ...
    TimeFrequencyMapFormat="image", ...
    TimeFrequencyImageSize=imSize, ...
    TimeFrequencyLabelFormat="mask", ...
    TimeFrequencyMaskPriority=true);

Read and show the time-frequency image.

imagesc(read(sds))

Read the label mask and display it above the time-frequency image.

lbl = read(ads);
im = zeros([imSize 3]);
im(:,:,1) = lbl{1};
hold on
imagesc(im,AlphaData=0.5*lbl{1})
hold off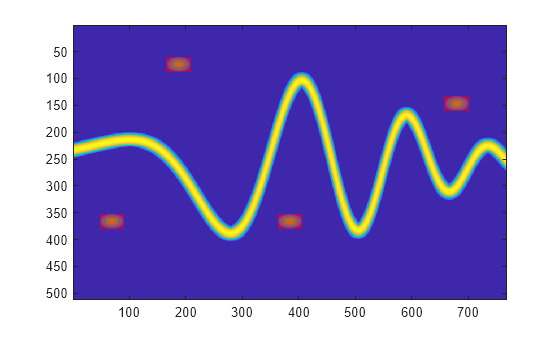

More About

Spectrogram Options for Time-Frequency Labeling

A nonstationary signal is a signal whose frequency content changes with time. The spectrogram of a nonstationary signal is an estimate of the time evolution of its frequency content. To construct the spectrogram of a nonstationary signal, labelSpectrogramOptions follows these steps:

1. Divide the signal into equal-length windowed segments that may or may not overlap. For best results, choose a segment length short enough that the frequency content of the signal does not change appreciably within a segment. There are three ways of dividing a signal into segments:

   • Divide Signal into Segments: Control Leakage

   • Divide Signal into Segments: Control Resolution Bandwidth

   • Divide Signal into Segments: Control Window Length

2. Compute the spectrum of each segment over a set of discrete Fourier transform points to get the short-time Fourier transform.

3. Display segment by segment the magnitude squared of each spectrum in decibels. Depict the magnitudes side by side as an image with magnitude-dependent colormap.

Divide Signal into Segments: Control Leakage

If you set resType to "leakage":

• You can specify the leakage, time resolution, and the overlap between adjoining segments.

• You can also specify a MinimumThreshold and the option to UseDecibels in the spectrogram magnitude.

• labelSpectrogramOptions uses 1024 DFT points.

Leakage

If you divide the signal into segments by controlling the leakage, labelSpectrogramOptions uses Kaiser windows, which have an adjustable shape factor β that is related to the leakage ℓ by β = 40(1 – ℓ). When you specify Leakage, labelSpectrogramOptions assumes that the specified value corresponds to β.

Choosing a β value is equivalent to specifying the sidelobe attenuation of the Kaiser window. If α is the attenuation in dB, the two quantities are related by

$$\beta =\{\begin{array}{ll}0.1102(\alpha -8.7),\hfill & \alpha >50\hfill \\ 0.5842{(\alpha -21)}^{0.4}+0.07886(\alpha -21),\hfill & 50\ge \alpha \ge 21\hfill \\ 0,\hfill & \alpha <21\hfill \end{array}$$

• The minimum value in the Leakage range corresponds to a Kaiser window with β = 0, equivalent to a rectangular window with a narrow mainlobe and large sidelobes.

• An intermediate value of β ≈ 6 approximates a Hann window closely.

• The maximum value in the Leakage range corresponds to a Kaiser window with β = 40, where a wide mainlobe captures essentially all the spectral energy representable in double precision and the energy contained in the sidelobes becomes negligible.

Time Resolution

• By default, labelSpectrogramOptions uses the length of the entire signal to choose the segment length. The object sets the time resolution as ⌈N/d⌉ samples, where the brackets denote the ceiling function, N is the length of the signal, and d is a divisor that depends on N.

  Signal Length (N)	Divisor (d)	Segment Length
  2 samples – 63 samples	2	1 sample – 32 samples
  64 samples – 255 samples	8	8 samples – 32 samples
  256 samples – 2047 samples	8	32 samples – 256 samples
  2048 samples – 4095 samples	16	128 samples – 256 samples
  4096 samples – 8191 samples	32	128 samples – 256 samples
  8192 samples – 16383 samples	64	128 samples – 256 samples
  16384 samples – N samples	128	128 samples – ⌈N / 128⌉ samples

• To set the time resolution, set TimeResolutionMode to "specify" and specify a value in TimeResolution in one of these formats:

  • If the signal does not have time information, specify the time resolution (segment length) in samples. The time resolution must be an integer greater than or equal to 1 and smaller than or equal to the signal length.

  • If the signal has time information, specify the segment length in seconds. The object converts the result into a number of samples and rounds it to the nearest integer that is less than or equal to the number but not smaller than 1. The time resolution must be smaller than or equal to the signal duration.

Overlap

Specify the overlap as a percentage of the segment length in the Overlap property. The default value is 50%. The object converts the value into a number of samples and rounds it to the nearest integer that is less than or equal to the number.

Specifying the overlap changes the number of segments. The larger the overlap, the larger the number of segments. The object zero-pads segments that extend beyond the signal endpoint. For example, consider the seven-sample signal [s0 s1 s2 s3 s4 s5 s6] and a window length of 4 samples.

Number of Overlapping Samples	Resulting Segments
0 (0%)	s0 s1 s2 s3 s4 s5 s6 0
1 (25%)	s0 s1 s2 s3 s3 s4 s5 s6
2 (50%)	s0 s1 s2 s3 s2 s3 s4 s5 s4 s5 s6 0
3 (75%)	s0 s1 s2 s3 s1 s2 s3 s4 s2 s3 s4 s5 s3 s4 s5 s6

Divide Signal into Segments: Control Resolution Bandwidth

If you set resType to "rbw":

• You can specify the window type, the sidelobe attenuation for some windows, the RBW, and the overlap between adjoining segments.

• You can also specify a MinimumThreshold and the option to UseDecibels in the spectrogram magnitude.

• labelSpectrogramOptions calculates the segment length and assumes the window length and the number of DFT points equal to the segment length.

Window Type and Sidelobe Attenuation

If you divide the signal into segments by controlling the resolution bandwidth, you can choose one of these spectral windows:

• Blackman-Harris

• Chebyshev

• Flat-top

• Hamming (default)

• Hann

• Kaiser

• Rectangular

You can control the sidelobe attenuation for the Chebyshev and Kaiser windows. Specify the desired attenuation in WindowAttenuationChebyshev or in WindowAttenuationKaiser, as a positive number in decibels.

• For a Chebyshev window, all sidelobes have an amplitude smaller than the mainlobe level by the specified attenuation value. The specified value must be at least 45 dB.

• For a Kaiser window, the highest sidelobe has an amplitude smaller than the mainlobe level by the specified attenuation value. The specified value must be at least 21 dB. Choosing a sidelobe attenuation of α dB is equivalent to specifying this β value:

  $$\beta =\{\begin{array}{ll}0.1102(\alpha -8.7),\hfill & \alpha >50\hfill \\ 0.5842{(\alpha -21)}^{0.4}+0.07886(\alpha -21),\hfill & 50\ge \alpha \ge 21\hfill \\ 0,\hfill & \alpha <21\hfill \end{array}$$

RBW and Segment Length

If you divide the signal into segments by controlling the resolution bandwidth (RBW), labelSpectrogramOptions uses RBW, if specified, to determine the segment length for spectrogram computation.

• To specify the RBW, set RBWMode to "specify" and specify a value in RBW. labelSpectrogramOptions determines the segment length iteratively by solving this equation:

  $$\text{Window length}=\lceil \frac{\text{Sample rate}}{\text{RBW}}\times \frac{{\displaystyle \sum _{n=1}^{\text{Window length}}{\left|\text{Window}\left(n\right)\right|}^2}}{{\left|{\displaystyle \sum _{n=1}^{\text{Window length}}\text{Window}\left(n\right)}\right|}^2}\rceil .$$

• If you do not specify RBW or if you set RBWMode to "auto", labelSpectrogramOptions chooses a segment length of ⌈N/d⌉ samples, where the brackets denote the ceiling function, N is the signal length, and d is a divisor that depends on N.

  Signal Length (N)	Divisor (d)	Segment Length
  2 samples – 63 samples	2	1 sample – 32 samples
  64 samples – 255 samples	8	8 samples – 32 samples
  256 samples – 2047 samples	8	32 samples – 256 samples
  2048 samples – 4095 samples	16	128 samples – 256 samples
  4096 samples – 8191 samples	32	128 samples – 256 samples
  8192 samples – 16383 samples	64	128 samples – 256 samples
  16384 samples – N samples	128	128 samples – ⌈N / 128⌉ samples

Overlap

Specify the overlap as a percentage of the segment length in the Overlap property. The default value is 50%. The object converts the value into a number of samples and rounds it to the nearest integer that is less than or equal to the number.

Specifying the overlap changes the number of segments. The larger the overlap, the larger the number of segments. The object drops segments that extend beyond the signal endpoint. For example, consider the seven-sample signal [s0 s1 s2 s3 s4 s5 s6] and a window length of 4 samples.

Number of Overlapping Samples	Resulting Segments
0 (0%)	s0 s1 s2 s3
1	s0 s1 s2 s3 s3 s4 s5 s6
2	s0 s1 s2 s3 s2 s3 s4 s5
3	s0 s1 s2 s3 s1 s2 s3 s4 s2 s3 s4 s5 s3 s4 s5 s6

Note

You cannot specify 100% overlap. The maximum attainable value corresponds to one sample less than the window length. If you specify that value, labelSpectrogramOptions divides the signal into [Signal length – (Window length – 1)] segments.

Divide Signal into Segments: Control Window Length

If you set resType to "windowlength":

• You can specify the window length, window type, the sidelobe attenuation for some windows, the number of DFT points, and the overlap between adjoining segments.

• You can also specify a MinimumThreshold and the option to UseDecibels in the spectrogram magnitude.

• labelSpectrogramOptions calculates the window length if unspecified, and assumes the segment length equal to the window length.

Window Length and Segment Length

If you divide the signal into segments by controlling the window length, labelSpectrogramOptions uses the window length, if specified, to determine the segment length for spectrogram computation. The segment length equals to the window length.

• To specify the window length, set WindowLengthMode to "specify" and specify a value in WindowLength. in samples.

• If you do not specify WindowLength or if you set WindowLengthMode to "auto", labelSpectrogramOptions uses a window length

  $$\text{Window length}=\lfloor \frac{\text{Signal length}}{8-7\times \frac{\text{Overlap percent}}{100}}\rfloor$$

  so that the signal is divided into eight segments with ⌊Window length × Overlap percent/100⌋ samples of overlap between adjoining segments. The ⌊⌋ symbols denote the floor function.

Window Type and Sidelobe Attenuation

If you divide the signal into segments by controlling the resolution bandwidth, you can choose one of these spectral windows:

• Blackman-Harris

• Chebyshev

• Flat-top

• Hamming (default)

• Hann

• Kaiser

• Rectangular

You can control the sidelobe attenuation for the Chebyshev and Kaiser windows. Specify the desired attenuation in WindowAttenuationChebyshev or in WindowAttenuationKaiser, as a positive number in decibels.

• For a Chebyshev window, all sidelobes have an amplitude smaller than the mainlobe level by the specified attenuation value. The specified value must be at least 45 dB.

• For a Kaiser window, the highest sidelobe has an amplitude smaller than the mainlobe level by the specified attenuation value. The specified value must be at least 21 dB. Choosing a sidelobe attenuation of α dB is equivalent to specifying this β value:

  $$\beta =\{\begin{array}{ll}0.1102(\alpha -8.7),\hfill & \alpha >50\hfill \\ 0.5842{(\alpha -21)}^{0.4}+0.07886(\alpha -21),\hfill & 50\ge \alpha \ge 21\hfill \\ 0,\hfill & \alpha <21\hfill \end{array}$$

Overlap

You can specify the window length and the overlap between adjoining segments simultaneously. Specify the overlap as a percentage of the segment length in the Overlap property. The default value is 50%. The object converts the value into a number of samples and rounds it to the nearest integer that is less than or equal to the number.

Specifying the overlap changes the number of segments. The larger the overlap, the larger the number of segments. The object drops segments that extend beyond the signal endpoint.

For example, consider the seven-sample signal [s0 s1 s2 s3 s4 s5 s6] and a window length of 4 samples.

Number of Overlapping Samples	Resulting Segments
0 (0%)	s0 s1 s2 s3
1 (25%)	s0 s1 s2 s3 s3 s4 s5 s6
2 (50%)	s0 s1 s2 s3 s2 s3 s4 s5
3 (75%)	s0 s1 s2 s3 s1 s2 s3 s4 s2 s3 s4 s5 s3 s4 s5 s6

Note

You cannot specify 100% overlap. The maximum attainable value corresponds to one sample less than the window length. If you specify that value, labelSpectrogramOptions divides the signal into [Signal length – (Window length – 1)] segments.

Number of DFT Points

If you adjust the spectral resolution by controlling the window length, you can specify the number of DFT points, NFFT.

• By default, labelSpectrogramOptions uses the window length to set NFFT.

• To set NFFT, set NFFTMode to "specify" and specify a value in NFFT. NFFT must be greater than or equal to the window length.

Version History

Introduced in R2025a