Espectro cruzado y coherencia de magnitud cuadrada
Este ejemplo muestra cómo utilizar el espectro cruzado para obtener el desfase entre componentes sinusoidales en una serie de tiempo bivariada. El ejemplo también utiliza la coherencia de magnitud cuadrada para identificar una correlación de dominio de frecuencia significativa en las frecuencias de onda sinusoidal.
Cree la serie de tiempo bivariada. La serie individual consta de dos ondas sinusoidales con frecuencias de 100 y 200 Hz. Las series están integradas en ruido blanco gaussiano aditivo y muestreadas a 1 kHz. Ambas ondas sinusoidales de la serie x tienen amplitudes iguales a 1. La onda sinusoidal de 100 Hz de la serie y tiene una amplitud de 0,5 y la onda sinusoidal de 200 Hz de la serie y tiene una amplitud de 0,35. Las ondas sinusoidales de 100 y 200 Hz de la serie y tienen un desfase de radianes y de radianes, respectivamente. Considere la serie y como la salida corrompida por ruido de un sistema lineal con entrada x. Establezca la configuración predeterminada del generador de números aleatorios para obtener resultados reproducibles.
rng default Fs = 1000; t = 0:1/Fs:1-1/Fs; x = cos(2*pi*100*t) + sin(2*pi*200*t) + 0.5*randn(size(t)); y = 0.5*cos(2*pi*100*t - pi/4) + ... 0.35*sin(2*pi*200*t - pi/2) + 0.5*randn(size(t));
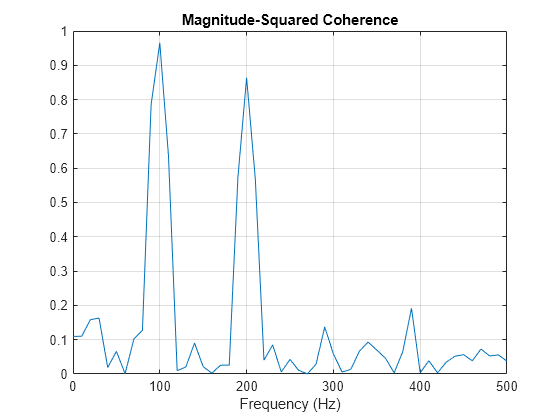
Obtenga la estimación de coherencia de magnitud cuadrada para la serie de tiempo bivariada. La coherencia de magnitud cuadrada permite identificar una correlación de dominio de frecuencia significativa entre dos series de tiempo. Las estimaciones de fase en el espectro cruzado solo son útiles si existe una correlación de dominio de frecuencia significativa.
Para evitar obtener una estimación de coherencia de magnitud cuadrada que sea 1 para todas las frecuencias, debe utilizar un estimador de coherencia promediado. Son adecuados tanto el promediado de segmentos superpuestos de Welch (WOSA) como las técnicas multitaper. mscohere implementa un estimador de WOSA.
Establezca la longitud de la ventana en 100 muestras. Esta longitud de ventana contiene 10 periodos de la onda sinusoidal de 100 Hz y 20 periodos de la onda sinusoidal de 200 Hz. Utilice un solapamiento de 80 muestras con la ventana Hamming predeterminada. Introduzca la tasa de muestreo de forma explícita para obtener las frecuencias de salida en Hz. Represente la coherencia de magnitud cuadrada. La coherencia de magnitud cuadrada es mayor que 0,8 a 100 y 200 Hz.
[Cxy,F] = mscohere(x,y,hamming(100),80,100,Fs); plot(F,Cxy) title("Magnitude-Squared Coherence") xlabel("Frequency (Hz)") grid
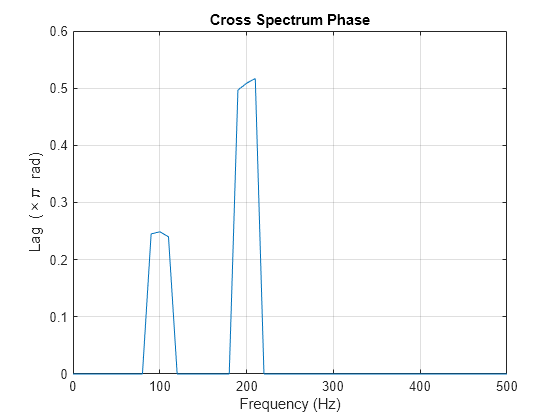
Obtenga el espectro cruzado de x e y utilizando cpsd. Utilice los mismos parámetros para obtener el espectro cruzado que utilizó en la estimación de coherencia. Ignore el espectro cruzado cuando la coherencia sea pequeña. Represente la fase del espectro cruzado e indique las frecuencias con coherencia significativa entre los dos tiempos. Marque los desfases conocidos entre los componentes sinusoidales. A 100 y 200 Hz, los desfases calculados a partir del espectro cruzado se acercan a los valores reales.
[Pxy,F] = cpsd(x,y,hamming(100),80,100,Fs); Pxy(Cxy < 0.2) = 0; plot(F,angle(Pxy)/pi) title("Cross Spectrum Phase") xlabel("Frequency (Hz)") ylabel("Lag (\times\pi rad)") grid