Filtrar datos con Signal Processing Toolbox
Filtro FIR paso bajo: método de ventana
Este ejemplo muestra cómo diseñar e implementar un filtro FIR utilizando dos funciones de la línea de comandos, fir1 y designfilt, y la app interactiva Filter Designer.
Cree una señal para utilizarla en los ejemplos. La señal es una onda sinusoidal de 100 Hz en ruido blanco gaussiano aditivo . Establezca el estado predeterminado del generador de números aleatorios para obtener resultados reproducibles.
rng("default")
Fs = 1000;
t = linspace(0,1,Fs);
x = cos(2*pi*100*t) + 0.5*randn(size(t));El diseño del filtro es un filtro FIR paso bajo con un orden igual a 20 y una frecuencia de corte de 150 Hz. Utilice una ventana de Kaiser con una longitud de una muestra mayor que el orden del filtro y . Consulte kaiser para obtener más información acerca de la ventana de Kaiser.
Utilice fir1 para diseñar el filtro. fir1 requiere frecuencias normalizadas en el intervalo [0,1], donde 1 corresponde a rad/muestra. Para utilizar fir1, debe convertir todas las especificaciones de frecuencia en frecuencias normalizadas.
Diseñe el filtro y visualice la respuesta de magnitud.
fc = 150; Wn = (2/Fs)*fc; b = fir1(20,Wn,"low",kaiser(21,3)); [h,f] = freqz(b,1,[],Fs); plot(f,mag2db(abs(h))) xlabel("Frequency (Hz)") ylabel("Magnitude (dB)") grid
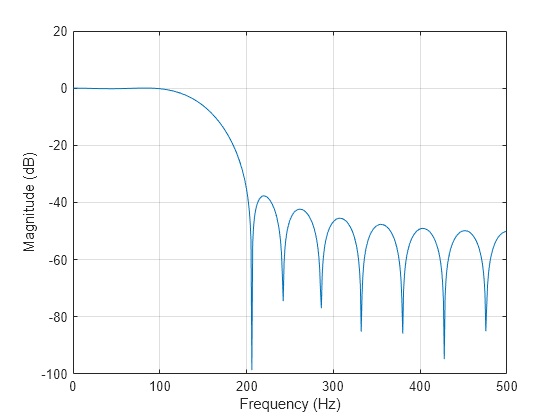
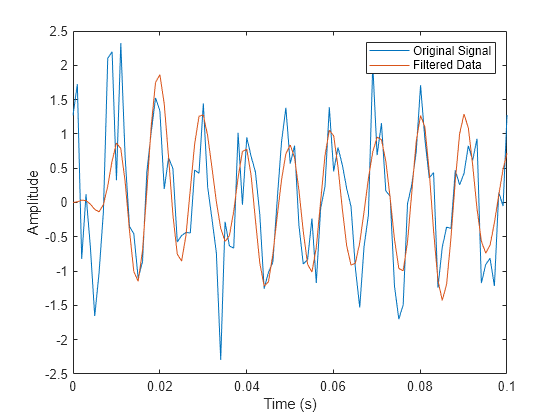
Aplique el filtro a la señal y represente el resultado para los diez primeros periodos de la sinusoide de 100 Hz.
y = filter(b,1,x); plot(t,x,t,y) xlim([0 0.1]) xlabel("Time (s)") ylabel("Amplitude") legend("Original Signal","Filtered Data")
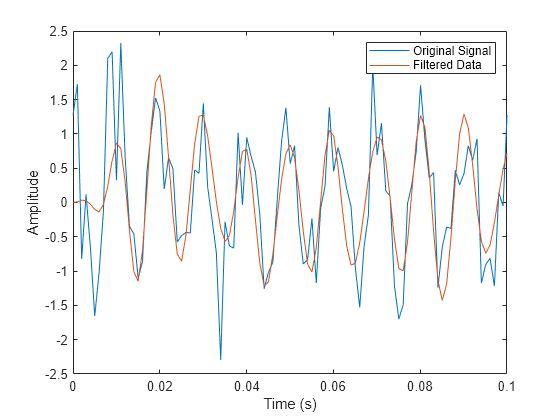
Diseñe el mismo filtro mediante designfilt. Establezca la respuesta de filtro en "lowpassfir"" e introduzca las especificaciones como pares Name,Value. Con designfilt puede especificar el diseño de filtro en Hz.
Fs = 1000; Hd = designfilt("lowpassfir",FilterOrder=20,CutoffFrequency=150, ... DesignMethod="window",Window={@kaiser,3},SampleRate=Fs);
Filtre los datos y represente el resultado.
y1 = filter(Hd,x); plot(t,x,t,y1) xlim([0 0.1]) xlabel("Time (s)") ylabel("Amplitude") legend("Original Signal","Filtered Data")
Filtro FIR paso bajo con Filter Designer
Este ejemplo muestra cómo diseñar e implementar un filtro FIR paso bajo utilizando el método de ventana con la app interactiva Filter Designer.
Inicie la app introduciendo
filterDesigneren la línea de comandos.Establezca Response Type en Lowpass.
Establezca Design Method en FIR y seleccione el método Window.
En Filter Order, seleccione Specify order. Establezca el orden en 20.
En Frequency Specifications, establezca Units en Hz, Fs en 1000 y Fc en 150.

Haga clic en Design Filter.
Seleccione File > Export... para exportar el filtro FIR al área de trabajo de MATLAB® como coeficientes o como objeto de filtro. En este ejemplo, exporte el filtro como un objeto. Especifique el nombre de variable como
Hd.

Haga clic en Export.
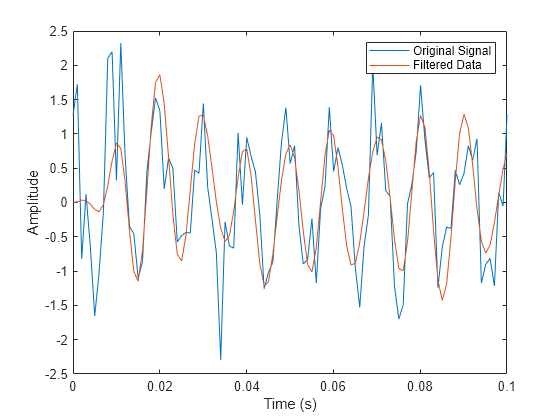
Filtre la señal de entrada de la ventana de comandos con el objeto de filtro exportado. Represente el resultado para los diez primeros periodos de la sinusoide de 100 Hz.
y2 = filter(Hd,x); plot(t,x,t,y2) xlim([0 0.1]) xlabel("Time (s)") ylabel("Amplitude") legend("Original Signal","Filtered Data")
Seleccione File > Generate MATLAB Code > Filter Design Function para generar una función de MATLAB y crear un objeto de filtro utilizando sus especificaciones.
También puede utilizar la herramienta interactiva filterBuilder para diseñar el filtro.
Filtros paso banda: sistemas FIR e IIR de orden mínimo
Este ejemplo muestra cómo diseñar un filtro paso banda y cómo filtrar datos con filtros FIR equiripple e IIR Butterworth de orden mínimo. Puede modelar muchas señales del mundo real como una superposición de componentes oscilantes, una tendencia de baja frecuencia y ruido aditivo. Por ejemplo, los datos económicos a menudo contienen oscilaciones que representan ciclos superpuestos en una tendencia ascendente o descendente que varía lentamente. Además, hay un componente de ruido aditivo que es una combinación de error de medición y de las fluctuaciones aleatorias inherentes al proceso.
En estos ejemplos, suponga que muestrea algún proceso todos los días durante un año. Suponga que el proceso tiene oscilaciones en escalas de aproximadamente una semana y un mes. Además, hay una tendencia ascendente de baja frecuencia en los datos y en el ruido blanco gaussiano aditivo .
Cree la señal como una superposición de dos ondas sinusoidales con frecuencias de 1/7 y 1/30 ciclos/día. Añada un término de tendencia en aumento de baja frecuencia y ruido blanco gaussiano . Reinicie el generador de números aleatorios para obtener resultados reproducibles. Los datos se muestrean a 1 muestra/día. Represente la señal resultante y la estimación de la densidad espectral de potencia (PSD).
rng("default") Fs = 1; n = 1:365; x = cos(2*pi*(1/7)*n) + cos(2*pi*(1/30)*n-pi/4); trend = 3*sin(2*pi*(1/1480)*n); y = x + trend + 0.5*randn(size(n)); [pxx,f] = periodogram(y,[],[],Fs); subplot(2,1,1) plot(n,y) xlim([1 365]) xlabel("Days") grid on subplot(2,1,2) plot(f,10*log10(pxx)) xlabel("Cycles/day") ylabel("dB") grid on
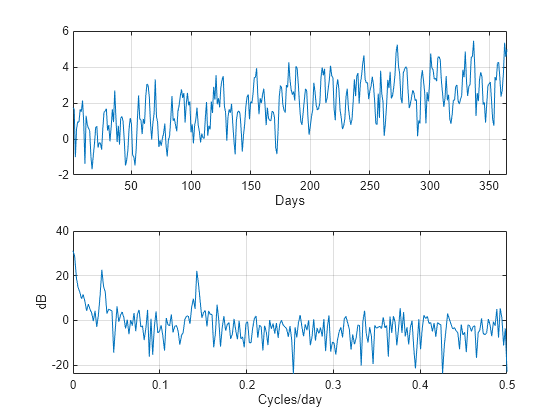
La tendencia de baja frecuencia aparece en la estimación de densidad espectral de potencia como potencia de baja frecuencia aumentada. La potencia de baja frecuencia aparece aproximadamente 10 dB por encima de la oscilación a 1/30 ciclos/día. Utilice esta información en las especificaciones para las bandas de parada de los filtros.
Diseñe filtros FIR equiripple e IIR Butterworth de orden mínimo con las especificaciones siguientes: banda de paso a partir de [1/40,1/4] ciclos/día y bandas de parada a partir de [0,1/60] y [1/4,1/2] ciclos/día. Establezca ambas atenuaciones de la banda de parada en 10 dB y la tolerancia de ondulación de la banda de paso en 1 dB.
Hd1 = designfilt("bandpassfir", ... StopbandFrequency1=1/60,PassbandFrequency1=1/40, ... PassbandFrequency2=1/4 ,StopbandFrequency2=1/2 , ... StopbandAttenuation1=10,PassbandRipple=1, ... StopbandAttenuation2=10,DesignMethod="equiripple",SampleRate=Fs); Hd2 = designfilt("bandpassiir", ... StopbandFrequency1=1/60,PassbandFrequency1=1/40, ... PassbandFrequency2=1/4 ,StopbandFrequency2=1/2 , ... StopbandAttenuation1=10,PassbandRipple=1, ... StopbandAttenuation2=10,DesignMethod="butter",SampleRate=Fs);
Compare el orden de los filtros FIR e IIR y las respuestas de fase no envuelta.
fprintf("The order of the FIR filter is %d\n",filtord(Hd1))The order of the FIR filter is 78
fprintf("The order of the IIR filter is %d\n",filtord(Hd2))The order of the IIR filter is 8
[phifir,wf] = phasez(Hd1,[],1); [phiiir,wi] = phasez(Hd2,[],1); figure plot(wf,unwrap(phifir)) hold on plot(wi,unwrap(phiiir)) hold off xlabel("Cycles/Day") ylabel("Radians") legend("FIR Equiripple Filter","IIR Butterworth Filter") grid on
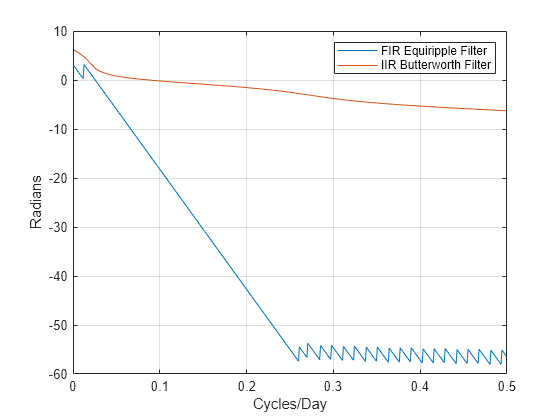
El filtro IIR tiene un orden muy inferior al del filtro FIR. Sin embargo, el filtro FIR tiene una respuesta de fase lineal por encima de la banda de paso, mientras que el filtro IIR no la tiene. El filtro FIR retarda por igual todas las frecuencias de la banda de paso del filtro, mientras que el filtro IIR no lo hace.
Además, la tasa de cambio de la fase por unidad de frecuencia es mayor en el filtro FIR que en el filtro IIR.
Diseñe un filtro FIR equiripple paso bajo para comparar. Las especificaciones de los filtros paso bajo son: banda de paso [0,1/4] ciclos/día, atenuación de la banda de parada igual a 10 B y tolerancia de ondulación de la banda de paso establecida en 1 dB.
Hdlow = designfilt("lowpassfir", ... PassbandFrequency=1/4,StopbandFrequency=1/2, ... PassbandRipple=1,StopbandAttenuation=10, ... DesignMethod="equiripple",SampleRate=1);
Filtre los datos con los filtros paso banda y paso bajo.
yfir = filter(Hd1,y); yiir = filter(Hd2,y); ylow = filter(Hdlow,y);
Represente la estimación de PSD de la salida del filtro IIR paso banda. Puede reemplazar yiir por yfir en el siguiente código para ver la estimación de PSD de la salida del filtro FIR paso banda.
[pxx,f] = periodogram(yiir,[],[],Fs); plot(f,10*log10(pxx)) xlabel("Cycles/day") ylabel("dB") grid on
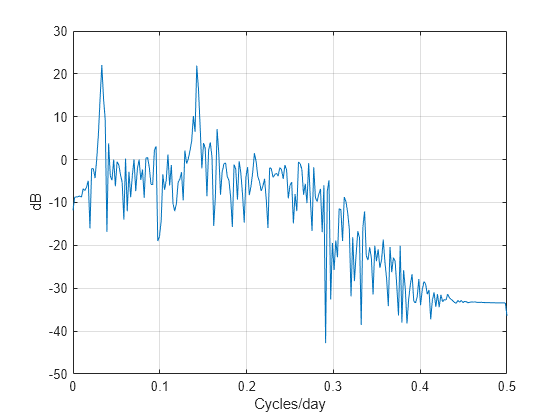
La estimación de PSD muestra que el filtro paso banda atenúa la tendencia de baja frecuencia y el ruido de alta frecuencia.
Represente los primeros 120 días de la salida de los filtros FIR e IIR.
plot(n,yfir,n,yiir) axis([1 120 -2.8 2.8]) xlabel("Days") legend("FIR bandpass filter output", ... "IIR bandpass filter output",Location="SouthEast")
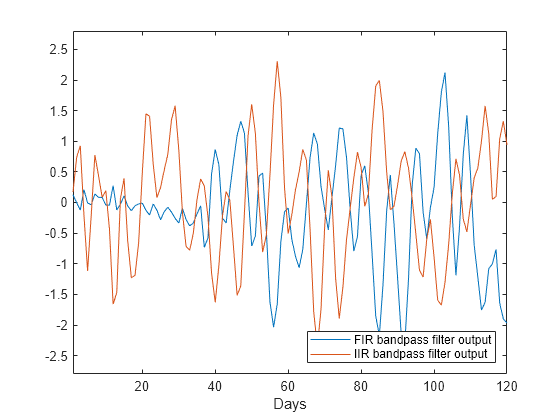
El retardo de fase aumentado en el filtro FIR es evidente en la salida del filtro.
Represente la salida del filtro FIR paso bajo superpuesta en la superposición de los ciclos de 7 y 30 días para comparar.
plot(n,x,n,ylow) xlim([1 365]) xlabel("Days") legend("7-day and 30-day cycles","FIR lowpass filter output", ... Location="NorthWest")
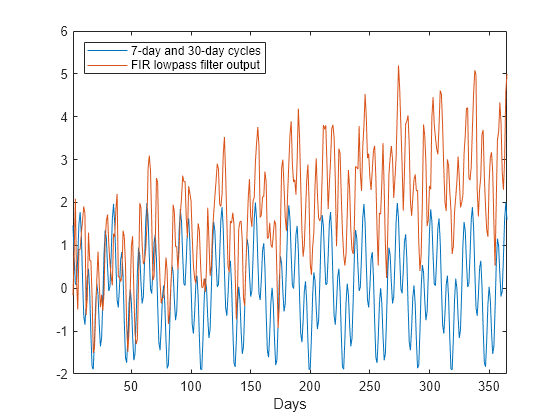
En la gráfica anterior puede ver que la tendencia de baja frecuencia es evidente en la salida del filtro paso bajo. Mientras que el filtro paso bajo mantiene los ciclos de 7 y 30 días, los filtros paso banda funcionan mejor en este ejemplo porque los filtros paso banda también eliminan la tendencia de baja frecuencia.
Filtrado de fase cero
Este ejemplo muestra cómo realizar filtrados de fase cero.
Repita la generación de señal y el diseño de filtro paso bajo con fir1 y designfilt. No tiene que ejecutar el siguiente código si ya tiene estas variables en su área de trabajo.
rng("default") Fs = 1000; t = linspace(0,1,Fs); x = cos(2*pi*100*t)+0.5*randn(size(t)); % Using fir1 fc = 150; Wn = (2/Fs)*fc; b = fir1(20,Wn,"low",kaiser(21,3)); % Using designfilt Hd = designfilt("lowpassfir",FilterOrder=20,CutoffFrequency=150, ... DesignMethod="window",Window={@kaiser,3},SampleRate=Fs);
Filtre los datos utilizando filter. Represente los primeros 100 puntos de la salida del filtro a lo largo de una sinusoide superpuesta con la misma amplitud y la misma fase inicial que la señal de entrada.
yout = filter(Hd,x); xin = cos(2*pi*100*t); plot(t,xin,t,yout) xlim([0 0.1]) xlabel("Time (s)") ylabel("Amplitude") legend("Input Sine Wave","Filtered Data") grid on
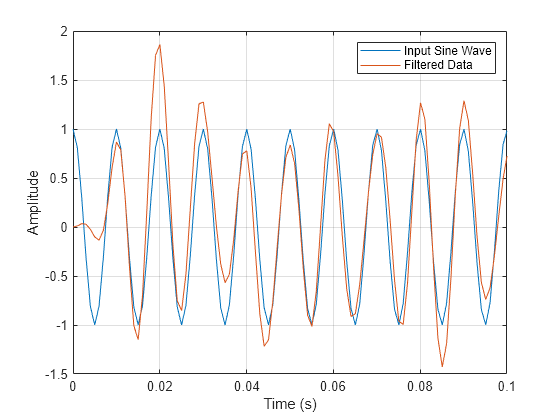
Observando los 0,01 segundos iniciales de los datos filtrados, se ve que la salida está retardada con respecto a la entrada. El retardo parece ser de aproximadamente 0,01 segundos, es decir, casi 1/2 de la longitud del filtro FIR en las muestras .
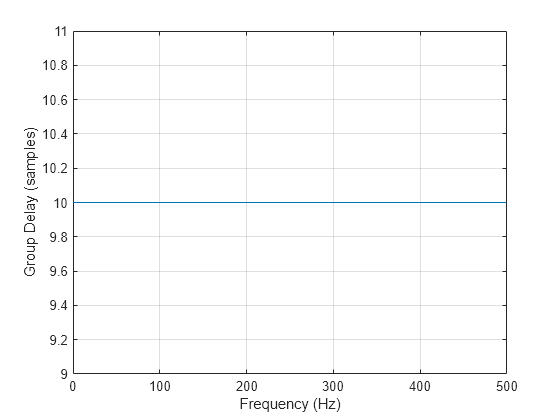
Este retardo se debe a la respuesta de fase del filtro. El filtro FIR de estos ejemplos es un filtro de fase lineal tipo I. El retardo de grupo del filtro es de 10 muestras.
Represente el retardo de grupo.
[gd,f] = grpdelay(Hd,[],Fs); plot(f,gd) xlabel("Frequency (Hz)") ylabel("Group Delay (samples)") grid on
La distorsión de fase es aceptable en muchas aplicaciones. Esto resulta especialmente cierto cuando la respuesta de fase es lineal. En otras aplicaciones es deseable tener un filtro con una respuesta de fase cero. Una respuesta de fase cero no es técnicamente posible en un filtro no causal. Sin embargo, puede implementar un filtrado de fase cero utilizando un filtro causal con filtfilt.
Filtre la señal de entrada utilizando filtfilt. Represente las respuestas para comparar las salidas de filtro obtenidas con filter y filtfilt.
yzp = filtfilt(Hd,x); plot(t,xin,t,yout,t,yzp) xlim([0 0.1]) xlabel("Time (s)") ylabel("Amplitude") legend("100-Hz Sine Wave","Filtered Signal", ... "Zero-phase Filtering",Location="NorthEast")
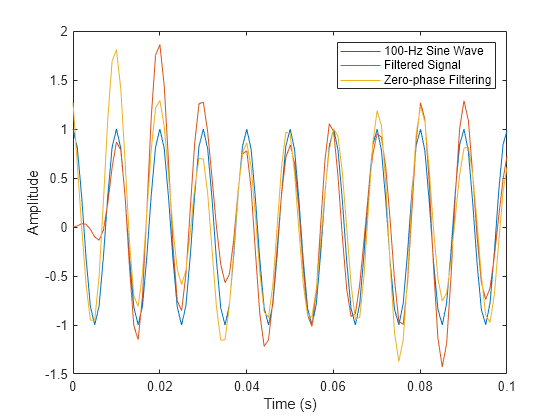
En la figura anterior, puede ver que la salida de filtfilt no presenta el retardo debido a la respuesta de fase del filtro FIR.