Análisis de ceros y polos
La función zplane representa polos y ceros de un sistema lineal. Por ejemplo, un filtro simple con un cero a -1/2 y un par de polos complejos a y es
zer = -0.5; pol = 0.9*exp(j*2*pi*[-0.3 0.3]');
Para ver la gráfica de polos y ceros para este filtro, puede utilizar zplane. Proporcione argumentos de vector columna cuando el sistema esté en formato de polos y ceros.
zplane(zer,pol)
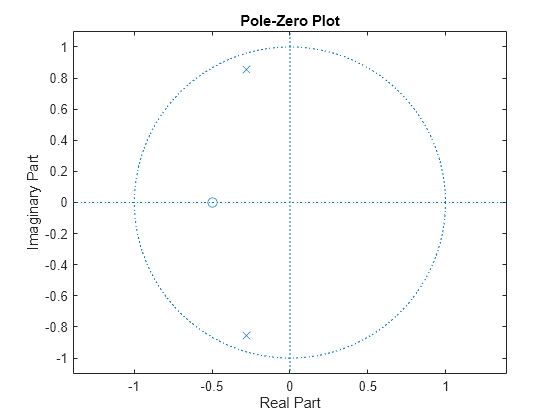
Para utilizar zplane para un sistema en formato de función de transferencia, proporcione argumentos de vector fila. En ese caso, zplane encuentra las raíces del numerador y el denominador utilizando la función roots y representa los ceros y polos resultantes.
[b,a] = zp2tf(zer,pol,1); zplane(b,a)
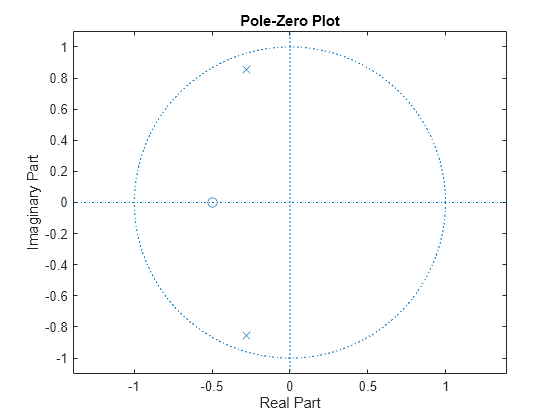
Consulte Modelos de sistemas en tiempo discreto para obtener información sobre la representación de sistemas con ceros y polos y con la función de transferencia.