Battery
Behavioral battery model
Libraries:
Simscape /
Electrical /
Sources
Simscape /
Battery /
Cells
Description
The Battery block represents a simple battery model. You can also expose the charge output port and the thermal port of the battery.
To measure the internal charge level of the battery, in the Main section,
set the Expose charge measurement port to
Yes. This action exposes an extra physical signal port
that outputs the internal state of charge. Use this functionality to change load
behavior as a function of state of charge, without the complexity of building a charge
state estimator.
To simulate the thermal effects of the battery, in the Thermal Port
section, set the Thermal port parameter to
Model. This action exposes an extra thermal port, which
represents the battery thermal mass. When you select this option, provide additional
parameters to define battery behavior at a second temperature. For more information, see
Modeling Thermal Effects.
The battery equivalent circuit is made up of the fundamental battery model, the self-discharge resistance RSD, the charge dynamics model, and the series resistance R0.

Battery Model
If you select Infinite for the Battery charge capacity parameter, the block models the battery as a series resistor and a constant voltage source. If you select Finite for the Battery charge capacity parameter, the block models the battery as a series resistor and a charge-dependent voltage source. In the finite case, the voltage is a function of charge and has the following relationship:
where:
SOC(state-of-charge) is the ratio of current charge to rated battery capacity.V0 is the voltage when the battery is fully charged at no load, as defined by the Nominal voltage, Vnom parameter.
β is a constant that is calculated so that the battery voltage is V1 when the charge is AH1. Specify the voltage V1 and cell capacityAH1 using block parameters. AH1 is the charge when the no-load (open-circuit) voltage is V1, and V1 is less than the nominal voltage.
The equation defines an approximate relationship between voltage and remaining charge. This approximation replicates the increasing rate of voltage drop at low charge values, and ensures that the battery voltage becomes zero when the charge level is zero. The advantage of this model is that it requires few parameters, which are readily available on most datasheets.
Modeling Battery Fade
For battery models with finite battery charge capacity, you can model battery performance deterioration depending on the number of discharge cycles. This deterioration is referred to as battery fade. To enable battery fade, set the Battery fade parameter to Enabled. This setting exposes additional parameters in the Fade section.
The block implements battery fade by scaling certain battery parameter values that you specify in the Main section, depending on the number of completed discharge cycles. The block uses multipliers λAH, λR0, and λV1 on the Cell capacity (Ah rating), Internal resistance, and Voltage V1 when charge is AH1 parameter values, respectively. These multipliers, in turn, depend on the number of discharge cycles:
where:
λAH is the multiplier for battery nominal capacity.
λR0 is the multiplier for battery series resistance.
λV1 is the multiplier for voltage V1.
N is the number of discharge cycles completed.
N0 is the number of full discharge cycles completed before the start of the simulation.
AH is the rated battery capacity in ampere-hours.
i(t) is the instantaneous battery output current.
H(i(t)) is the Heaviside function of the instantaneous battery output current. This function returns 0 if the argument is negative, and 1 if the argument is positive.
Note
The Battery block tracks the current and integrates it over time. The number of discharge cycles completed N increases by 1 every time an equivalent cell discharge capacity is extracted.
The block calculates the coefficients k1, k2, and k3 by substituting the parameter values you provide in the Fade section into these battery equations. For example, the default set of block parameters corresponds to the following coefficient values:
k1 = 1e-2
k2 = 1e-3
k3 = 1e-3
You can also define a starting point for a simulation based on the previous charge-discharge history by using the high-priority variable Discharge cycles. For more information, see Variables.
Modeling Thermal Effects
If you set the Thermal port parameter to
Model, you must provide additional parameters to define
battery behavior at a second temperature. The extended equations for the voltage
when you expose the thermal port are:
where:
T is the battery temperature.
T1 is the nominal measurement temperature.
λV is the parameter temperature dependence coefficient for V0.
λβ is the parameter temperature dependence coefficient for β.
β is calculated in the same way as Battery Model, using the temperature-modified nominal voltage V0T.
The internal series resistance, self-discharge resistance, and any charge-dynamic resistances are also functions of temperature:
where λR is the parameter temperature dependence coefficient.
All the temperature dependence coefficients are determined from the corresponding values you provide at the nominal and second measurement temperatures. If you include charge dynamics in the model, the time constants vary with temperature in the same way.
The battery temperature is determined from a summation of all the ohmic losses included in the model:
where:
Mth is the battery thermal mass.
i corresponds to the ith ohmic loss contributor. Depending on how you have configured the block, the losses include:
Series resistance
Self-discharge resistance
First charge dynamics segment
Second charge dynamics segment
Third charge dynamics segment
Fourth charge dynamics segment
Fifth charge dynamics segment
VT,i is the voltage drop across resistor i.
RT,i is resistor i.
Modeling Charge Dynamics
You can model battery charge dynamics by using the Charge dynamics parameter:
No dynamics— The equivalent circuit contains no parallel RC sections. There is no delay between terminal voltage and internal charging voltage of the battery.One time-constant dynamics— The equivalent circuit contains one parallel RC section. Specify the time constant using the First time constant parameter.Two time-constant dynamics— The equivalent circuit contains two parallel RC sections. Specify the time constants using the First time constant and Second time constant parameters.Three time-constant dynamics— The equivalent circuit contains three parallel RC sections. Specify the time constants using the First time constant, Second time constant, and Third time constant parameters.Four time-constant dynamics— The equivalent circuit contains four parallel RC sections. Specify the time constants using the First time constant, Second time constant, Third time constant, and Fourth time constant parameters.Five time-constant dynamics— The equivalent circuit contains five parallel RC sections. Specify the time constants using the First time constant, Second time constant, Third time constant, Fourth time constant, and Fifth time constant parameters.
This figure shows the equivalent circuit for the block configured with two time-constant dynamics.
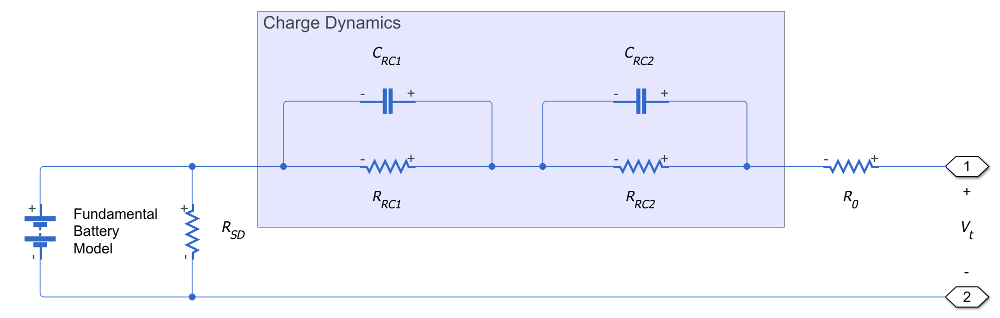
In the diagram:
RRC1 and RRC2 are the parallel RC resistances. Specify these values with the First polarization resistance and Second polarization resistance parameters, respectively.
CRC1 and CRC2 are the parallel RC capacitances. The time constant τ for each parallel section relates the R and C values using the relationship . Specify τ for each section using the First time constant and Second time constant parameters, respectively.
R0 is the series resistance. Specify this value with the Internal resistance parameter.
Modeling Battery Aging
For battery models with finite battery charge capacity, you can model the battery performance deterioration that occurs when the battery is not used. Calendar aging affects both the internal resistance and capacity. In particular, the resistance increase depends by various mechanisms such as the creation of Solid Electrolyte Interface (SEI) at both anode and cathode and the corrosion of the current collector. These processes mainly depend on the storage temperature, the storage state of charge, and time.
Note
The Battery block only applies the calendar aging during
initialization. When you set the Calendar aging parameter
to Enabled, the block exposes the Vector of
time intervals parameter that represents the time the battery has
aged before the start of the simulation. Calendar aging during the simulation is
not covered with this option.
This equation defines the terminal resistance increase of the battery due to calendar aging:
where:
Voc is the Normalized open-circuit voltage during storage, V/Vnom.
R0 is the Internal resistance.
ti is the time sample derived from the Vector of time intervals parameter.
Ti is derived from the Vector of temperatures parameter.
b is the Linear scaling for voltage, b.
c is the Constant offset for voltage, c.
d is the Temperature-dependent exponential increase, d.
a is the Time exponent, a.
q is the electron's elementary charge, in C.
k is the Boltzmann constant, in J/K.
The R1_age_multiplier variable in the Simscape Results Explorer stores the calendar aging of the battery in terms of resistance increase:
For thermal modeling options of the block, if you set the Storage condition parameter to Fixed open-circuit voltage, you must specify the additional Open-circuit voltage measurement temperature parameter to convert the storage open-circuit voltage to the temperature-independent state of charge during storage:
The open-circuit voltage according to the storage temperature is then defined by this equation:
Finally, this equation defines the terminal resistance increase of the battery due to calendar aging according to the storage temperature:
Variables
To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Use nominal values to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources. One of these sources is the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
When you model battery fade, the Discharge cycles variable lets you specify the number of charge-discharge cycles completed prior to the start of simulation. If you disable battery fade modeling, this variable is not used by the block.
Plot Basic Voltage-Charge Characteristics
You can plot the basic voltage-charge characteristics of the Battery block without building a complete model. Use the plots to explore the impact of your parameter choices on device characteristics. If you parameterize the block from a datasheet, you can compare your plots to the datasheet to check that you parameterized the block correctly. If you have a complete working model but do not know which manufactured part to use, you can compare your plots to datasheets to help you decide.
To plot the basic characteristics, right-click the block and select Battery > Basic characteristics from the context menu. For more information about the Basic characteristics option, see Plot Basic Voltage-Charge Characteristics of Battery Blocks.
Assumptions and Limitations
The self-discharge resistance is assumed not to depend strongly on the number of discharge cycles.
For the thermal modeling option of the battery, you provide fade data only for the reference temperature operation. The block applies the same derived λAH, λR0, and λV1 multipliers to parameter values corresponding to the second temperature.
When using the thermal block modeling options, use caution when operating at temperatures outside of the temperature range bounded by the Measurement temperature and Second measurement temperature values. The block uses linear interpolation for the derived equation coefficients, and simulation results can become nonphysical outside of the specified range. The block checks that the internal series resistance, self-discharge resistance, and nominal voltage always remain positive. If there is a violation, the block issues error messages.
Examples
Ports
Output
Conserving
Parameters
References
[1] Ramadass, P., B. Haran, R. E. White, and B. N. Popov. “Mathematical Modeling of the Capacity Fade of Li-Ion Cells.” Journal of Power Sources 123, no. 2 (September 2003): 230–240. https://doi.org/10.1016/S0378-7753(03)00531-7.
[2] Ning, G., B. Haran, and B. N. Popov. “Capacity Fade Study of Lithium-Ion Batteries Cycled at High Discharge Rates.” Journal of Power Sources 117, no. 1-2 (May 2003): 160–169. https://doi.org/10.1016/S0378-7753(03)00029-6.
[3] Schmalstieg, J., S. Käbitz, M. Ecker, and D. U. Sauer. “A Holistic Aging Model for Li(NiMnCo)O2 Based 18650 Lithium-Ion Batteries.” Journal of Power Sources 257 (July 2014): 325–334. https://doi.org/10.1016/j.jpowsour.2014.02.012.


