kmeans
Agrupamiento de k-medias
Sintaxis
Descripción
idx = kmeans(X,k)X en k grupos y devuelve un vector n por 1 (idx) que contiene los índices de grupo de cada observación. Las filas de X se corresponden con los puntos y las columnas se corresponden con variables.
De manera predeterminada, kmeans utiliza la métrica de distancia euclidiana cuadrada y el algoritmo k-medias++ para la inicialización del centro del grupo.
idx = kmeans(X,k,Name,Value)Name,Value.
Por ejemplo, especifique la distancia del coseno, el número de veces que repetir el agrupamiento con nuevos valores iniciales o para utilizar cálculos paralelos.
Ejemplos
Agrupe datos usando el agrupamiento de k-medias y, después, represente las regiones de grupos.
Cargue el conjunto de datos Iris de Fisher. Utilice las longitudes y anchuras de los pétalos como predictores.
load fisheriris X = meas(:,3:4); figure; plot(X(:,1),X(:,2),'k*','MarkerSize',5); title 'Fisher''s Iris Data'; xlabel 'Petal Lengths (cm)'; ylabel 'Petal Widths (cm)';

El mayor grupo parece estar dividido en una región de variaciones menor y otra mayor. Esto podría indicar que el grupo más grande son dos grupos superpuestos.
Agrupe los datos. Especifique k = 3 grupos.
rng(1); % For reproducibility
[idx,C] = kmeans(X,3);idx es un vector de índices de grupos pronosticados que se corresponde con las observaciones en X. C es una matriz 3 por 2 que contiene las ubicaciones finales de los centroides.
Utilice kmeans para calcular la distancia de cada centroide a los puntos en una cuadrícula. Para hacerlo, pase los centroides (C) y los puntos en una cuadrícula a kmeans e implemente una iteración del algoritmo.
x1 = min(X(:,1)):0.01:max(X(:,1)); x2 = min(X(:,2)):0.01:max(X(:,2)); [x1G,x2G] = meshgrid(x1,x2); XGrid = [x1G(:),x2G(:)]; % Defines a fine grid on the plot idx2Region = kmeans(XGrid,3,'MaxIter',1,'Start',C);
Warning: Failed to converge in 1 iterations.
% Assigns each node in the grid to the closest centroidkmeans muestra una advertencia indicando que el algoritmo no ha convergido, lo cual es de esperar ya que el software solo ha implementado una iteración.
Represente las regiones de grupos.
figure; gscatter(XGrid(:,1),XGrid(:,2),idx2Region,... [0,0.75,0.75;0.75,0,0.75;0.75,0.75,0],'..'); hold on; plot(X(:,1),X(:,2),'k*','MarkerSize',5); title 'Fisher''s Iris Data'; xlabel 'Petal Lengths (cm)'; ylabel 'Petal Widths (cm)'; legend('Region 1','Region 2','Region 3','Data','Location','SouthEast'); hold off;

Genere de manera aleatoria los datos de muestra.
rng default; % For reproducibility X = [randn(100,2)*0.75+ones(100,2); randn(100,2)*0.5-ones(100,2)]; figure; plot(X(:,1),X(:,2),'.'); title 'Randomly Generated Data';

Parece que hay dos grupos en los datos.
Divida los datos en dos grupos y seleccione el mejor arreglo de las cinco inicializaciones. Muestre el resultado final.
opts = statset('Display','final'); [idx,C] = kmeans(X,2,'Distance','cityblock',... 'Replicates',5,'Options',opts);
Replicate 1, 3 iterations, total sum of distances = 0.9879171.79822.012450.8117850.42111.476630.935910.7658763.92211.979431.424072.662641.514380.8970231.211160.4900031.413872.344710.9618081.725542.639011.767771.526541.773070.474890.737131.323370.48160.7009451.910930.6884431.523612.030061.231352.433221.058281.000911.655061.244741.553550.3370910.4231971.308820.2056411.31780.8025581.036580.6277072.078681.509511.281030.1702011.127751.479361.012391.006141.158761.246460.3833821.036551.082730.6571421.011252.674342.354170.4094451.978721.251440.9742022.310791.506322.065221.276750.8709761.110391.63371.212310.4582970.5357611.03681.842510.5143450.5416491.19871.261181.256171.22131.371520.6112451.066731.0530.1301640.525781.910790.7818770.722291.450342.043190.5321252.058140.1718340.948870.720610.5322740.5367080.5896830.3956460.534580.5077240.3546260.728470.8935010.4712120.7593141.377580.7991450.6911630.2880741.129630.5508960.9993251.023740.7261060.2204910.9175090.4357990.5026970.2129291.156380.8346460.4969721.187010.5606991.044620.2570.4003661.135382.097341.43670.8821421.192170.5808720.2976160.401890.214231.58420.2424841.005980.4217950.1035350.8210810.1905330.4947271.102361.129220.3802381.103781.424281.211780.6076250.7203680.8542731.048020.5291860.6439461.002930.3392271.094660.1616450.3560030.8847070.6776620.9006650.332320.3368890.8842620.7647690.6776980.9044340.5589671.708050.8172460.3194670.8796910.9693671.099070.8290530.732971.020470.979410.2533961.089880.7817340.9302050.4414340.1001132.052320.634641.114861.52274. Replicate 2, 5 iterations, total sum of distances = 0.9879171.79822.012450.8117850.42111.476630.935910.7658763.92211.979431.424072.662641.514380.8970231.211160.4900031.413872.344710.9618081.725542.639011.767771.526541.773070.474890.737131.323370.48160.7009451.910930.6884431.523612.030061.231352.433221.058281.000911.655061.244741.553550.3370910.4231971.308820.2056411.31780.8025581.036580.6277072.078681.509511.281030.1702011.127751.479361.012391.006141.158761.246460.3833821.036551.082730.6571421.011252.674342.354170.4094451.978721.251440.9742022.310791.506322.065221.276750.8709761.110391.63371.212310.4582970.5357611.03681.842510.5143450.5416491.19871.261181.256171.22131.371520.6112451.066731.0530.1301640.525781.910790.7818770.722291.450342.043190.5321252.058140.1718340.948870.720610.5322740.5367080.5896830.3956460.534580.5077240.3546260.728470.8935010.4712120.7593141.377580.7991450.6911630.2880741.129630.5508960.9993251.023740.7261060.2204910.9175090.4357990.5026970.2129291.156380.8346460.4969721.187010.5606991.044620.2570.4003661.135382.097341.43670.8821421.192170.5808720.2976160.401890.214231.58420.2424841.005980.4217950.1035350.8210810.1905330.4947271.102361.129220.3802381.103781.424281.211780.6076250.7203680.8542731.048020.5291860.6439461.002930.3392271.094660.1616450.3560030.8847070.6776620.9006650.332320.3368890.8842620.7647690.6776980.9044340.5589671.708050.8172460.3194670.8796910.9693671.099070.8290530.732971.020470.979410.2533961.089880.7817340.9302050.4414340.1001132.052320.634641.114861.52274. Replicate 3, 3 iterations, total sum of distances = 0.9879171.79822.012450.8117850.42111.476630.935910.7658763.92211.979431.424072.662641.514380.8970231.211160.4900031.413872.344710.9618081.725542.639011.767771.526541.773070.474890.737131.323370.48160.7009451.910930.6884431.523612.030061.231352.433221.058281.000911.655061.244741.553550.3370910.4231971.308820.2056411.31780.8025581.036580.6277072.078681.509511.281030.1702011.127751.479361.012391.006141.158761.246460.3833821.036551.082730.6571421.011252.674342.354170.4094451.978721.251440.9742022.310791.506322.065221.276750.8709761.110391.63371.212310.4582970.5357611.03681.842510.5143450.5416491.19871.261181.256171.22131.371520.6112451.066731.0530.1301640.525781.910790.7818770.722291.450342.043190.5321252.058140.1718340.948870.720610.5322740.5367080.5896830.3956460.534580.5077240.3546260.728470.8935010.4712120.7593141.377580.7991450.6911630.2880741.129630.5508960.9993251.023740.7261060.2204910.9175090.4357990.5026970.2129291.156380.8346460.4969721.187010.5606991.044620.2570.4003661.135382.097341.43670.8821421.192170.5808720.2976160.401890.214231.58420.2424841.005980.4217950.1035350.8210810.1905330.4947271.102361.129220.3802381.103781.424281.211780.6076250.7203680.8542731.048020.5291860.6439461.002930.3392271.094660.1616450.3560030.8847070.6776620.9006650.332320.3368890.8842620.7647690.6776980.9044340.5589671.708050.8172460.3194670.8796910.9693671.099070.8290530.732971.020470.979410.2533961.089880.7817340.9302050.4414340.1001132.052320.634641.114861.52274. Replicate 4, 3 iterations, total sum of distances = 0.9879171.79822.012450.8117850.42111.476630.935910.7658763.92211.979431.424072.662641.514380.8970231.211160.4900031.413872.344710.9618081.725542.639011.767771.526541.773070.474890.737131.323370.48160.7009451.910930.6884431.523612.030061.231352.433221.058281.000911.655061.244741.553550.3370910.4231971.308820.2056411.31780.8025581.036580.6277072.078681.509511.281030.1702011.127751.479361.012391.006141.158761.246460.3833821.036551.082730.6571421.011252.674342.354170.4094451.978721.251440.9742022.310791.506322.065221.276750.8709761.110391.63371.212310.4582970.5357611.03681.842510.5143450.5416491.19871.261181.256171.22131.371520.6112451.066731.0530.1301640.525781.910790.7818770.722291.450342.043190.5321252.058140.1718340.948870.720610.5322740.5367080.5896830.3956460.534580.5077240.3546260.728470.8935010.4712120.7593141.377580.7991450.6911630.2880741.129630.5508960.9993251.023740.7261060.2204910.9175090.4357990.5026970.2129291.156380.8346460.4969721.187010.5606991.044620.2570.4003661.135382.097341.43670.8821421.192170.5808720.2976160.401890.214231.58420.2424841.005980.4217950.1035350.8210810.1905330.4947271.102361.129220.3802381.103781.424281.211780.6076250.7203680.8542731.048020.5291860.6439461.002930.3392271.094660.1616450.3560030.8847070.6776620.9006650.332320.3368890.8842620.7647690.6776980.9044340.5589671.708050.8172460.3194670.8796910.9693671.099070.8290530.732971.020470.979410.2533961.089880.7817340.9302050.4414340.1001132.052320.634641.114861.52274. Replicate 5, 2 iterations, total sum of distances = 0.9879171.79822.012450.8117850.42111.476630.935910.7658763.92211.979431.424072.662641.514380.8970231.211160.4900031.413872.344710.9618081.725542.639011.767771.526541.773070.474890.737131.323370.48160.7009451.910930.6884431.523612.030061.231352.433221.058281.000911.655061.244741.553550.3370910.4231971.308820.2056411.31780.8025581.036580.6277072.078681.509511.281030.1702011.127751.479361.012391.006141.158761.246460.3833821.036551.082730.6571421.011252.674342.354170.4094451.978721.251440.9742022.310791.506322.065221.276750.8709761.110391.63371.212310.4582970.5357611.03681.842510.5143450.5416491.19871.261181.256171.22131.371520.6112451.066731.0530.1301640.525781.910790.7818770.722291.450342.043190.5321252.058140.1718340.948870.720610.5322740.5367080.5896830.3956460.534580.5077240.3546260.728470.8935010.4712120.7593141.377580.7991450.6911630.2880741.129630.5508960.9993251.023740.7261060.2204910.9175090.4357990.5026970.2129291.156380.8346460.4969721.187010.5606991.044620.2570.4003661.135382.097341.43670.8821421.192170.5808720.2976160.401890.214231.58420.2424841.005980.4217950.1035350.8210810.1905330.4947271.102361.129220.3802381.103781.424281.211780.6076250.7203680.8542731.048020.5291860.6439461.002930.3392271.094660.1616450.3560030.8847070.6776620.9006650.332320.3368890.8842620.7647690.6776980.9044340.5589671.708050.8172460.3194670.8796910.9693671.099070.8290530.732971.020470.979410.2533961.089880.7817340.9302050.4414340.1001132.052320.634641.114861.52274. Best total sum of distances = 201.533
De manera predeterminada, el software inicia las réplicas por separado utilizando k-medias++.
Represente los grupos y sus centroides.
figure; plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12) hold on plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12) plot(C(:,1),C(:,2),'kx',... 'MarkerSize',15,'LineWidth',3) legend('Cluster 1','Cluster 2','Centroids',... 'Location','NW') title 'Cluster Assignments and Centroids' hold off

Se puede determinar la separación de los grupos pasando idx a silhouette.
Agrupar grandes conjuntos de datos puede llevar mucho tiempo, particularmente si utiliza las actualizaciones online (establecidas de manera predeterminada). Si tiene una licencia de Parallel Computing Toolbox™ y establece las opciones para realizar cálculos paralelos, kmeans ejecuta (o replica) cada tarea de agrupamiento en paralelo. Y, si Replicates >1, los cálculos paralelos reducen el tiempo de convergencia.
Genere de manera aleatoria un gran conjunto de datos de un modelo de mezcla gausiano.
rng(1); % For reproducibility Mu = ones(20,30).*(1:20)'; % Gaussian mixture mean rn30 = randn(30,30); Sigma = rn30'*rn30; % Symmetric and positive-definite covariance Mdl = gmdistribution(Mu,Sigma); % Define the Gaussian mixture distribution X = random(Mdl,10000);
Mdl es un modelo gmdistribution de 30 dimensiones con 20 componentes. X es una matriz de datos 10000 por 30 generada de Mdl.
Especifique las opciones de cálculos paralelos.
stream = RandStream('mlfg6331_64'); % Random number stream options = statset('UseParallel',1,'UseSubstreams',1,... 'Streams',stream);
El argumento de entrada 'mlfg6331_64' de RandStream especifica el uso del algoritmo de generación de Fibonacci retardado multiplicativo. options es un arreglo de estructura con campos que especifican opciones para controlar la estimación.
Agrupe los datos usando el agrupamiento de k-medias. Especifique que hay k = 20 grupos en los datos y aumente el número de iteraciones. Típicamente, la función objetivo contiene unos mínimos locales. Especifique 10 réplicas para ayudar a encontrar un mínimo local inferior.
tic; % Start stopwatch timer [idx,C,sumd,D] = kmeans(X,20,'Options',options,'MaxIter',10000,... 'Display','final','Replicates',10);
Starting parallel pool (parpool) using the 'Processes' profile ... 08-Nov-2024 15:52:23: Job Queued. Waiting for parallel pool job with ID 2 to start ... Connected to parallel pool with 4 workers. Replicate 2, 56 iterations, total sum of distances = 7.62036e+06. Replicate 4, 79 iterations, total sum of distances = 7.62412e+06. Replicate 3, 76 iterations, total sum of distances = 7.62583e+06. Replicate 1, 94 iterations, total sum of distances = 7.60746e+06. Replicate 5, 103 iterations, total sum of distances = 7.61753e+06. Replicate 7, 77 iterations, total sum of distances = 7.61939e+06. Replicate 6, 96 iterations, total sum of distances = 7.6258e+06. Replicate 8, 113 iterations, total sum of distances = 7.60741e+06. Replicate 10, 66 iterations, total sum of distances = 7.62582e+06. Replicate 9, 80 iterations, total sum of distances = 7.60592e+06. Best total sum of distances = 7.60592e+06
toc % Terminate stopwatch timerElapsed time is 86.846475 seconds.
La ventana de comandos indica que hay disponibles seis workers. El número de workers puede variar en su sistema. La ventana de comandos muestra el número de iteraciones y el valor de la función objetivo terminal para cada réplica. Los argumentos de salida contienen los resultados de la réplica 9 porque tiene la menor suma total de distancias.
kmeans lleva a cabo agrupamiento de k-medias para dividir datos en k grupos. Cuando tenga un nuevo conjunto de datos que agrupar, puede crear nuevos grupos que incluyan los datos existentes y los nuevos datos utilizando kmeans. La función kmeans es compatible con la generación de código C/C++, de modo que puede generar código que acepte los datos de entrenamiento, devuelva los resultados del agrupamiento y, después, implemente el código en un dispositivo. En este flujo de trabajo, debe pasar los datos de entrenamiento, que pueden tener un tamaño considerable. Para ahorrar memoria en el dispositivo, puede separar el entrenamiento y la predicción por uso de kmeans y pdist2, respectivamente.
Utilice kmeans para crear grupos en MATLAB® y utilice pdist2 en el código generado para asignar nuevos datos a grupos existentes. Para la generación de código, defina una función de punto de entrada que acepte las posiciones de los centroides de los grupos y el nuevo conjunto de datos, y devuelva el índice del grupo más cercano. Después, genere código para la función de punto de entrada.
Generar código C/C++ requiere MATLAB® Coder™.
Llevar a cabo agrupamiento de k-medias
Genere un conjunto de datos de entrenamiento con tres distribuciones.
rng('default') % For reproducibility X = [randn(100,2)*0.75+ones(100,2); randn(100,2)*0.5-ones(100,2); randn(100,2)*0.75];
Divida los datos de entrenamiento en tres grupos con kmeans.
[idx,C] = kmeans(X,3);
Represente los grupos y sus centroides.
figure gscatter(X(:,1),X(:,2),idx,'bgm') hold on plot(C(:,1),C(:,2),'kx') legend('Cluster 1','Cluster 2','Cluster 3','Cluster Centroid')

Asignar nuevos datos a grupos existentes
Genere un conjunto de datos de prueba.
Xtest = [randn(10,2)*0.75+ones(10,2);
randn(10,2)*0.5-ones(10,2);
randn(10,2)*0.75];Clasifique el conjunto de datos de prueba usando los grupos existentes. Encuentre el centroide más cercano de cada punto de datos de prueba con pdist2.
[~,idx_test] = pdist2(C,Xtest,'euclidean','Smallest',1);
Represente los datos de prueba y etiquete los datos de prueba con idx_test utilizando gscatter.
gscatter(Xtest(:,1),Xtest(:,2),idx_test,'bgm','ooo') legend('Cluster 1','Cluster 2','Cluster 3','Cluster Centroid', ... 'Data classified to Cluster 1','Data classified to Cluster 2', ... 'Data classified to Cluster 3')

Generar código
Genere código C que asigne nuevos datos a los grupos existentes. Tenga en cuenta que generar código C/C++ requiere MATLAB® Coder™.
Defina una función de punto de entrada llamada findNearestCentroid que acepte las posiciones de los centroides y nuevos datos, y encuentre el grupo más cercano con pdist2.
Añada la directiva del compilador (o pragma) %#codegen a la función de punto de entrada después de la firma de la función para indicar que intenta generar código para el algoritmo de MATLAB. Añadir esta directiva instruye al analizador de código de MATLAB para ayudarle a diagnosticar y arreglar brechas que provocarían errores durante la generación de código.
type findNearestCentroid % Display contents of findNearestCentroid.m
function idx = findNearestCentroid(C,X) %#codegen [~,idx] = pdist2(C,X,'euclidean','Smallest',1); % Find the nearest centroid
Nota: si hace clic en el botón ubicado en la zona superior derecha de esta página y abre este ejemplo en MATLAB®, MATLAB® abrirá la carpeta de ejemplo. Esta carpeta incluye el archivo de función de punto de entrada.
Genere código mediante codegen (MATLAB Coder). Dado que C y C++ son lenguajes de tipado estático, debe determinar las propiedades de todas las variables de la función de entrada en tiempo de compilación. Para especificar los tipos de datos y el tamaño de arreglo de las entradas de findNearestCentroid, pase una expresión de MATLAB que represente el conjunto de valores con un tipo de datos y un tamaño de arreglo determinado con la opción -args. Para obtener más detalles, consulte Specify Variable-Size Arguments for Code Generation.
codegen findNearestCentroid -args {C,Xtest}
Code generation successful.
codegen genera la función MEX de findNearestCentroid_mex con una extensión dependiente de la plataforma.
Compruebe el código generado.
myIndx = findNearestCentroid(C,Xtest); myIndex_mex = findNearestCentroid_mex(C,Xtest); verifyMEX = isequal(idx_test,myIndx,myIndex_mex)
verifyMEX = logical
1
isequal devuelve una lógica 1 (true), que implica que todas las entradas son iguales. La comparación confirma que la función pdist2, la función findNearestCentroid y la función MEX vuelven al mismo índice.
También puede generar código optimizado CUDA® con GPU Coder™.
cfg = coder.gpuConfig('mex'); codegen -config cfg findNearestCentroid -args {C,Xtest}
Para obtener más información sobre generación de código, consulte General Code Generation Workflow. Para obtener más información sobre GPU coder, consulte Get Started with GPU Coder (GPU Coder) y Supported Functions (GPU Coder).
La función kmeans ignora las filas de tabla que contengan un valor faltante. Para utilizar todas las filas de los datos de entrada para el agrupamiento de k-medias, puede atribuir los valores faltantes usando un modelo de regresión.
Cargue el conjunto de datos carbig y cree una tabla que contenga los predictores Weight, Displacement y Horsepower.
load carbig
X = table(Weight,Displacement,Horsepower);Muestre el número de valores faltantes en cada columna de X.
MissingValues = sum(ismissing(X))
MissingValues = 1×3
0 0 6
La columna 3 (Horsepower) tiene seis valores faltantes. Las otras columnas no contienen valores faltantes.
Entrene un modelo de regresión múltiple usando filas que no contengan valores faltantes. Especifique Horsepower como la variable de respuesta.
HPmodel = fitlm(rmmissing(X),"Horsepower");Muestre una gráfica del modelo de regresión.
plot(HPmodel)
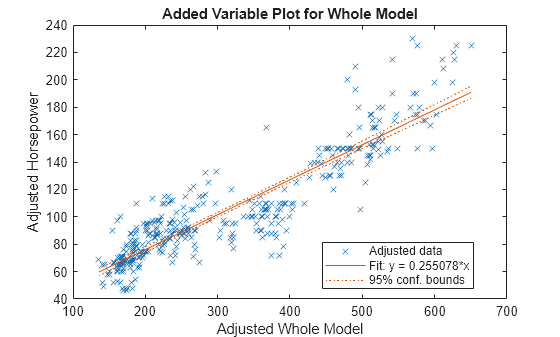
Atribuya los valores de Horsepower faltantes en X usando el modelo de regresión lineal.
imputedHP = predict(HPmodel,X(any(ismissing(X),2),1:2))
imputedHP = 6×1
70.6749
105.0360
65.2328
90.0460
73.9490
94.1612
Sustituya los valores de Horsepower faltantes con los valores atribuidos.
X(any(ismissing(X),2),3) = table(imputedHP);
Agrupe los datos usando el agrupamiento de k-medias. Especifique que los datos tienen tres grupos.
[idx,C] = kmeans(table2array(X),3);
Represente los datos y las asignaciones de grupos.
scatter3(X.Weight,X.Displacement,X.Horsepower,15,idx,"filled")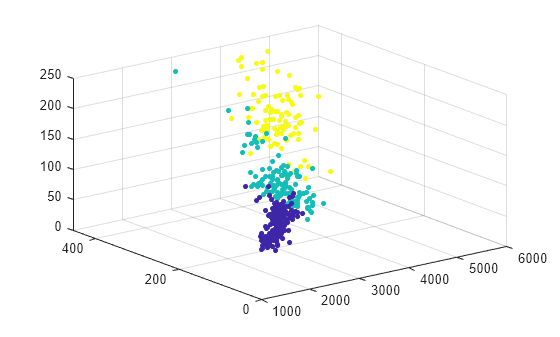
Argumentos de entrada
Datos, especificados como matriz numérica. Las filas de X corresponden a observaciones y las columnas corresponden a variables.
Si X es un vector numérico, kmeans lo trata como una matriz de datos n por 1, independientemente de la orientación.
El software trata NaN en X como datos faltantes y elimina cualquier fila de X que contiene al menos un NaN. Eliminar filas de X reduce el tamaño de la muestra. La función kmeans devuelve NaN para el valor correspondiente en el argumento idx de salida.
Tipos de datos: single | double
Número de grupos en los datos, especificado como un entero positivo.
Tipos de datos: single | double
Argumentos de par nombre-valor
Especifique pares de argumentos opcionales Name1=Value1,...,NameN=ValueN, donde Name es el nombre del argumento y Value es el valor correspondiente. Los argumentos nombre-valor deben aparecer después de otros argumentos, pero el orden de los pares no importa.
En versiones anteriores a R2021a, use comas para separar cada nombre y valor y encierre Name entre comillas.
Ejemplo: 'Distance','cosine','Replicates',10,'Options',statset('UseParallel',1) especifica la distancia del coseno, 10 replica los grupos en diferentes valores iniciales y para utilizar cálculos paralelos.
Nivel de salida que mostrar en la Ventana de comandos, especificado como el par separado por comas que consta de 'Display' y una de las siguientes opciones:
'final': muestra los resultados de la iteración final'iter': muestra los resultados de cada iteración'off': no muestra nada
Cuando especifica 'iter', el software muestra la siguiente información después de cada iteración:
Número de iteración
Fase, donde
1corresponde a la fase de actualización por lotes, y2corresponde a la fase de actualización online (consulte Algoritmos).Número de puntos reasignados a un grupo diferente durante la iteración
Suma de las distancias del punto hasta el centroide del grupo
Ejemplo: 'Display','final'
Métrica de distancia, en espacio p-dimensional, que se utilizó para la minimización, especificada como el par separado por comas que consta de 'Distance' y 'sqeuclidean', 'cityblock', 'cosine', 'correlation' o 'hamming'.
kmeans procesa los grupos del centroide de manera diferente para las métricas de distancia compatibles. La siguiente tabla resume las métricas de distancias disponibles. En cada fórmula, x es una observación (es decir, una fila de X) y c es un centroide (un vector fila).
| Métrica de distancia | Descripción | Fórmula |
|---|---|---|
'sqeuclidean' | Distancia euclidiana cuadrada (valor predeterminado). Cada centroide es la media de puntos en el grupo. |
|
'cityblock' | Suma de las diferencias absolutas, es decir, la distancia L1. Cada centroide es la mediana por componentes de los puntos en un grupo. |
|
'cosine' | Uno menos el coseno del ángulo incluido entre puntos (tratados como vectores). Cada centroide es la media de puntos en el grupo, después de que se normalicen los puntos a la longitud euclidiana unitaria. |
|
'correlation' | Uno menos la correlación de la muestra entre los puntos (tratados como secuencias de valores). Cada centroide es la media por componentes de los puntos en el grupo, después de que los puntos se centren y normalicen a una media de cero y una desviación estándar unitaria. |
donde
|
'hamming' | Esta métrica es solo adecuada para datos binarios. Es la proporción de bits lo que cambia. Cada centroide es la media relacionada con los componentes de puntos en ese grupo. |
en donde I es la función del indicador. |
Ejemplo: 'Distance','cityblock'
Acción a realizar si un grupo pierde todas sus observaciones de miembro, especificada como el par separado por comas que consta de 'EmptyAction' y una de las siguientes opciones.
| Valor | Descripción |
|---|---|
'error' | Trata un grupo vacío como un error. |
'drop' | Elimina cualquier grupo que se queda vacío. |
'singleton' | Crea un nuevo grupo que consta del punto más alejado de su centroide (predeterminado). |
Ejemplo: 'EmptyAction','error'
Número máximo de iteraciones, especificado como el par separado por comas que consta de 'MaxIter' y un entero positivo.
Ejemplo: 'MaxIter',1000
Tipos de datos: double | single
Indicador de actualización online, especificado como el par separado por comas que consta de 'OnlinePhase' y 'off' o 'on'.
Si OnlinePhase es on, kmeans actúa como una fase de actualización online además de una fase de actualización del lote. La fase online puede consumir mucho tiempo para grandes conjuntos de datos, pero garantiza una solución que es un mínimo local del criterio de distancia. En otras palabras, el software encuentra una partición de los datos en la que mover cualquier punto a un grupo diferente aumenta la suma total de distancias.
Ejemplo: 'OnlinePhase','on'
Opciones para controlar el algoritmo iterativo para minimizar los criterios de ajuste, especificado como el par separado por comas que consta de 'Options' y un arreglo de estructura devuelto por statset. Los campos compatibles del arreglo de la estructura especifican las opciones de control del algoritmo iterativo.
Esta tabla resume los campos compatibles. Tenga en cuenta que los campos compatibles precisan Parallel Computing Toolbox™.
| Campo | Descripción |
|---|---|
'Streams' | Un objeto de
En este caso, utilice un arreglo de celdas del mismo tamaño que el grupo paralelo. Si un grupo paralelo no está abierto, |
'UseParallel' |
|
'UseSubstreams' | Establezca el valor en true para calcular de una manera que se pueda reproducir. El valor predeterminado es false. Para calcular de una manera que se pueda reproducir, establezca Streams en un tipo que permita subsecuencias: 'mlfg6331_64' o 'mrg32k3a'. |
Para garantizar unos resultados más predecibles, utilice parpool (Parallel Computing Toolbox) y cree de manera explícita un grupo paralelo antes de invocar kmeans y establecer 'Options',statset('UseParallel',1).
Ejemplo: 'Options',statset('UseParallel',1)
Tipos de datos: struct
Número de veces que repetir el agrupamiento con nuevas posiciones iniciales del centroide del grupo, especificado como el par separado por comas que consta de 'Replicates' y un valor entero. kmeans devuelve la solución con la sumd más baja.
Puede establecer 'Replicates' de manera implícita proporcionando un arreglo 3D como el valor para el argumento de par nombre-valor 'Start'.
Ejemplo: 'Replicates',5
Tipos de datos: double | single
Método para elegir las posiciones iniciales del centroide del grupo (o semillas), especificado como el par separado por comas que consta de 'Start' y 'cluster', 'plus', 'sample', 'uniform', una matriz numérica o un arreglo numérico. Esta tabla resume las opciones disponibles para elegir semillas.
| Valor | Descripción |
|---|---|
'cluster' | Lleva a cabo una fase de agrupamiento preliminar en una submuestra aleatoria del 10% de Si el número de observaciones en la submuestra aleatoria del 10% es menor que |
'plus' (valor predeterminado) | Selecciona k semillas implementando el algoritmo de k-medias++ para la inicialización del centro del grupo. |
'sample' | Selecciona k observaciones de X de manera aleatoria. |
'uniform' | Selecciona k puntos de modo uniforme de manera aleatoria desde el rango de X. No válido con la distancia de Hamming. |
| matriz numérica | Matriz k por p de las ubicaciones iniciales del centroide. Las filas de Start se corresponden con las semillas. El software infiere k de la primera dimensión de Start, para que pueda pasar [] por k. |
| arreglo numérico | Arreglo k por p por r de las ubicaciones iniciales del centroide. Las filas de cada página se corresponden con las semillas. La tercera dimensión invoca la replicación de la rutina de agrupamiento. La página j contiene el conjunto de semillas para replicar j. El software infiere el número de réplicas (especificado por el argumento de par nombre-valor 'Replicates') del tamaño de la tercera dimensión. |
Ejemplo: 'Start','sample'
Tipos de datos: char | string | double | single
Argumentos de salida
Índices de grupo, devueltos como un vector columna numérico. idx tiene tantas filas como X y cada fila indica la asignación de grupo de cada observación correspondiente.
Sumas dentro del grupo de las distancias del punto hasta el centroide, devueltas como un vector columna numérico. sumd es un vector k por 1, donde el elemento j es la suma de las distancias del punto hasta el centro dentro del grupo j. De manera predeterminada, kmeans utiliza la distancia euclidiana cuadrada (consulte las métricas de 'Distance').
Distancias desde cada punto a cada centroide, devueltas como una matriz numérica. D es una matriz n por k, donde el elemento (j,m) es la distancia desde la observación j hasta el centroide m. De manera predeterminada, kmeans utiliza la distancia euclidiana cuadrada (consulte las métricas de 'Distance').
Más acerca de
El agrupamiento de k-medias, o algoritmo de Lloyd [2], es un algoritmo de división de datos iterativo que asigna n observaciones a exactamente uno de k grupos definido por los centroides, donde k se selecciona antes de que comience el algoritmo.
El algoritmo procede de la siguiente manera:
Elige k centros de grupos iniciales (centroide). Por ejemplo, selecciona k observaciones de manera aleatoria (utilizando
'Start','sample') o utiliza el algoritmo de k-medias ++ para la inicialización del centro del grupo (predeterminado).Calcula las distancias del punto hasta el centroide del grupo de todas las observaciones de cada centroide.
Existen dos maneras de proceder (especificadas por
OnlinePhase):Actualización por lotes: asigna cada observación al grupo con el centroide más cercano.
Actualización en línea: asigna de forma individual observaciones a un centroide diferente si la reasignación reduce la suma dentro del grupo, la suma de los cuadrados de las distancias del punto al centroide del grupo.
Para obtener más información, consulte Algoritmos.
Calcula la media de observaciones en cada grupo para obtener k ubicaciones de centroides nuevas.
Repite los pasos 2 a 4 hasta que las asignaciones de grupos no cambien o se alcance el número máximo de iteraciones.
El algoritmo de k-medias++ utiliza una heurística para encontrar las semillas del centroide para el agrupamiento de k-medias. Según Arthur y Vassilvitskii [1], k-medias ++ mejora el tiempo de ejecución del algoritmo de Lloyd y la calidad de la solución final.
El algoritmo de k-medias++ selecciona semillas de la siguiente manera, asumiendo que el número de grupos es k.
Selecciona una observación de manera uniforme aleatoriamente del conjunto de datos, X. La observación elegida es el primer centroide y se indica con c1.
Calcula las distancias de todas las observaciones a c1. Indica la distancias entre cj y la observación de m como .
Selecciona el siguiente centroide, c2 aleatoriamente de X con probabilidad
Para seleccionar el centro j:
Calcula las distancias de cada observación para cada centroide y asigna cada observación a su centroide más cercano.
Para m = 1,...,n y p = 1,...,j – 1, selecciona el centroide j de manera aleatoria de X con probabilidad de
en donde Cp es el conjunto de todas las observaciones más cercanas al centroide cp y xm pertenece a Cp.
Es decir, selecciona cada centro subsiguiente con una probabilidad proporcional a la distancia desde el mismo hasta el centro más cercano que usted ya haya elegido.
Repite el paso 4 hasta que se hayan elegido k centroides.
Arthur y Vassilvitskii [1] demuestran, con un estudio de simulación para varias orientaciones de grupos, que k-medias++ logra una convergencia más rápida para una suma inferior dentro del grupo, la suma de los cuadrados de las distancias del punto hasta el centroide del grupo, que el algoritmo de Lloyd.
Algoritmos
kmeansutiliza un algoritmo iterativo de dos fases para minimizar la suma de las distancias del punto al centroide, sumadas en todos loskgrupos.Esta primera fase utiliza actualizaciones por lotes, donde cada iteración consiste en la reasignación de puntos a su centroide de grupo más cercano, todos a la vez, seguida de un nuevo cálculo de los centroides de los grupos. Esta fase en ocasiones no converge a la solución que es un mínimo local. Es decir, una partición de los datos en la que mover cualquier punto a un grupo diferente aumenta la suma total de distancias. Esto es más probable para los conjuntos de datos pequeños. La fase de lotes es rápida, pero potencialmente solo se aproxima a una solución como punto de partida para la segunda fase.
Esta segunda fase utiliza actualizaciones online, donde los puntos se reasignan de manera individual si haciéndolo se reduce la suma de las distancias y los centroides de los grupos se calculan de nuevo después de cada nueva asignación. Cada iteración de esta fase consiste en una pasada por todos los puntos. Esta fase converge en un mínimo local, aunque puede haber otros mínimos locales con una suma total inferior de las distancias. En general, la búsqueda del mínimo global se resuelve mediante una elección exhaustiva de los puntos iniciales, pero el uso de varias réplicas con puntos de partida aleatorios suele dar como resultado una solución que es un mínimo global.
Si
Replicates= r > 1 yStartesplus(el valor predeterminado), el software selecciona r conjuntos posiblemente diferentes de semillas según el algoritmo k-medias++.Si activa la opción
UseParallelenOptionsyReplicates> 1, entonces cada worker selecciona las semillas y los grupos en paralelo.
Referencias
[1] Arthur, David, and Sergi Vassilvitskii. K-means++: The Advantages of Careful Seeding. In SODA ‘07: Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, 1027–1035. Society for Industrial and Applied Mathematics, 2007.
[2] Lloyd, S. Least Squares Quantization in PCM. IEEE Transactions on Information Theory 28, no. 2 (March 1982): 129–37.
[3] Seber, G. A. F. Multivariate Observations. Hoboken, NJ: John Wiley & Sons, Inc., 1984.
[4] Spath, H. Cluster Dissection and Analysis: Theory, FORTRAN Programs, Examples. Translated by J. Goldschmidt. New York: Halsted Press, 1985.
Capacidades ampliadas
Notas y limitaciones de uso:
Las sintaxis compatibles son:
idx = kmeans(X,k)[idx,C] = kmeans(X,k)[idx,C,sumd] = kmeans(X,k)[___] = kmeans(___,Name,Value)
Los argumentos de par de nombre valor compatibles y cualquier diferencia son:
'Display': el valor predeterminado es'iter'.'MaxIter''Options': admite solo el campo'TolFun'del arreglo de estructura creado porstatset. El valor predeterminado de'TolFun'es1e-4. La funciónkmeansutiliza el valor de'TolFun'como una tolerancia de finalización para las sumas dentro del grupo de las distancias del punto al centroide. Por ejemplo, puede especificar'Options',statset('TolFun',1e-8).'Replicates''Start': solo es compatible con'plus','sample'y un arreglo numérico.
Para obtener más información, consulte Arreglos altos para datos con memoria insuficiente.
Notas y limitaciones de uso:
Si el método
Startutiliza selecciones aleatorias, las posiciones inciales de los centroides de los grupos puede que no coincidan con MATLAB®.Si el número de filas en
Xse fija, la generación de código no elimina las filas deXque contengan unNaN.Las ubicaciones de los centroides de los grupos en
Cpueden tener un orden diferente que en MATLAB. En este caso, los índices de grupos enidxtienen diferencias correspondientes.Si proporciona
Display, su valor debe ser'off'.Si proporciona
Streams, debe estar vacío yUseSubstreamsdebe serfalse.Cuando establece la opción
UseParallelentrue:Algunos cálculos pueden ejecutarse en paralelo incluso cuando
Replicateses1. Para conjuntos de datos grandes, cuandoReplicateses1, considere establecer la opciónUseParallelentrue.kmeansutilizaparfor(MATLAB Coder) para crear bucles que se ejecutan en paralelo en plataformas multinúcleo de memoria compartida ejecutables. Los bucles que se ejecutan en paralelo pueden ser más rápidos que los bucles que se ejecutan en un solo proceso. Si su compilador no es compatible con la interfaz de la aplicación de multiprocesamiento abierto (OpenMP) o desactiva la biblioteca OpenMP, MATLAB Coder™ trata los buclesparforcomo buclesfor. Para encontrar compiladores compatibles, consulte compiladores compatibles.
Para ahorrar memoria en el dispositivo en el que implementa el código generado, puede separar el entrenamiento y la predicción con
kmeansypdist2, respectivamente. Utilicekmeanspara crear grupos en MATLAB y utilicepdist2en el código generado para asignar nuevos datos a grupos existentes. Para la generación de código, defina una función de punto de entrada que acepte las posiciones de los centroides de los grupos y el nuevo conjunto de datos, y devuelva el índice del grupo más cercano. Después, genere código para la función de punto de entrada. Para ver un ejemplo, consulte Asignar nuevos datos a grupos existentes y generar código C/C++.kmeansdevuelve índices de tipo de valor entero (int32) en código C/C++ independiente generado. Por lo tanto, la función permite un soporte de precisión simple más estricto cuando utiliza entradas de precisión simple. Para la generación de código MEX, la función sigue devolviendo índices de precisión doble para igualar el comportamiento de MATLAB.
Para obtener más información sobre la generación de código, consulte Introduction to Code Generation y General Code Generation Workflow.
Para ejecutar en paralelo, especifique el argumento nombre-valor Options en la llamada a esta función y establezca el campo UseParallel de la estructura de opciones en true con statset:
Options=statset(UseParallel=true)
Para obtener más información acerca del cálculo en paralelo, consulte Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Esta función es totalmente compatible con los arreglos de GPU. Para obtener más información, consulte Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Historial de versiones
Introducido antes de R2006a
Consulte también
linkage | clusterdata | incrementalKMeans | silhouette | parpool (Parallel Computing Toolbox) | statset | gmdistribution | kmedoids
Sitios web externos
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)