dgt
Description
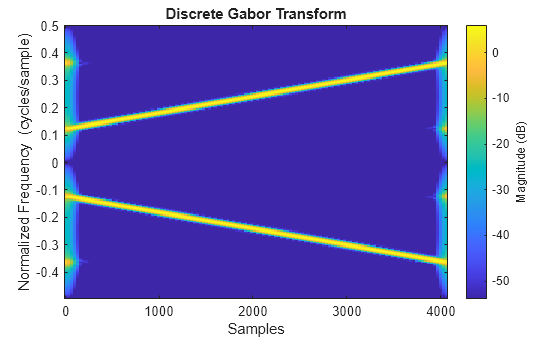
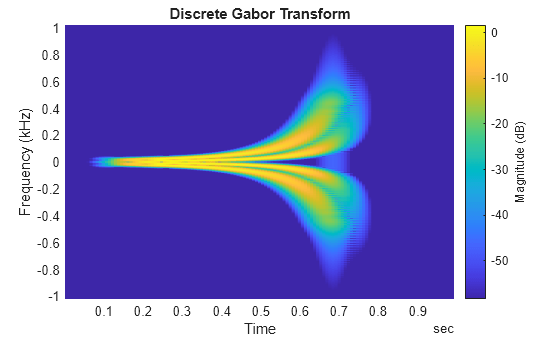
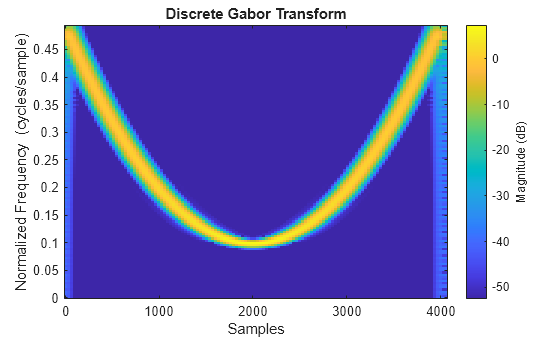
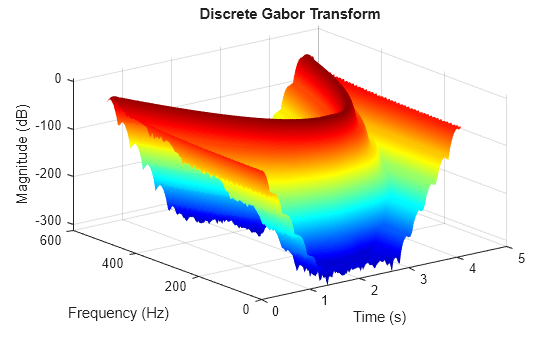
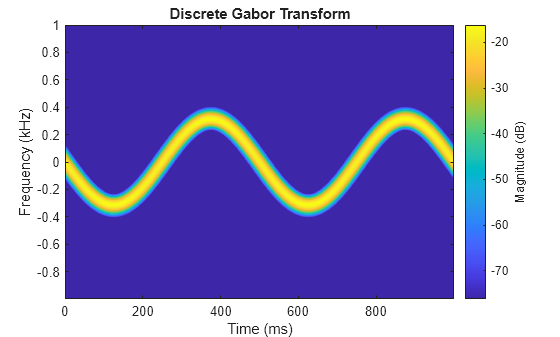
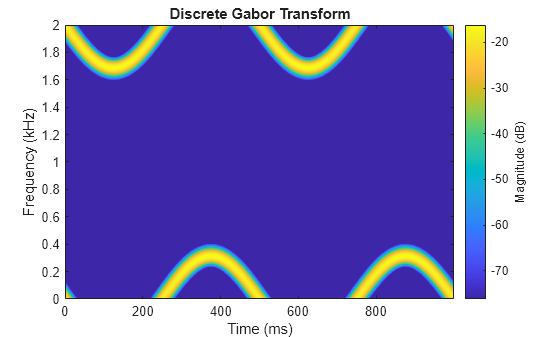
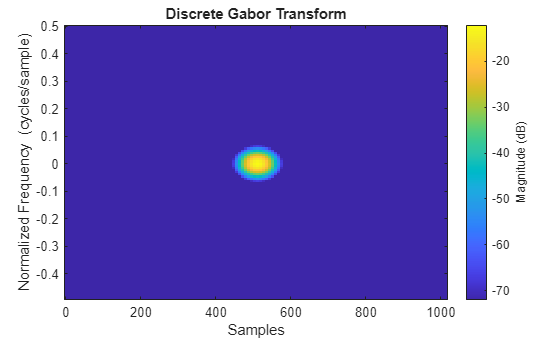
d = dgt(x)x. For more information, see Discrete Gabor Transform.
d = dgt(x,Name=Value)SampleRate to 500.
dgt(___) with no output arguments plots the magnitude
of the DGT in dB in the current figure.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] Qian, S., and D. Chen. “Discrete Gabor Transform.” IEEE Transactions on Signal Processing 41, no. 7 (July 1993): 2429–38. https://doi.org/10.1109/78.224251.
[2] Mallat, S.G. and Zhifeng Zhang. “Matching Pursuits with Time-Frequency Dictionaries.” IEEE Transactions on Signal Processing 41, no. 12 (December 1993): 3397–3415. https://doi.org/10.1109/78.258082.
[3] Søndergaard, Peter. “An Efficient Algorithm for the Discrete Gabor Transform Using Full Length Windows.” In SAMPTA ’09 International Conference on SAMPling Theory and Applications, edited by Laurent Fesquet and Bruno Torresani, 223–26. Marseille, France, 2009. https://hal.science/hal-00495456/file/SampTAProceedings.pdf.
[4] Søndergaard, Peter. “Finite Discrete Gabor Analysis.” Ph.D. Thesis, Technical University of Denmark, 2007. https://orbit.dtu.dk/files/4697157/main.pdf.
Extended Capabilities
Version History
Introduced in R2025a