Esta página se ha traducido mediante traducción automática. Haga clic aquí para ver la última versión en inglés.

dist.

Distancia angular en radianes

Sintaxis

distance = dist(quatA,quatB)

Descripción

distance = dist(quatA,quatB) devuelve la distancia angular en radianes entre dos cuaterniones, quatA y quatB.

Ejemplos

Calcular la distancia del cuaternión

Calcule la distancia del cuaternión entre un solo cuaternión y cada elemento de un vector de cuaterniones. Defina los cuaterniones utilizando los ángulos de Euler.

q = quaternion([0,0,0],"eulerd","ZYX","frame")

q = quaternion
     1 + 0i + 0j + 0k

qArray = quaternion([0,45,0;0,90,0;0,180,0;0,-90,0;0,-45,0],"eulerd","ZYX","frame")

qArray = 5x1 quaternion array
       0.92388 +         0i +   0.38268j +         0k
       0.70711 +         0i +   0.70711j +         0k
    6.1232e-17 +         0i +         1j +         0k
       0.70711 +         0i -   0.70711j +         0k
       0.92388 +         0i -   0.38268j +         0k

quaternionDistance = rad2deg(dist(q,qArray))

quaternionDistance = 5×1

   45.0000
   90.0000
  180.0000
   90.0000
   45.0000

Si ambos argumentos de dist son vectores, la distancia del cuaternión se calcula entre los elementos correspondientes. Calcule la distancia del cuaternión entre dos vectores de cuaternión.

angles1 = [30,0,15; ...
           30,5,15; ...
           30,10,15; ...
           30,15,15];
angles2 = [30,6,15; ...
           31,11,15; ...
           30,16,14; ...
           30.5,21,15.5];

qVector1 = quaternion(angles1,"eulerd","ZYX","frame");
qVector2 = quaternion(angles2,"eulerd","ZYX","frame");

rad2deg(dist(qVector1,qVector2))

ans = 4×1

    6.0000
    6.0827
    6.0827
    6.0287

Tenga en cuenta que un cuaternión representa la misma rotación que su negativo. Calcula un cuaternión y su negativo.

qPositive = quaternion([30,45,-60],"eulerd","ZYX","frame")

qPositive = quaternion
     0.72332 - 0.53198i + 0.20056j +  0.3919k

qNegative = -qPositive

qNegative = quaternion
    -0.72332 + 0.53198i - 0.20056j -  0.3919k

Encuentra la distancia entre el cuaternión y su negativo.

dist(qPositive,qNegative)

ans = 0

Los componentes de un cuaternión pueden verse diferentes de los componentes de su negativo, pero ambas expresiones representan la misma rotación.

Argumentos de entrada

quatA,quatB — Cuaterniones para calcular la distancia entre

quaternion objetos | arreglos de objetos quaternion

Cuaterniones para calcular la distancia entre ellos, especificados como objetos quaternion separados por comas o arreglos de objetos quaternion de cualquier dimensionalidad. quatA y quatB deben tener tamaños compatibles:

• size(quatA) == size(quatB), o

• numel(quatA) == 1, o

• numel(quatB) == 1, o

• si [Adim1,…,AdimN] = size(quatA) y [Bdim1,…,BdimN] = size(quatB), entonces para i = 1:N, ya sea Adimi==Bdimi o Adim==1 o Bdim==1.

  Si uno de los argumentos del cuaternión contiene solo un cuaternión, entonces esta función devuelve las distancias entre ese cuaternión y cada cuaternión en el otro argumento.

Argumentos de salida

distance — Distancia angular (radianes)

escalar numérico | arreglo numérica

Distancia angular en radianes, devuelta como un escalar numérico o un arreglo numérica. Las dimensiones son las máximas de la unión de size(quatA) y size(quatB).

Tipos de datos: single | double

Algoritmos

La función dist devuelve la distancia angular entre dos cuaterniones.

Un cuaternión puede estar definido por un eje (u_b,u_c,u_d) y un ángulo de rotación θ_q: $$q=\cos \left(\raisebox{1ex}{${\theta }_q$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)+\sin \left(\raisebox{1ex}{${\theta }_q$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)\left(u_b\text{i}+u_c\text{j}+u_d\text{k}\right)$$.

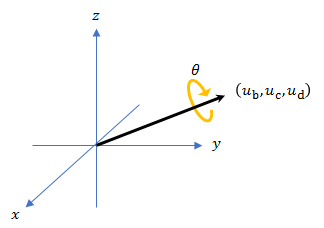
Dado un cuaternión en la forma $$q=a+b\text{i}+c\text{j}+d\text{k}$$, donde a es la parte real, puedes resolver el ángulo de q como $${\theta }_q=2{\cos }^{-1}(a)$$.

Considere dos cuaterniones, p y q, y el producto $$z=p*\text{conjugate}(q)$$. Cuando p se acerca a q, el ángulo de z va a 0, y z se acerca a la unidad. cuaternio.

La distancia angular entre dos cuaterniones se puede expresar como $${\theta }_{\text{z}}=2{\cos }^{-1}\left(\text{real}\left(z\right)\right)$$.

Usando la sintaxis del tipo de datos quaternion , la distancia angular se calcula como:

angularDistance = 2*acos(abs(parts(p*conj(q))));

Capacidades ampliadas

Generación de código C/C++
Genere código C y C++ mediante MATLAB® Coder™.

Historial de versiones

Introducido en R2019b

Consulte también

Funciones

• parts | conj

Objetos

• quaternion

Temas

• Rotaciones, orientación y cuaterniones