Working with Codistributed Arrays
How MATLAB Software Distributes Arrays
When you distribute an array to a number of workers, MATLAB® software partitions the array into segments and assigns one segment of the array to each worker. You can partition a two-dimensional array horizontally, assigning columns of the original array to the different workers, or vertically, by assigning rows. An array with N dimensions can be partitioned along any of its N dimensions. You choose which dimension of the array is to be partitioned by specifying it in the array constructor command.
For example, to distribute an 80-by-1000 array to four workers, you can partition it either by columns, giving each worker an 80-by-250 segment, or by rows, with each worker getting a 20-by-1000 segment. If the array dimension does not divide evenly over the number of workers, MATLAB partitions it as evenly as possible.
The following example creates an 80-by-1000 replicated array and assigns it to
variable A. In doing so, each worker creates an identical array
in its own workspace and assigns it to variable A, where
A is local to that worker. The second command distributes
A, creating a single 80-by-1000 array D
that spans all four workers. Worker 1 stores columns 1 through 250, worker 2 stores
columns 251 through 500, and so on. The default distribution is by the last
nonsingleton dimension, thus, columns in this case of a 2-dimensional array.
spmd
A = zeros(80, 1000);
D = codistributed(A)
end
Worker 1: This worker stores D(:,1:250).
Worker 2: This worker stores D(:,251:500).
Worker 3: This worker stores D(:,501:750).
Worker 4: This worker stores D(:,751:1000).
Each worker has access to all segments of the array. Access to the local segment is faster than to a remote segment, because the latter requires sending and receiving data between workers and thus takes more time.
How MATLAB Displays a Codistributed Array
For each worker, the MATLAB Parallel Command Window displays information about the codistributed array, the local portion, and the codistributor. For example, an 8-by-8 identity matrix codistributed among four workers, with two columns on each worker, displays like this:
>> spmd
II = eye(8,"codistributed")
end
Worker 1:
This worker stores II(:,1:2).
LocalPart: [8x2 double]
Codistributor: [1x1 codistributor1d]
Worker 2:
This worker stores II(:,3:4).
LocalPart: [8x2 double]
Codistributor: [1x1 codistributor1d]
Worker 3:
This worker stores II(:,5:6).
LocalPart: [8x2 double]
Codistributor: [1x1 codistributor1d]
Worker 4:
This worker stores II(:,7:8).
LocalPart: [8x2 double]
Codistributor: [1x1 codistributor1d]To see the actual data in the local segment of the array, use the getLocalPart function.
How Much Is Distributed to Each Worker
In distributing an array of N rows, if N
is evenly divisible by the number of workers, MATLAB stores the same number of rows (N/spmdSize) on
each worker. When this number is not evenly divisible by the number of workers,
MATLAB partitions the array as evenly as possible.
MATLAB provides codistributor object properties called
Dimension and Partition that you
can use to determine the exact distribution of an array. See Indexing into a Codistributed Array for more information on
indexing with codistributed arrays.
Distribution of Other Data Types
You can distribute arrays of any MATLAB built-in data type, and also numeric arrays that are complex or sparse, but not arrays of function handles or object types.
Creating a Codistributed Array
You can create a codistributed array in any of the following ways:
Partitioning a Larger Array — Start with a large array that is replicated on all workers, and partition it so that the pieces are distributed across the workers. This is most useful when you have sufficient memory to store the initial replicated array.
Building from Smaller Arrays — Start with smaller variant or replicated arrays stored on each worker, and combine them so that each array becomes a segment of a larger codistributed array. This method reduces memory requirements as it lets you build a codistributed array from smaller pieces.
Using MATLAB Constructor Functions — Use any of the MATLAB constructor functions like
randorzeroswith a codistributor object argument. These functions offer a quick means of constructing a codistributed array of any size in just one step.
Partitioning a Larger Array
If you have a large array already in memory that you want MATLAB to process more quickly, you can partition it into smaller
segments and distribute these segments to all of the workers using the codistributed function. Each
worker then has an array that is a fraction the size of the original, thus
reducing the time required to access the data that is local to each
worker.
As a simple example, the following line of code creates a 4-by-8 replicated
matrix on each worker assigned to the variable A:
spmd, A = [11:18; 21:28; 31:38; 41:48], end
A =
11 12 13 14 15 16 17 18
21 22 23 24 25 26 27 28
31 32 33 34 35 36 37 38
41 42 43 44 45 46 47 48The next line uses the codistributed function to construct
a single 4-by-8 matrix D that is distributed along the second
dimension of the array:
spmd
D = codistributed(A);
getLocalPart(D)
end
1: Local Part | 2: Local Part | 3: Local Part | 4: Local Part
11 12 | 13 14 | 15 16 | 17 18
21 22 | 23 24 | 25 26 | 27 28
31 32 | 33 34 | 35 36 | 37 38
41 42 | 43 44 | 45 46 | 47 48Arrays A and D are the same size
(4-by-8). Array A exists in its full size on each worker,
while only a segment of array D exists on each worker.
spmd, size(A), size(D), end
Examining the variables in the client workspace, an array that is
codistributed among the workers inside an spmd statement, is
a distributed array from the perspective of the client outside the
spmd statement. Variables that are not codistributed
inside the spmd are Composites in the client outside the spmd.
whos Name Size Bytes Class Attributes A 1x4 489 Composite D 4x8 256 distributed
See the codistributed function
reference page for syntax and usage information.
Building from Smaller Arrays
The codistributed function is less
useful for reducing the amount of memory required to store data when you first
construct the full array in one workspace and then partition it into distributed
segments. To save on memory, you can construct the smaller pieces (local part)
on each worker first, and then use codistributed.build to combine
them into a single array that is distributed across the workers.
This example creates a 4-by-250 variant array A on each of four workers and
then uses codistributor to distribute these segments across
four workers, creating a 16-by-250 codistributed array. Here is the variant
array, A:
spmd
A = [1:250; 251:500; 501:750; 751:1000] + 250 * (spmdIndex - 1);
end
WORKER 1 WORKER 2 WORKER 3
1 2 ... 250 | 251 252 ... 500 | 501 502 ... 750 | etc.
251 252 ... 500 | 501 502 ... 750 | 751 752 ...1000 | etc.
501 502 ... 750 | 751 752 ...1000 | 1001 1002 ...1250 | etc.
751 752 ...1000 | 1001 1002 ...1250 | 1251 1252 ...1500 | etc.
| | |Now combine these segments into an array that is distributed by the first dimension (rows). The array is now 16-by-250, with a 4-by-250 segment residing on each worker:
spmd
D = codistributed.build(A, codistributor1d(1,[4 4 4 4],[16 250]))
end
Worker 1:
This worker stores D(1:4,:).
LocalPart: [4x250 double]
Codistributor: [1x1 codistributor1d]
whos
Name Size Bytes Class Attributes
A 1x4 489 Composite
D 16x250 32000 distributed You could also use replicated arrays in the same fashion, if you wanted to
create a codistributed array whose segments were all identical to start with.
See the codistributed function
reference page for syntax and usage information.
Using MATLAB Constructor Functions
MATLAB provides several array constructor functions that you can use to
build codistributed arrays of specific values, sizes, and classes. These
functions operate in the same way as their nondistributed counterparts in the
MATLAB language, except that they distribute the resultant array across
the workers using the specified codistributor object,
codist.
Constructor Functions. The codistributed constructor functions are listed here. Use the
codist argument (created by the codistributor function:
codist=codistributor()) to specify over which
dimension to distribute the array. See the individual reference pages for
these functions for further syntax and usage information.
eye(___,codist)false(___,codist)Inf(___,codist)NaN(___,codist)ones(___,codist)rand(___,codist)randi(___,codist)randn(___,codist)true(___,codist)zeros(___,codist)codistributed.cell(m,n,...,codist)codistributed.colon(a,d,b) codistributed.linspace(m,n,...,codist) codistributed.logspace(m,n,...,codist)sparse(m,n,codist)codistributed.speye(m,...,codist)codistributed.sprand(m,n,density,codist)codistributed.sprandn(m,n,density,codist)
Local Arrays
That part of a codistributed array that resides on each worker is a piece of a larger array. Each worker can work on its own segment of the common array, or it can make a copy of that segment in a variant or private array of its own. This local copy of a codistributed array segment is called a local array.
Creating Local Arrays from a Codistributed Array
The getLocalPart function copies the segments of a
codistributed array to a separate variant array. This example makes a local copy
L of each segment of codistributed array
D. The size of L shows that it
contains only the local part of D for each worker. Suppose
you distribute an array across four workers:
spmd(4)
A = [1:80; 81:160; 161:240];
D = codistributed(A);
size(D)
L = getLocalPart(D);
size(L)
end
returns on each worker:
3 80 3 20
Each worker recognizes that the codistributed array D is
3-by-80. However, notice that the size of the local part, L,
is 3-by-20 on each worker, because the 80 columns of D are
distributed over four workers.
Creating a Codistributed from Local Arrays
Use the codistributed.build function
to perform the reverse operation. This function, described in Building from Smaller Arrays, combines the
local variant arrays into a single array distributed along the specified
dimension.
Continuing the previous example, take the local variant arrays
L and put them together as segments to build a new
codistributed array X.
spmd codist = codistributor1d(2,[20 20 20 20],[3 80]); X = codistributed.build(L,codist); size(X) end
returns on each worker:
3 80
Obtaining information About the Array
MATLAB offers several functions that provide information on any particular array. In addition to these standard functions, there are also two functions that are useful solely with codistributed arrays.
Determining Whether an Array Is Codistributed
The iscodistributed function
returns a logical 1 (true) if the input
array is codistributed, and logical 0
(false) otherwise. The syntax is
spmd, TF = iscodistributed(D), end
where D is any MATLAB array.
Determining the Dimension of Distribution
The codistributor object determines how an array is partitioned and its
dimension of distribution. To access the codistributor of an array, use the
getCodistributor function.
This returns two properties, Dimension and
Partition:
spmd, getCodistributor(X), end
Dimension: 2
Partition: [20 20 20 20]
The Dimension value of 2 means the array
X is distributed by columns (dimension 2); and the
Partition value of [20 20 20 20] means
that twenty columns reside on each of the four workers.
To get these properties programmatically, return the output of
getCodistributor to a variable, then use dot notation to
access each property:
spmd
C = getCodistributor(X);
part = C.Partition
dim = C.Dimension
endOther Array Functions
Other functions that provide information about standard arrays also work on codistributed arrays and use the same syntax.
Changing the Dimension of Distribution
When constructing an array, you distribute the parts of the array along one of the
array's dimensions. You can change the direction of this distribution on an existing
array using the redistribute function with a different
codistributor object.
Construct an 8-by-16 codistributed array D of random values
distributed by columns on four workers:
spmd
D = rand(8,16,codistributor());
size(getLocalPart(D))
endreturns on each worker:
8 4
Create a new codistributed array distributed by rows from an existing one already distributed by columns:
spmd
X = redistribute(D, codistributor1d(1));
size(getLocalPart(X))
endreturns on each worker:
2 16
Restoring the Full Array
You can restore a codistributed array to its undistributed form using the
gather function.
gather takes the segments of an array that reside on
different workers and combines them into a replicated array on all workers, or into
a single array on one worker.
Distribute a 4-by-10 array to four workers along the second dimension:
spmd, A = [11:20; 21:30; 31:40; 41:50], end
A =
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
spmd, D = codistributed(A), end
WORKER 1 WORKER 2 WORKER 3 WORKER 4
11 12 13 | 14 15 16 | 17 18 | 19 20
21 22 23 | 24 25 26 | 27 28 | 29 30
31 32 33 | 34 35 36 | 37 38 | 39 40
41 42 43 | 44 45 46 | 47 48 | 49 50
| | |
spmd, size(getLocalPart(D)), end
Worker 1:
4 3
Worker 2:
4 3
Worker 3:
4 2
Worker 4:
4 2Restore the undistributed segments to the full array form by gathering the segments:
spmd, X = gather(D), end
X =
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
spmd, size(X), end
4 10Indexing into a Codistributed Array
While indexing into a nondistributed array is fairly straightforward,
codistributed arrays require additional considerations. Each dimension of a
nondistributed array is indexed within a range of 1 to the final subscript, which is
represented in MATLAB by the end keyword. The length of any dimension can
be easily determined using either the size or
length function.
With codistributed arrays, these values are not so easily obtained. For example,
the second segment of an array (that which resides in the workspace of worker 2) has
a starting index that depends on the array distribution. For a 200-by-1000 array
with a default distribution by columns over four workers, the starting index on
worker 2 is 251. For a 1000-by-200 array also distributed by columns, that same
index would be 51. As for the ending index, this is not given by using the
end keyword, as end in this case refers to
the end of the entire array; that is, the last subscript of the final segment. The
length of each segment is also not given by using the length or
size functions, as they only return the length of the entire
array.
The MATLAB
colon operator and end keyword are two of the
basic tools for indexing into nondistributed arrays. For codistributed arrays,
MATLAB provides a version of the colon operator, called
codistributed.colon. This actually is a function, not a
symbolic operator like colon.
Note
When using arrays to index into codistributed arrays, you can use only
replicated or codistributed arrays for indexing. The toolbox does not check to
ensure that the index is replicated, as that would require global
communications. Therefore, the use of unsupported variants (such as spmdIndex) to index into codistributed arrays might create
unexpected results.
Example: Find a Particular Element in a Codistributed Array
Suppose you have a row vector of 1 million elements, distributed among several
workers, and you want to locate its element number 225,000. That is, you want to
know what worker contains this element, and in what position in the local part
of the vector on that worker. The globalIndices function
provides a correlation between the local and global indexing of the
codistributed array.
D = rand(1,1e6,"distributed"); %Distributed by columns
spmd
globalInd = globalIndices(D,2);
pos = find(globalInd == 225e3);
if ~isempty(pos)
fprintf(...
'Element is in position %d on worker %d.\n', pos, spmdIndex);
end
endIf you run this code on a pool of four workers you get this result:
Worker 1: Element is in position 225000 on worker 1.
If you run this code on a pool of five workers you get this result:
Worker 2: Element is in position 25000 on worker 2.
Notice if you use a pool of a different size, the element ends up in a different location on a different worker, but the same code can be used to locate the element.
2-Dimensional Distribution
As an alternative to distributing by a single dimension of rows or columns, you
can distribute a matrix by blocks using '2dbc' or two-dimensional
block-cyclic distribution. Instead of segments that comprise a number of complete
rows or columns of the matrix, the segments of the codistributed array are
2-dimensional square blocks.
For example, consider a simple 8-by-8 matrix with ascending element values. You
can create this array in an spmd statement or communicating
job.
spmd
A = reshape(1:64, 8, 8)
endThe result is the replicated array:
1 9 17 25 33 41 49 57
2 10 18 26 34 42 50 58
3 11 19 27 35 43 51 59
4 12 20 28 36 44 52 60
5 13 21 29 37 45 53 61
6 14 22 30 38 46 54 62
7 15 23 31 39 47 55 63
8 16 24 32 40 48 56 64Suppose you want to distribute this array among four workers, with a 4-by-4 block as the local part on each worker. In this case, the worker grid is a 2-by-2 arrangement of the workers, and the block size is a square of four elements on a side (i.e., each block is a 4-by-4 square). With this information, you can define the codistributor object:
spmd
DIST = codistributor2dbc([2 2], 4);
endNow you can use this codistributor object to distribute the original matrix:
spmd
AA = codistributed(A, DIST)
endThis distributes the array among the workers according to this scheme:
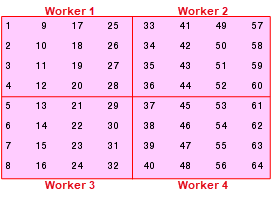
If the worker grid does not perfectly overlay the dimensions of the codistributed
array, you can still use '2dbc' distribution, which is block
cyclic. In this case, you can imagine the worker grid being repeatedly overlaid in
both dimensions until all the original matrix elements are included.
Using the same original 8-by-8 matrix and 2-by-2 worker grid, consider a block size of 3 instead of 4, so that 3-by-3 square blocks are distributed among the workers. The code looks like this:
spmd
DIST = codistributor2dbc([2 2], 3)
AA = codistributed(A, DIST)
endThe first “row” of the worker grid is distributed to worker 1 and worker 2, but that contains only six of the eight columns of the original matrix. Therefore, the next two columns are distributed to worker 1. This process continues until all columns in the first rows are distributed. Then a similar process applies to the rows as you proceed down the matrix, as shown in the following distribution scheme:
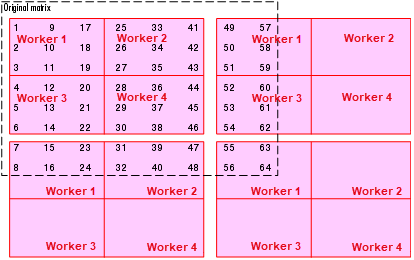
The diagram above shows a scheme that requires four overlays of the worker grid to accommodate the entire original matrix. The following code shows the resulting distribution of data to each of the workers.
spmd
getLocalPart(AA)
endWorker 1:
ans =
1 9 17 49 57
2 10 18 50 58
3 11 19 51 59
7 15 23 55 63
8 16 24 56 64
Worker 2:
ans =
25 33 41
26 34 42
27 35 43
31 39 47
32 40 48
Worker 3:
ans =
4 12 20 52 60
5 13 21 53 61
6 14 22 54 62
Worker 4:
ans =
28 36 44
29 37 45
30 38 46The following points are worth noting:
'2dbc'distribution might not offer any performance enhancement unless the block size is at least a few dozen. The default block size is 64.The worker grid should be as close to a square as possible.
Not all functions that are enhanced to work on
'1d'codistributed arrays work on'2dbc'codistributed arrays.