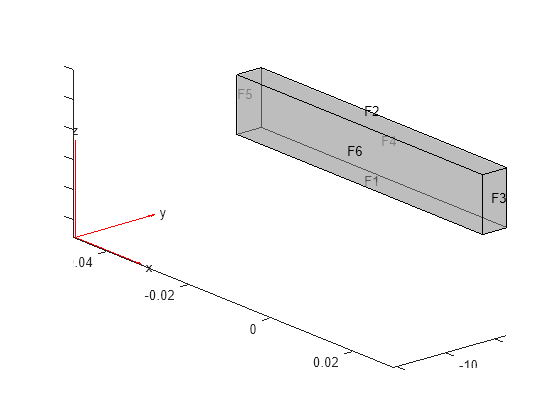
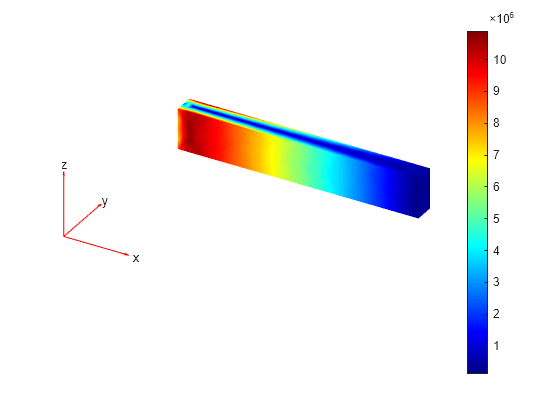
evaluatePrincipalStress
Evaluate principal stress at nodal locations
Description
pStress = evaluatePrincipalStress(structuralresults)structuralresults. For transient and frequency response
structural problems, evaluatePrincipalStress evaluates principal
stress for all time- and frequency-steps, respectively.