Custom PPO Training Loop With Random Network Distillation

This example shows how to train a custom proximal policy optimization (PPO) agent in a custom training loop using a random network distillation (RND) bonus [1]. In the example, you train the PPO agent to swing up and balance a pendulum environment with sparse rewards.

In environments with sparse rewards, it is helpful to use RND to create an exploration reward bonus that guides the agent toward new observations. The RND algorithm randomly initializes two neural networks: a target network that is not updated and a predict network that is updated. The parameters of the predict network ($\theta$) are updated based on gradient descent by minimizing the expected mean squared error (${\mathit{L}}_{\mathrm{RND}}$) between $\widehat{{\mathit{f}}_{\theta }}\left(\mathit{O}\right)$ and $\mathit{f}\left(\mathit{O}\right)$. Here ${\hat{\mathit{f}}}_{\theta }$ is the output of the predict network, ${\mathit{f}}_{}$ is the output of the target network, and $\mathit{O}$ is the observation. This figure shows the networks with their input and outputs.

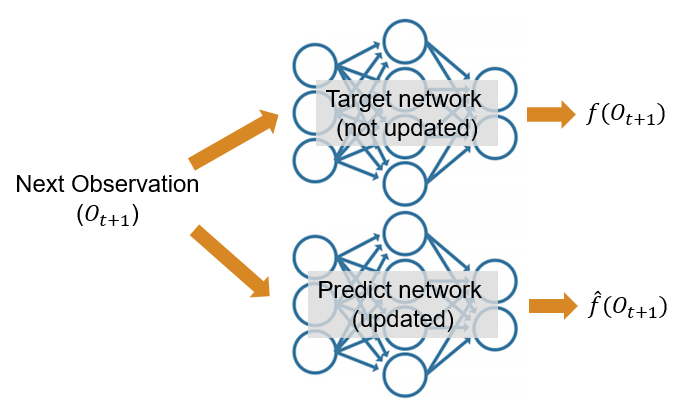
As a consequence of how its parameters are updated, over time, the predict network learns to reproduce the output of the target network.

The agent uses the target and predict networks to compute the reward. Specifically, the total reward is equal to the reward from the environment plus the intrinsic award, where the intrinsic reward is proportional to the squared norm of the difference between the two network outputs

$\mathrm{intrinsic}\mathrm{reward}=\frac{1}{{\mathit{n}}_{\mathit{e}}}||{\hat{\mathit{f}}}_{\theta }\left({\mathit{O}}_{\mathit{t}+1}\right)-\mathit{f}\left({\mathit{O}}_{\mathit{t}+1}\right){||}_2^2$

and where ${\mathit{n}}_{\mathit{e}}$ is the embedding size.

For observations that the agent has seen before, the error and the resulting intrinsic reward are low, because the predict network was trained in that region of the observation space. Conversely, for new observations, the error is larger because the predict network was not trained with the observation, so the intrinsic reward is high. The higher intrinsic rewards promotes exploration in new regions of the observation space, which helps in environments with sparse rewards.

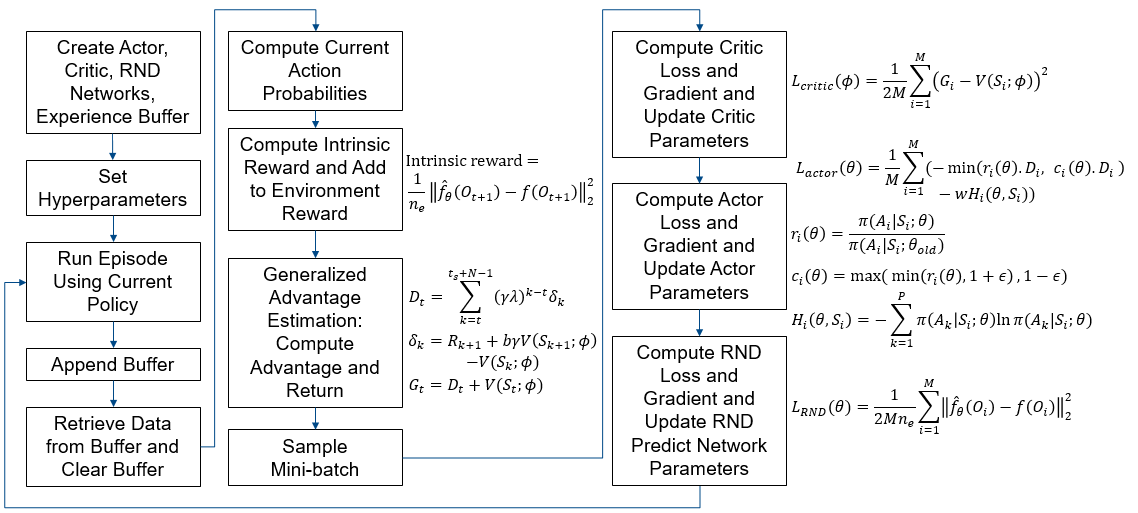
This figure shows the overall process. For more information regarding the PPO training algorithm, refer to Proximal Policy Optimization (PPO) Agent.

Fix Random Number Stream for Reproducibility

The example code might involve computation of random numbers at various stages. Fixing the random number stream at the beginning of various sections in the example code preserves the random number sequence in the section every time you run it, and increases the likelihood of reproducing the results. For more information, see Results Reproducibility.

Fix the random number stream with seed 0 and random number algorithm Mersenne Twister. For more information on controlling the seed used for random number generation, see rng.

previousRngState = rng(0,"twister");

The output previousRngState is a structure that contains information about the previous state of the stream. You will restore the state at the end of the example.

Open Pendulum Swing-Up with Sparse Rewards Model

The reinforcement learning environment for this example is a simple frictionless pendulum that initially hangs in a downward position. The training goal is to make the pendulum stand upright and balanced. The environment is modeled in Simulink®.

Open the model.

mdl = "rlSimplePendulumSparseRewardModel";
open_system(mdl);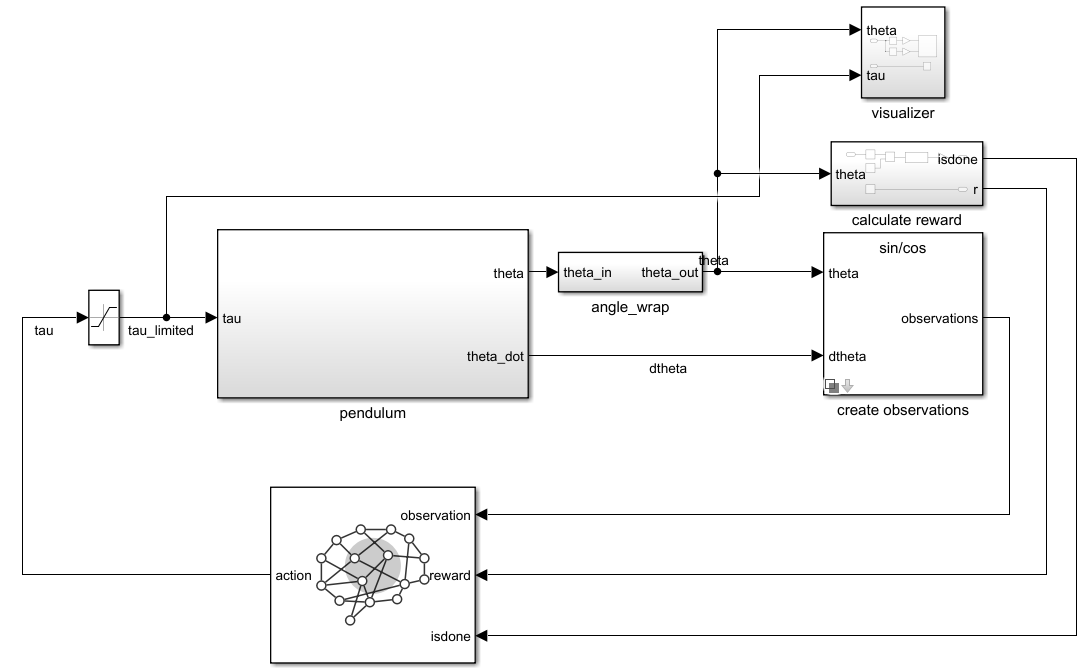

For this model:

• The upward balanced pendulum position is 0 radians, and the downward hanging position is pi radians.

• The torque action signal is discrete from the agent to the environment and can be –2, 0, or 2 N·m.

• The observations from the environment are the sine of the pendulum angle, the cosine of the pendulum angle, and the pendulum angle derivative.

• The reward ${\mathit{r}}_{\mathit{t}}$, provided at every timestep, is

$${\mathit{r}}_{\mathit{t}}=1,\mathrm{if}|{\theta }_{\mathit{t}}|<\frac{\pi }{8}\mathrm{and}0\mathrm{otherwise}.$$

Here, ${\theta }_{\mathit{t}}$ is the angle (counterclockwise-positive) of displacement from the upright position. As you can see, the reward function used here is sparse to show the benefit of using RND in such environments.

For more information on this model, see Load Predefined Control System Environments.

Create Environment Object

Define the observation specification obsInfo and the action specification actInfo.

obsInfo = rlNumericSpec([3 1]);
obsInfo.Name = "Observations";

actInfo = rlFiniteSetSpec([-2 0 2]);
actInfo.Name = "Torque";

Use rlSimulinkEnv to create the environment object.

env = rlSimulinkEnv(mdl,mdl+"/RL Agent",obsInfo,actInfo);

To define the initial condition of the pendulum as hanging downward, specify an environment reset function using an anonymous function handle. This reset function sets the model workspace variable theta0 to pi. For more information on Simulink® environments and their reset functions, see SimulinkEnvWithAgent.

env.ResetFcn = @(in)setVariable(in,"theta0",pi,"Workspace",mdl);

Specify the agent sample time Ts and the simulation time Tf in seconds. Define the maximum number of steps per episode.

Ts = 0.05;
Tf = 20;

Define the maximum number of steps per episode.

maxStepsPerEpisode = ceil(Tf/Ts);

Create Actor, Critic, and Experience Buffer

Ensure reproducibility of the section by fixing the seed used for random number generation.

rng(0,"twister");

Create a critic network and an actor network. The createCriticNet and createActorNet functions are defined at the end of this example.

criticNet = createCriticNet(obsInfo);
actorNet  = createActorNet(obsInfo,actInfo);

Create a critic and an actor. For more information, see rlValueFunction and rlDiscreteCategoricalActor. This example uses the structure agentData to store the critic, the actor, and the agent options and hyperparameters.

agentData.Critic= rlValueFunction(criticNet,obsInfo);
agentData.Actor = rlDiscreteCategoricalActor(actorNet,obsInfo,actInfo);

Use rlOptimizer to create optimizer objects for updating the actor and critic.

• Set the learning rate to 5e-3.

• Set the gradient threshold to 5 to avoid large gradients.

optimizerOpt = rlOptimizerOptions( ...
                 LearnRate = 5e-3, ...
                 GradientThreshold = 5);
agentData.CriticOptimizer = rlOptimizer(optimizerOpt);
agentData.ActorOptimizer = rlOptimizer(optimizerOpt);

Set these agent learning options:

• Set the discount factor to 0.99.

• Use mini-batches of 256 experiences. Large batch sizes typically stabilize training.

• Set the experience horizon to the maximum steps per episode.

• Set MinMiniBatchesForLearning to 10 to collect at least 10*MiniBatchSize experiences before each agent update.

agentData.DiscountFactor = 0.99;
agentData.MiniBatchSize = 256;
agentData.NumEpoch = 3;
agentData.ExperienceHorizon = maxStepsPerEpisode;
agentData.MinMiniBatchesForLearning = 10;
agentData.ActionInfo = actInfo;

Accelerate the loss functions to speed up the gradient computation.

agentData.AccelCriticGrad = dlaccelerate(@criticLoss);
agentData.AccelActorGrad = dlaccelerate(@actorLoss);

Create a replay memory to store the experiences. For more information, see rlReplayMemory.

agentData.Replay = rlReplayMemory(obsInfo,actInfo, ...
    (agentData.MinMiniBatchesForLearning+1)*agentData.MiniBatchSize);

Create RND Networks

Ensure reproducibility of the section by fixing the seed used for random number generation.

rng(0,"twister");

Create two RND networks, a target network and a predict network. The createRndNet function is defined at the end of this example.

% The algorithm does not update the target network.
rndTargetNet = createRndNet(obsInfo);
% The algorithm updates the predict network.
rndPredictNet = createRndNet(obsInfo); 

To store the options for the random networks, create the rndOptions structure. Set the RND network learning options:

• Set the learning rate to 0.001.

• Set the momentum of the optimizer for RND to 0.9.

• Set the weight for the intrinsic reward to 5.

rndOptions.LearnRate = 0.001;
rndOptions.Momentum = 0.9;
rndOptions.IntrinsicRewardWeight = 5;

agentData.RNDOptions = rndOptions;
agentData.RNDTargetNet = rndTargetNet;
agentData.RNDPredictNet = rndPredictNet;
agentData.RNDVelocity = []; % Parameter for the SGDM optimizer
agentData.RNDLoss = NaN;
agentData.MeanIntrinsicReward = NaN;
agentData.RNDNumOfLearnSteps = 0;

Set Up Training and Create Data Logger

Create a file data logger object using the rlDataLogger function. For more information, see rlDataLogger. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true. Change agentData.UseRND to false if you don't want to use RND.

doTraining = false;
agentData.UseRND = true;
useLogger = true;
if useLogger && doTraining
    % Create a file data logger object.
    logger = rlDataLogger();
    % Open a Reinforcement Learning Data Viewer window 
    % to visualize the logged data.
    rlDataViewer(logger); 
    setup(logger);

    agentData.Logger = logger;
end

agentData.UseLogger = useLogger;

agentData.StopTrainingValue = 147;
agentData.AverageReward = 0;
agentData.ScoreAveragingWindowLength = 10;

Run Training Loop

Ensure reproducibility of the section by fixing the seed used for random number generation.

rng(0,"twister");

To train the agent, the custom training loop simulates the agent in the environment for a maximum of maxEpisodes episodes.

maxEpisodes = 5000;

For this custom training loop:

• The runEpisode function simulates the agent in the environment for one episode.

• To speed up training, the CleanupPostSim option is set to false when calling runEpisode. Setting this option to false keeps the model compiled between episodes.

• After the training algorithm collects MinMiniBatchesForLearning*MiniBatchSize experiences over multiple episodes, the algorithm updates the agent and the predict RND network through the stepAgent function defined at the end of this example.

• After all the episodes are complete, the cleanup function cleans up the environment. For more information, see cleanup.

% Store the cumulative rewards of all episodes.
rewardAllEpisodes = zeros(maxEpisodes,1);

% Reset the replay memory.
reset(agentData.Replay);

if doTraining
    % Create the policy object from the actor.
    policy = rlStochasticActorPolicy(agentData.Actor);

    % Set the sampleTime property to make sure that the RL Agent block
    % in the environment Simulink model runs at the desired sample time.
    policy.SampleTime = Ts;
    
    % Number of experiences to collect before updating the RL agent.
    numExperiencesToCollect = ...
          agentData.MinMiniBatchesForLearning*agentData.MiniBatchSize;

    for episodeNumber = 1:maxEpisodes
        
        % Run an episode.
        out = runEpisode(env,policy, ...
                         MaxSteps=maxStepsPerEpisode, ...
                         CleanupPostSim=false);
        
        % Collect the experiences.
        experiences = out.AgentData.Experiences;

        % Append the experiences to the replay used for updating
        % the actor and critic.
        append(agentData.Replay,experiences);

        if agentData.Replay.Length >= numExperiencesToCollect
            % Learn when the agent has collected enough data.
            % The stepAgent function updates the actor, the critic, 
            % and the RND predict network.
            agentData = stepAgent(agentData);

            % Create the policy from the actor.
            policy = rlStochasticActorPolicy(agentData.Actor);
            policy.SampleTime = Ts;

        end
        
        % Collect additional episode information.
        epsInfo = out.AgentData.EpisodeInfo;

        cumRew = epsInfo.CumulativeReward;
        obs0 = epsInfo.InitialObservation;
        v0 = getValue(agentData.Critic,obs0);
        
        % Store the episode cumulative reward.
        rewardAllEpisodes(episodeNumber) = cumRew;

        % Compute the average reward.
        if episodeNumber > agentData.ScoreAveragingWindowLength
            agentData.AverageReward = ...
              mean(rewardAllEpisodes ...
              (episodeNumber- ...
               agentData.ScoreAveragingWindowLength:episodeNumber));
        else
            agentData.AverageReward = ...
                       mean(rewardAllEpisodes(1:episodeNumber));
        end

        % Print the results.
        str1 = "Episode Number" + num2str(episodeNumber) + ", ";
        str2 = "Cumulative Reward = " + num2str(cumRew)  + ", ";
        str3 = "Mean intrinsic reward = " ...
            + num2str(agentData.MeanIntrinsicReward) + ", ";
        str4 = "V0 = " + num2str(v0) + "]\n";
        fprintf(str1 + str2 + str3 + str4);

        % Log data.
        if agentData.UseLogger
            store(agentData.Logger, ...
                "EpisodeReward",cumRew, episodeNumber);
            store(agentData.Logger, ...
                "AverageReward",agentData.AverageReward,episodeNumber);
            if agentData.UseRND
                store(agentData.Logger, ...
                 "MeanIntrinsicReward", ...
                 agentData.MeanIntrinsicReward, ...
                 episodeNumber);
            end
            drawnow();
        end
        
        % Stop the training if the average reward is greater than
        % or equal to the previously defined value.
        if agentData.AverageReward >= agentData.StopTrainingValue
            break;
        end
    end

    % Clean up the environment.
    cleanup(env);

    if agentData.UseRND
        save('trainedPolicyRND.mat','policy');
    end

else

    % Load the trained policy (RND was used).
    load('trainedPolicyRND.mat');

end

Analyze Training Results With and Without RND

To examine the usefulness of using an exploration reward bonus in environments with sparse rewards, run two training sessions. In the first session, train the custom PPO agent with RND. In the second session, do not use RND. The example creates the plots using the logged data and the Reinforcement Learning Data Viewer tool. See rlDataViewer for more information.

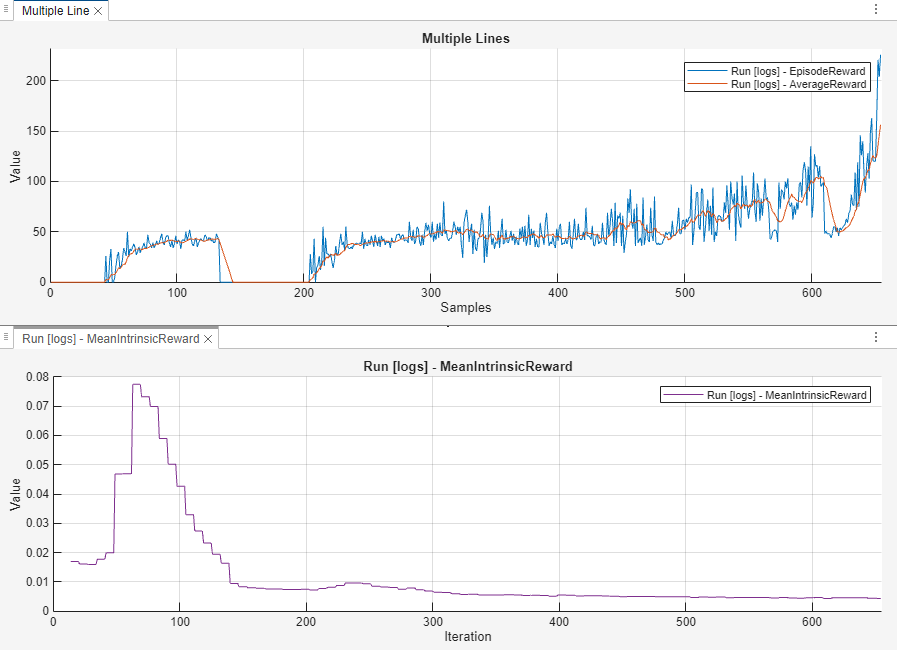
Training With RND

The following plots show the episode reward, average episode reward, and mean intrinsic reward. When the agent trains using RND, the reward is zero for the first 50 episodes but the intrinsic exploration reward bonus is nonzero. This reward bonus encourages the agent to inject more energy in the pendulum and reach the upright sparse reward region of $|{\theta }_{\mathit{t}}|<\frac{\pi }{8}$. After 50 episodes the pendulum starts to reach the upright position. Then both the extrinsic and intrinsic rewards help the agent learn to swing-up and balance the pendulum.

Training Without RND

The following plot shows the episode reward and the average episode reward without using any exploration bonus. The agent does not learn to reach the upright position despite running the training for 5000 episodes. The rewards stay at the same value of zero, because the environment observation never reaches the sparse reward region of ($|{\theta }_{\mathit{t}}|<\frac{\pi }{8}$).

Simulate Trained Policy

Ensure reproducibility of the section by fixing the seed used for random number generation.

rng(0,"twister");

To simulate the trained agent, create a simulation options object and configure it to simulate the environment for 400 steps. For more information on agent simulation, see rlSimulationOptions.

simOptions = rlSimulationOptions("MaxSteps",maxStepsPerEpisode);

% Use the maximum likelihood action (no exploration).
policy.UseMaxLikelihoodAction = true;

Simulate the trained policy. For more information, see sim.

simOut = sim(env,policy,simOptions);

Displaying the cumulative reward obtained by the policy.

sum(simOut(1).Reward)

ans = 
281

The trained policy successfully learned to swing up and balance the pendulum.

Clean up the environment and the logger objects. This operation performs clean up tasks such as writing to file any data still in memory.

cleanup(env);
if useLogger && doTraining
    cleanup(logger);
end

Restore the random number stream using the information stored in previousRngState.

rng(previousRngState);

Agent Step Function

The stepAgent function updates the actor, the critic, and the RND predict network.

function agentData = stepAgent(agentData)
    
    % Get the current critic object.
    currentCritic = agentData.Critic;

    % Generate the experience trajectory.
    allExp = allExperiences(agentData.Replay, ...
        ConcatenateMode="batch",ReturnDlarray=true);
    cln1 = onCleanup(@() reset(agentData.Replay));

    % Generate the action data for the current policy.
    currentActPmf = evaluate(agentData.Actor, ...
        allExp.Observation,UseForward=false);
    
    % Collect experience metrics.
    allExpLen = numel(allExp.Reward);
    eH = agentData.ExperienceHorizon;
    mbLen = agentData.MiniBatchSize;

    % Compute Intrinsic Reward.

    % Ensure the agent was trained at least once.
    if agentData.RNDNumOfLearnSteps>1 
        % Obtain the intrinsic reward as defined
        % in the first section of the example.
        intrinsicReward = rndIntrinsicReward( ...
            agentData.RNDPredictNet, ...
            agentData.RNDTargetNet, allExp.NextObservation);
    
        % Calculate the average intrinsic reward.
        agentData.MeanIntrinsicReward = mean(intrinsicReward);

        % Weight the intrinsic reward and 
        % add it to the environment reward.
        allExp.Reward = allExp.Reward + ...
            agentData.RNDOptions.IntrinsicRewardWeight* ...
            stripdims(intrinsicReward);
    end

    % Compute the advantage against the current critic.
    [advantages,tdTargets] = gaeAdvantage(allExp,currentCritic, ...
        eH,agentData.DiscountFactor,0.95);

    % Loop for the predefined number of epochs.
    for epoch = 1:agentData.NumEpoch

        % Generate the mini-batch indices.
        subTrajIdx = randperm(allExpLen);
        startIdx2 = 1;

        for ii=1:ceil(allExpLen/mbLen)

            % Get the mini-batch indices.
            endIdx2 = min(allExpLen,startIdx2 + mbLen - 1);
            mbIdx = subTrajIdx(startIdx2:endIdx2);
            startIdx2 = endIdx2 + 1;

            % Get the mini-batch data.
            mbObs = {allExp.Observation{:}(:,:,mbIdx)};
            mbNobs = {allExp.NextObservation{:}(:,:,mbIdx)};
            mbAct = {allExp.Action{:}(:,:,mbIdx)};
            mbActPmf = {currentActPmf{:}(:,mbIdx)};
            mbTrg = tdTargets(:,mbIdx);
            mbAdv = advantages(:,mbIdx);

            % Calculate the critic gradient.
            [~,criticGradient] = ...
                dlfeval(agentData.AccelCriticGrad,agentData.Critic, ...
                mbObs,mbTrg);

            % Update the critic.
            [agentData.Critic,agentData.CriticOptimizer] = ...
                update(agentData.CriticOptimizer,agentData.Critic, ...
                criticGradient);

            % actIdx is a matrix containing a one-hot-vector in 
            % each column that indicates which action is selected.
            actIdx = extractdata(squeeze(mbAct{:}))'== ...
                agentData.ActionInfo.Elements;
            
            % Calculate the actor gradient.
            [~,actorGradient] = ...
                dlfeval(agentData.AccelActorGrad,agentData.Actor, ...
                    mbObs,mbActPmf,mbAdv,actIdx);

            % Update the actor.
            [agentData.Actor,agentData.ActorOptimizer] = ...
                update(agentData.ActorOptimizer,agentData.Actor, ...
                actorGradient);
            
            % If you use RND, update the RND networks.
            if agentData.UseRND
                % Calculate the RND gradient for the predict network.
                [agentData.RNDLoss,rndGradient] = dlfeval( ...
                    dlaccelerate(@rndLoss), ...
                    agentData.RNDPredictNet, ...
                    mbNobs, ...
                    agentData.RNDTargetNet);
            
                % Update the predict network parameters 
                % using the SGDM optimizer.
                [agentData.RNDPredictNet,agentData.RNDVelocity] = ...
                    sgdmupdate(agentData.RNDPredictNet, ...
                    rndGradient, ...
                    agentData.RNDVelocity, ...
                    agentData.RNDOptions.LearnRate, ...
                    agentData.RNDOptions.Momentum);

                agentData.RNDNumOfLearnSteps = ...
                    agentData.RNDNumOfLearnSteps+1;
            end

        end
    end
end

Create Critic Network

The createCriticNet function creates a custom network for the critic.

function net = createCriticNet(obsInfo)
    
    numObs = obsInfo.Dimension(1);

    net = [
        featureInputLayer(numObs,Name="obs")
        fullyConnectedLayer(256)
        reluLayer()
        fullyConnectedLayer(256)
        reluLayer()
        fullyConnectedLayer(1,Name="fc_value")
        ];
    net = dlnetwork(net);

end

Create Actor Network

The createActorNet function creates a custom network for the actor.

function net = createActorNet(obsInfo,actInfo)
    
    numObs = obsInfo.Dimension(1);
    numAct = numel(actInfo.Elements);
    
    net = [
        featureInputLayer(numObs,Name="obs")
        fullyConnectedLayer(256)
        reluLayer()
        fullyConnectedLayer(256)
        reluLayer()
        fullyConnectedLayer(numAct,Name="fc_action")
        softmaxLayer(Name="output")
        ];
    
    net = dlnetwork(net);

end

Create RND Network

The createRndNet function creates a RND network.

function net = createRndNet(obsInfo)
    
    numObs = obsInfo.Dimension(1);
    netSize = [128 128];
    numOutputs = 64;

    net = [
        featureInputLayer(numObs,Name="nextobs")
        fullyConnectedLayer(netSize(1),Weights=2/sqrt(numObs)* ...
            (rand(netSize(1),numObs)-0.5), ...
            Bias=2/sqrt(numObs)*(rand(netSize(1),1)-0.5))
        reluLayer()
        fullyConnectedLayer(netSize(2),Weights=2/sqrt(netSize(1))* ...
            (rand(netSize(2),netSize(1))-0.5), ...
        Bias=2/sqrt(netSize(1))*(rand(netSize(2),1)-0.5))
        reluLayer()
        fullyConnectedLayer(numOutputs,Name="fc_act",Weights= ...
            2/sqrt(netSize(2))*(rand(numOutputs,netSize(2))-0.5), ...
            Bias=2/sqrt(netSize(2))*(rand(numOutputs,1)-0.5))
        ];

    net = dlnetwork(net);

end

Compute RND Loss

The rndLoss function computes loss and the gradient to update the RND predict network. This function uses the rndSquaredError function defined below in this example.

function [loss,gradients] = rndLoss( ...
        rndPredictNet,nextObs,rndTargetNet)

    rndSquaredErrorValues = rndSquaredError( ...
        rndPredictNet,rndTargetNet,nextObs,true);

    loss = 0.5.*sum(rndSquaredErrorValues,"all") ...
                /numel(rndSquaredErrorValues);
    gradients = dlgradient(loss,rndPredictNet.Learnables);

end

Get Intrinsic Reward

The rndIntrinsicReward function computes the intrinsic reward by computing the error between the outputs of the target RND network and the predict RND network, given the observation. This function uses the rndSquaredError function defined below in this example.

function intrinsicReward = rndIntrinsicReward( ...
        rndPredictNet,rndTargetNet,nextObs)

    rndSquaredErrorValues = rndSquaredError( ...
        rndPredictNet,rndTargetNet,nextObs,false);
    
    % Calculate the intrinsic reward as explained 
    % in the beginning of the example.
    intrinsicReward = sum( ...
        rndSquaredErrorValues,1)/size(rndSquaredErrorValues, ...
        finddim(rndSquaredErrorValues,'C'));

end

Compute Squared RND Error

The rndSquaredError function computes the squared error by evaluating the RND predict and target networks using the next observation.

function rndSquaredErrorValues = rndSquaredError( ...
        rndPredictNet,rndTargetNet,nextObs,useForward)
    
    % Reshape and format the input data 
    % for featureInputLayer in dlnetwork object.
    formattedObs = dlarray(squeeze(nextObs{:}),"CB");

    % Limit the angle derivative when computing the intrinsic reward.
    % Limiting the angle derivative prevents the agent from increasing 
    % the derivative to gain an exploration bonus that is not useful.
    lowerLimit = -6.5;
    upperLimit = 6.5;
    formattedObs(3,:) = ...
        max(lowerLimit,min(formattedObs(3,:),upperLimit));
    
    if useForward
        [prediction,state] = forward(rndPredictNet,formattedObs);
    else
        [prediction,state] = predict(rndPredictNet,formattedObs);
    end
    [target,state] = predict(rndTargetNet,formattedObs);

    % Compute the squared RND error.
    rndSquaredErrorValues = (prediction - target).^2;

end

Critic Loss

The criticLoss function computes the loss and the gradient to update the critic.

function [loss,dLdP] = criticLoss(critic,obs,target)

    q = getValue(critic,obs,UseForward=true);
    loss = 0.5.*sum((q - target).^2)/numel(q);
    dLdP = dlgradient(loss,critic.Learnables);

end

Actor Loss

The actorLoss function computes the loss and the gradient to update the actor.

function [loss,dLdP] = actorLoss( ...
        actor,obs,currentActPmf,adv,actIdx)

    clipFactor = 0.2;
    entropyW = 0.01;

    % Calculate the new actor probabilities.
    actProbs = evaluate(actor,obs,UseForward=true);

    % Compute the policy ratio from the new policy 
    % against the current policy.
    threshold_ = 1e-8; % using this as threshold
    % Round any values less than threshold_ to threshold_.
    policy_ = actProbs{1}(actIdx);
    policy_(policy_<threshold_) = threshold_;
    previousPolicy_ = currentActPmf{1}(actIdx);
    previousPolicy_(previousPolicy_<threshold_)=threshold_;
    % Calculate the policy ratio.
    policyRatio = exp( log(policy_) - log(previousPolicy_) );
    policyRatio = policyRatio';

    % Compute the (clipped) objective against the advantage.
    objective = adv.*policyRatio;
    clippedObjective = adv.*max(min(policyRatio,1 + clipFactor), ...
                        1 - clipFactor);

    % Compute the advantage loss.
    advantageLoss = -sum(min(objective,clippedObjective),"all");

    % Compute the entropy loss.
    actProbs = actProbs{1};
    actProbs(actProbs<1e-8) = 1e-8;
    entropy_ = sum(-actProbs.*log(actProbs),1);
    entropyLoss = -entropyW*sum(entropy_,"all");

    % Sum the losses.
    loss = (advantageLoss + entropyLoss)/numel(adv);

    % Compute the gradients.
    dLdP = dlgradient(loss,actor.Learnables);

end

Compute GAE Advantage

The gaeAdvantage function computes the GAE advantage. This function uses gaeWeightMatrix and onPolicyValueEstimate, defined as local functions at the end of the example.

function [adv,tdTarget] = gaeAdvantage(trajs,critic,eH,gamma,gaeFactor)

    % Find the end of the episode.
    endOfEpisode = find(extractdata(trajs.IsDone > 0));

    % Calculate the discount weights.
    G = gaeWeightMatrix( ...
        numel(trajs.Reward),eH,gamma*gaeFactor,endOfEpisode);

    sz = size(trajs.Reward);

    % Estimate v and v'.
    [v1,v2] = onPolicyValueEstimate(trajs,critic);

    % Compute the TD error.
    tdErr = trajs.Reward + gamma*v2 - v1;

    % Compute the advantage.
    adv = reshape(tdErr(:)'*G,sz);

    % Compute the TD target.
    tdTarget = adv + v1;

end

GAE Weight Matrix

The gaeWeightMatrix function calculates the discount weights.

function G = gaeWeightMatrix(n,eH,g,endOfEpisode)

    % Treat the last element as endOfEpisode.
    endOfEpisode = unique([endOfEpisode(:);n]);

    % Create the full episode nstep weight matrices.
    P = repmat((0:n-1)',1,n) - (0:n-1);
    G = tril(g.^P);

    % Decouple each experience horizon trajectory.
    m = numel(endOfEpisode);
    horizonStart = 1;
    for i = 1:m
        eoe = endOfEpisode(i);
        while horizonStart <= eoe
            % Find the horizon end (it can be the episode end).
            horizonEnd = min(horizonStart + eH - 1,eoe);
            % Get the indices of all trajectories not part of 
            % this trajectory.
            trajThis  = horizonStart:horizonEnd;
            trajOthers = [(1:(horizonStart-1)),((horizonEnd+1):n)];
            % Decouple only the rows, because G is lower triangular.
            G(trajOthers,trajThis) = 0;
            horizonStart = horizonEnd + 1;
        end
    end

end

On-Policy Value Estimate

The onPolicyValueEstimate function obtains the estimated value from a critic. This function is used by the gaeAdvantage function to calculate the TD error.

function [v1,v2] = onPolicyValueEstimate(trajs,critic)

    isd = trajs.IsDone;

    sz = size(trajs.Reward);

    v1 = reshape(getValue(critic,trajs.Observation),sz);
    v2 = reshape(getValue(critic,trajs.NextObservation),sz);

    v2(isd == 1) = 0;

end

References

[1] Burda, Yuri, Harrison Edwards, Amos Storkey, and Oleg Klimov. "Exploration by Random Network Distillation." arXiv, October 30, 2018. https://arxiv.org/abs/1810.12894.