findsignal
Find signal location using similarity search
Syntax
Description
[
returns the start and stop indices of a segment of the data array,
istart,istop,dist]
= findsignal(data,signal)data, that best matches the search array,
signal. The best-matching segment is such that
dist, the squared Euclidean distance between the
segment and the search array, is smallest. If data and
signal are matrices, then findsignal
finds the start and end columns of the region of data that
best matches signal. In that case,
data and signal must have the same
number of rows.
[ specifies
additional options using name-value pair arguments. Options include
the normalization to apply, the number of segments to report, and
the distance metric to use.istart,istop,dist]
= findsignal(data,signal,Name,Value)
findsignal(___) without output
arguments plots data and highlights any identified
instances of signal.
If the arrays are real vectors, the function displays
dataas a function of sample number.If the arrays are complex vectors, the function displays
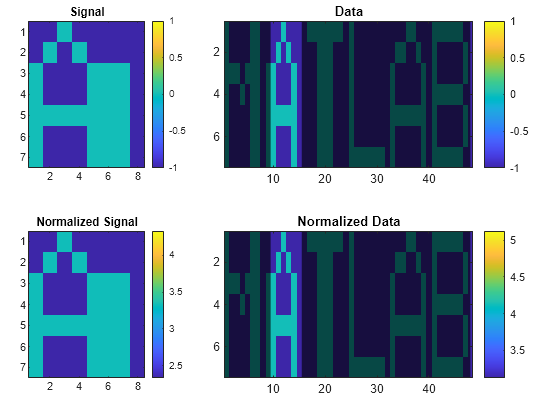
dataon an Argand diagram.If the arrays are real matrices, the function uses
imagescto displaysignalon a subplot anddatawith the highlighted regions on another subplot.If the arrays are complex matrices, the function plots their real and imaginary parts in the top and bottom half of each image.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Extended Capabilities
Version History
Introduced in R2016b