Main Content

La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

hilbert

Señal analítica de tiempo discreto utilizando la transformada de Hilbert

contraer todo en la página

Sintaxis

x = hilbert(xr)
x = hilbert(xr,n)

Descripción

x = hilbert(xr) devuelve la señal analítica, x, de una secuencia de datos real, xr. Si xr es una matriz, hilbert encuentra la señal analítica correspondiente a cada columna.

ejemplo

x = hilbert(xr,n) usa una transformada rápida de Fourier (FFT) de n puntos para calcular la transformada de Hilbert. Los datos de entrada están rellenados con ceros o truncados a la longitud n, según corresponda.

ejemplo

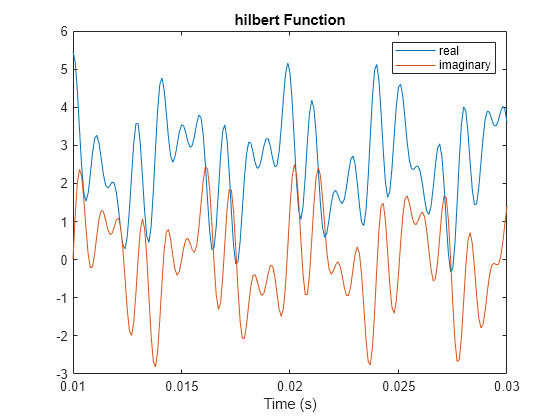
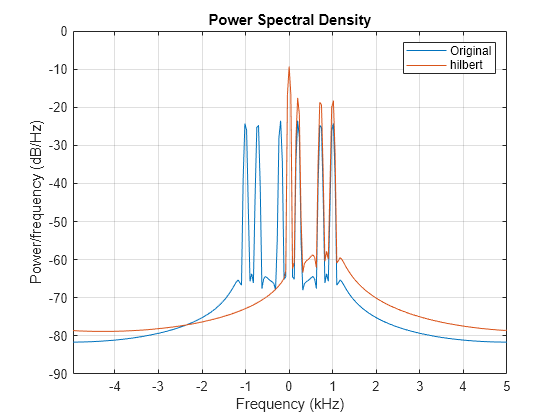
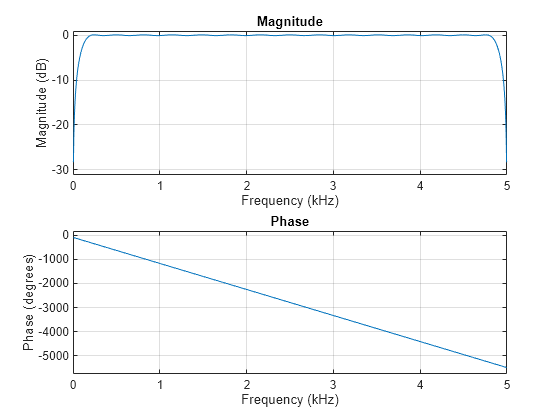
Ejemplos

contraer todo

Abrir script en vivo

Defina una secuencia y calcule su señal analítica mediante hilbert.

xr = [1 2 3 4];
x = hilbert(xr)
x = 1×4 complex

   1.0000 + 1.0000i   2.0000 - 1.0000i   3.0000 - 1.0000i   4.0000 + 1.0000i

La parte imaginaria de x es la transformada de Hilbert de xr y la parte real es la propia xr.

imx = imag(x)
imx = 1×4

     1    -1    -1     1


rex = real(x)
rex = 1×4

     1     2     3     4

La última mitad de la transformada discreta de Fourier (DFT) de x es cero. (En este ejemplo, la última mitad de la transformada es solo el último elemento). Los elementos DC y Nyquist de fft(x) son puramente reales.

dft = fft(x)
dft = 1×4 complex

  10.0000 + 0.0000i  -4.0000 + 4.0000i  -2.0000 + 0.0000i   0.0000 + 0.0000i
Abrir script en vivo

La función hilbert encuentra la señal analítica exacta para un bloque finito de datos. También se puede generar la señal analítica utilizando un filtro transformador de Hilbert con respuesta al impulso finita (FIR) para calcular una aproximación a la parte imaginaria.

Genere una secuencia compuesta por tres sinusoides con frecuencias de 203, 721 y 1001 Hz. La secuencia se muestrea a 10 kHz durante aproximadamente 1 segundo. Utilice la función hilbert para calcular la señal analítica. Represéntela entre 0,01 segundos y 0,03 segundos.

fs = 1e4;
t = 0:1/fs:1; 

x = 2.5 + cos(2*pi*203*t) + sin(2*pi*721*t) + cos(2*pi*1001*t);

y = hilbert(x);

plot(t,real(y),t,imag(y))
xlim([0.01 0.03])
legend('real','imaginary')
title('hilbert Function')
xlabel('Time (s)')

Calcule las estimaciones de Welch de las densidades espectrales de potencia de la secuencia original y de la señal analítica. Divida las secuencias en secciones no solapadas de Hamming de longitud 256. Compruebe que la señal analítica no tiene potencia en las frecuencias negativas.

pwelch([x;y].',256,0,[],fs,'centered')
legend('Original','hilbert')

Utilice la función designfilt para diseñar un filtro transformador de Hilbert con FIR de 60.º orden. Especifique un ancho de transición de 400 Hz. Visualice la respuesta en frecuencia del filtro.

fo = 60;

d = designfilt('hilbertfir','FilterOrder',fo, ...
       'TransitionWidth',400,'SampleRate',fs); 

freqz(d,1024,fs)

Filtre la secuencia sinusoidal para aproximar la parte imaginaria de la señal analítica.

hb = filter(d,x);

El retardo de grupo del filtro, grd, es igual a la mitad del orden del filtro. Compense dicho retardo. Elimine las primeras muestras grd de la parte imaginaria y las últimas muestras grd de la parte real y del vector temporal. Represente el resultado entre 0,01 segundos y 0,03 segundos.

grd = fo/2;
   
y2 = x(1:end-grd) + 1j*hb(grd+1:end);
t2 = t(1:end-grd);

plot(t2,real(y2),t2,imag(y2))
xlim([0.01 0.03])
legend('real','imaginary')
title('FIR Filter')
xlabel('Time (s)')

Calcule la densidad espectral de potencia (PSD) de la señal analítica aproximada y compárela con el resultado hilbert.

pwelch([y;[y2 zeros(1,grd)]].',256,0,[],fs,'centered')
legend('hilbert','FIR Filter')

Argumentos de entrada

contraer todo

Señal de entrada, especificada como un vector o matriz de valor real. Si xr es compleja, hilbert ignora su parte imaginaria.

Ejemplo: sin(2*pi*(0:15)/16) especifica un periodo de una sinusoide.

Ejemplo: sin(2*pi*(0:15)'./[16 8]) especifica una señal sinusoidal de dos canales.

Tipos de datos: single | double

Longitud de la DFT, especificada como escalar entero positivo.

Tipos de datos: single | double

Argumentos de salida

contraer todo

Señal analítica, devuelta como vector o matriz.

Más acerca de

contraer todo

Señal analítica

hilbert devuelve una secuencia helicoidal compleja, en ocasiones llamada señal analítica, de una secuencia de datos real.

La señal analítica x = xr + jxi tiene una parte real, xr, que son los datos originales, y una parte imaginaria, xi, que contiene la transformada de Hilbert. La parte imaginaria es una versión de la secuencia real original con un cambio de fase de 90°. Así, los senos se convierten en cosenos y, de forma análoga, los cosenos se convierten en senos. La serie transformada mediante Hilbert tiene el mismo contenido de amplitud y frecuencia que la secuencia original. La transformada incluye información de fase que depende de la fase de la original.

La transformada de Hilbert es útil para calcular atributos instantáneos de una serie de tiempo, especialmente la amplitud y la frecuencia. La amplitud instantánea es la amplitud de la transformada compleja de Hilbert; la frecuencia instantánea es la tasa de tiempo del cambio del ángulo de fase instantáneo. Para una sinusoide pura, la amplitud y frecuencia instantáneas son constantes. No obstante, la fase instantánea es una sierra, lo que refleja cómo el ángulo de fase local varía linealmente en un solo ciclo. Para mezclas de sinusoides, los atributos son medias a corto plazo o locales que abarcan solo dos o tres puntos. Para ver ejemplos, consulte Transformada de Hilbert y frecuencia instantánea.

La referencia [1] describe el método de Kolmogorov para reconstrucción de fase mínima, que implica tomar la transformada de Hilbert del logaritmo de la densidad espectral de una serie de tiempo. La función de la toolbox rceps realiza esta reconstrucción.

Algoritmos

La señal analítica para una secuencia xr tiene una transformada unilateral de Fourier. Es decir, la transformada desaparece para frecuencias negativas. Para aproximar la señal analítica, hilbert calcula la FFT de la secuencia de entrada, sustituye por ceros los coeficientes de la FFT que corresponden a frecuencias negativas y calcula la FFT inversa del resultado.

hilbert utiliza un algoritmo de cuatro pasos:

  1. Calcule la FFT de la secuencia de entrada y almacene el resultado en un vector x.

  2. Cree un vector h cuyos elementos h(i) tengan los valores:

    • 1 para i = 1, (n/2)+1

    • 2 para i = 2, 3, … , (n/2)

    • 0 para i = (n/2)+2, … , n

  3. Calcule el producto a nivel de elemento de x y h.

  4. Calcule la FFT inversa de la secuencia obtenida en el paso 3 y devuelva los primeros n elementos del resultado.

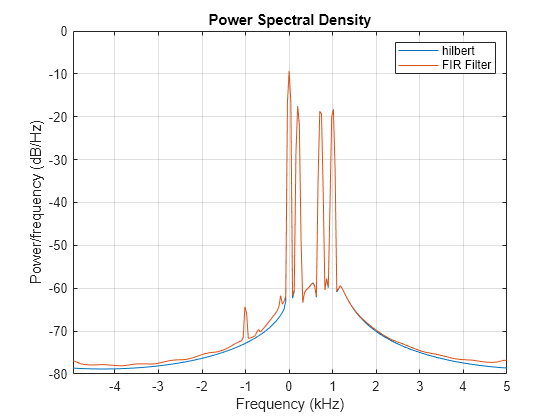
Este algoritmo se introdujo por primera vez en [2]. La técnica asume que la señal de entrada, x, es un bloque finito de datos. Esta suposición permite a la función eliminar la redundancia espectral en x de forma exacta. Los métodos basados en filtrado FIR solo pueden aproximar la señal analítica, pero tienen la ventaja de que operan de forma continua en los datos. Consulte Single-Sideband Amplitude Modulation para ver otro ejemplo de una transformada de Hilbert calculada con un filtro FIR.

Referencias

[1] Claerbout, Jon F. Fundamentals of Geophysical Data Processing with Applications to Petroleum Prospecting. Oxford, UK: Blackwell, 1985.

[2] Marple, S. L. “Computing the Discrete-Time Analytic Signal via FFT.” IEEE® Transactions on Signal Processing. Vol. 47, 1999, pp. 2600–2603.

[3] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. 2nd Ed. Upper Saddle River, NJ: Prentice Hall, 1999.

Capacidades ampliadas

Generación de código C/C++
Genere código C y C++ mediante MATLAB® Coder™.

Generación de código de GPU
Genere código CUDA® para GPU NVIDIA® mediante GPU Coder™.

Historial de versiones

Introducido antes de R2006a

expandir todo

Consulte también

| |