spectrogram
Espectrograma utilizando la transformada de Fourier de tiempo corto
Sintaxis
Descripción
s = spectrogram(x)x. Cada columna de s contiene una estimación del contenido de la frecuencia de tiempo corto localizada en el tiempo de x. La magnitud al cuadrado de s se conoce como la representación de tiempo-frecuencia del espectrograma de x [1].
[ devuelve un vector de frecuencias cíclicas, s,f,t] = spectrogram(___,fs)f, expresado en términos de la tasa de muestreo fs. fs debe ser la quinta entrada para spectrogram. Para introducir una tasa de muestreo y seguir utilizando los valores predeterminados de los argumentos opcionales anteriores, especifique estos argumentos como vacíos, [].
[___, también devuelve una matriz, ps] = spectrogram(___,spectrumtype)ps, proporcional al espectrograma de x.
Si se especifica
spectrumtypecomo"psd", cada columna depscontiene una estimación de la densidad espectral de potencia (PSD) de un segmento con ventana.Si se especifica
spectrumtypecomo"power", cada columna depscontiene una estimación del espectro de potencia de un segmento con ventana.
[___] = spectrogram(___,"reassigned") reasigna cada estimación de la PSD o del espectro de potencia a la ubicación de su centro de energía. Si su señal contiene componentes temporales o espectrales bien ubicados, esta opción genera un espectrograma más nítido.
[___] = spectrogram(___, devuelve la estimación de la PSD o del espectro de potencia a lo largo del rango de frecuencia especificado por freqrange)freqrange. Las opciones válidas para freqrange son "onesided", "twosided" y "centered".
[___] = spectrogram(___, especifica opciones adicionales con argumentos de par nombre-valor. Las opciones incluyen el umbral mínimo y la dimensión de tiempo de salida.Name=Value)
Ejemplos
Genere muestras de una señal que consista en una suma de sinusoides. Las frecuencias normalizadas de las sinusoides son rad/muestra y rad/muestra. La sinusoide de frecuencia superior tiene 10 veces la amplitud de la otra sinusoide.
N = 1024; n = 0:N-1; w0 = 2*pi/5; x = sin(w0*n)+10*sin(2*w0*n);
Calcule la transformada de Fourier de tiempo corto utilizando los valores predeterminados de la función. Represente el espectrograma.
s = spectrogram(x);
spectrogram(x,'yaxis')
Repita el cálculo.
Divida la señal en secciones de longitud .
Disponga en ventanas las secciones utilizando una ventana Hamming.
Especifique el 50% de solapamiento entre las secciones contiguas.
Para calcular la FFT, utilice puntos, donde .
Verifique que los dos enfoques dan resultados idénticos.
Nx = length(x); nsc = floor(Nx/4.5); nov = floor(nsc/2); nff = max(256,2^nextpow2(nsc)); t = spectrogram(x,hamming(nsc),nov,nff); maxerr = max(abs(abs(t(:))-abs(s(:))))
maxerr = 0
Divida la señal en ocho secciones de igual longitud, con un 50% de solapamiento entre las secciones. Especifique la misma longitud de FFT que en el paso anterior. Calcule la transformada de Fourier de tiempo corto y verifique que ofrece el mismo resultado que los dos procedimientos anteriores.
ns = 8; ov = 0.5; lsc = floor(Nx/(ns-(ns-1)*ov)); t = spectrogram(x,lsc,floor(ov*lsc),nff); maxerr = max(abs(abs(t(:))-abs(s(:))))
maxerr = 0
Genere una señal compuesta por un chirp cuadrático convexo de valor complejo muestreado a 600 Hz durante 2 segundos. El chirp tiene una frecuencia inicial de 250 Hz y una final de 50 Hz.
fs = 6e2; ts = 0:1/fs:2; x = chirp(ts,250,ts(end),50,"quadratic",0,"convex","complex");
Función spectrogram
Utilice la función spectrogram para calcular la STFT de la señal.
Divida la señal en segmentos, cada uno de muestras.
Especifique muestras de solapamiento entre segmentos contiguos.
Descarte el último segmento, el más corto.
Aplique una ventana de Bartlett a cada segmento.
Evalúe la transformada discreta de Fourier de cada segmento en puntos. De forma predeterminada,
spectrogramcalcula transformadas bilaterales en señales de valor complejo.
M = 49; L = 11; g = bartlett(M); Ndft = 1024; [s,f,t] = spectrogram(x,g,L,Ndft,fs);
Calcule y muestre el espectrograma, definido como la magnitud al cuadrado de la STFT, con la función waterplot.
waterplot(s,f,t)

Definición de STFT
Calcule la STFT de la señal de muestras con la definición. Divida la señal en segmentos superpuestos. Aplique una ventana a cada segmento y evalúe la transformada discreta de Fourier en puntos.
segs = framesig(1:length(x),M,OverlapLength=L); X = fft(x(segs).*g,Ndft);
Calcule los intervalos de tiempo y frecuencia de la STFT.
Para encontrar los valores de tiempo, divida el vector tiempo en segmentos superpuestos. Los valores de tiempo son los puntos medios de los segmentos, y cada segmento se trata como un intervalo abierto en el extremo inferior.
Para encontrar los valores de frecuencia, especifique un intervalo de Nyquist cerrado en la frecuencia cero y abierto en el extremo inferior.
framedT = ts(segs); tint = mean(framedT(2:end,:)); fint = 0:fs/Ndft:fs-fs/Ndft;
Compare la salida de spectrogram con la definición. Muestre el espectrograma.
maxdiff = max(max(abs(s-X)))
maxdiff = 0
waterplot(X,fint,tint)

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency (Hz)") ylabel("Time (s)") end
Genere una señal compuesta por un chirp muestreado a 1,4 kHz durante 2 segundos. La frecuencia del chirp disminuye linealmente de 600 Hz a 100 Hz durante el tiempo de medición.
fs = 1400; x = chirp(0:1/fs:2,600,2,100);
Valores predeterminados de stft
Calcule la STFT de la señal con las funciones spectrogram y stft. Utilice los valores predeterminados de la función stft:
Divida la señal en segmentos de 128 muestras y aplique una ventana periódica de Hann a cada segmento.
Especifique 96 muestras de solapamiento entre segmentos contiguos. Esta longitud equivale al 75% de la longitud de la ventana.
Especifique 128 puntos de la DFT y centre la STFT en la frecuencia cero, con la frecuencia expresada en hercios.
Compruebe que los dos resultados son iguales.
M = 128; g = hann(M,"periodic"); L = 0.75*M; Ndft = 128; [sp,fp,tp] = spectrogram(x,g,L,Ndft,fs,"centered"); [s,f,t] = stft(x,fs); dff = max(max(abs(sp-s)))
dff = 0
Represente las dos salidas con la función mesh.
nexttile mesh(tp,fp,abs(sp).^2) title("spectrogram") view(2), axis tight nexttile mesh(t,f,abs(s).^2) title("stft") view(2), axis tight

Valores predeterminados de spectrogram
Repita el cálculo utilizando los valores predeterminados de la función spectrogram:
Divida la señal en segmentos de longitud , donde es la longitud de la señal. Aplique una ventana de Hamming a cada segmento.
Especifique el 50% de solapamiento entre segmentos.
Para calcular la FFT, utilice puntos. Calcule el espectrograma solo para las frecuencias normalizadas positivas.
M = floor(length(x)/4.5); g = hamming(M); L = floor(M/2); Ndft = max(256,2^nextpow2(M)); [sx,fx,tx] = spectrogram(x); [st,ft,tt] = stft(x,Window=g,OverlapLength=L, ... FFTLength=Ndft,FrequencyRange="onesided"); dff = max(max(sx-st))
dff = 0
Represente las dos salidas con la función waterplot. Divida el eje de la frecuencia por en ambos casos. Para la salida de stft, divida los números de muestra por la tasa de muestreo efectiva, .
figure nexttile waterplot(sx,fx/pi,tx) title("spectrogram") nexttile waterplot(st,ft/pi,tt/(2*pi)) title("stft")

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency/\pi") ylabel("Samples") end
Utilice la función spectrogram para medir y realizar un seguimiento de la frecuencia instantánea de una señal.
Genere un chirp cuadrático muestreado a 1 kHz durante dos segundos. Especifique el chirp de forma que su frecuencia sea inicialmente 100 Hz y aumente a 200 Hz al pasar un segundo.
fs = 1000;
t = 0:1/fs:2-1/fs;
y = chirp(t,100,1,200,'quadratic');Calcule el espectro del chirp utilizando la transformada de Fourier de tiempo corto implementada en la función spectrogram. Divida la señal en secciones de longitud 100, dispuestas en ventanas con una ventana Hamming. Especifique 80 muestras de solapamiento entre secciones contiguas y evalúe el espectro en frecuencias .
spectrogram(y,100,80,100,fs,'yaxis')
Realice un seguimiento de la frecuencia del chirp buscando la cresta de tiempo-frecuencia con más energía en los puntos de tiempo . Superponga la frecuencia instantánea en la gráfica del espectrograma.
[~,f,t,p] = spectrogram(y,100,80,100,fs); [fridge,~,lr] = tfridge(p,f); hold on plot3(t,fridge,abs(p(lr)),'LineWidth',4) hold off

Genere 512 muestras de un chirp con contenido de frecuencia que varíe sinusoidalmente.
N = 512; n = 0:N-1; x = exp(1j*pi*sin(8*n/N)*32);
Calcule la transformada de Fourier de tiempo corto bilateral centrada del chirp. Divida la señal en segmentos de 32 muestras con un solapamiento de 16 muestras. Especifique 64 puntos DFT. Represente el espectrograma.
[scalar,fs,ts] = spectrogram(x,32,16,64,'centered'); spectrogram(x,32,16,64,'centered','yaxis')

Obtenga el mismo resultado calculando el espectrograma en 64 frecuencias equiespaciadas a lo largo del intervalo . La opción 'centered' no es necesaria.
fintv = -pi+pi/32:pi/32:pi;
[vector,fv,tv] = spectrogram(x,32,16,fintv);
spectrogram(x,32,16,fintv,'yaxis')
Genere una señal que conste de un oscilador controlado por tensión y tres átomos gaussianos. La señal se muestrea a kHz durante 2 segundos.
fs = 2000; tx = 0:1/fs:2; gaussFun = @(A,x,mu,f) exp(-(x-mu).^2/(2*0.03^2)).*sin(2*pi*f.*x)*A'; s = gaussFun([1 1 1],tx',[0.1 0.65 1],[2 6 2]*100)*1.5; x = vco(chirp(tx+.1,0,tx(end),3).*exp(-2*(tx-1).^2),[0.1 0.4]*fs,fs); x = s+x';
Transformadas de Fourier de tiempo corto
Utilice la función pspectrum para calcular la STFT.
Divida la señal de muestras en segmentos con longitud muestras, correspondientes a una resolución temporal de milisegundos.
Especifique muestras o el 20% de solapamiento entre los segmentos contiguos.
Añada una ventana de Kaiser a cada segmento y especifique un manchado de .
M = 80; L = 16; lk = 0.7; [S,F,T] = pspectrum(x,fs,"spectrogram", ... TimeResolution=M/fs,OverlapPercent=L/M*100, ... Leakage=lk);
Compárela con el resultado obtenido con la función spectrogram.
Especifique la longitud de la ventana y el solapamiento directamente en las muestras.
pspectrumsiempre usa una ventana de Kaiser como . El manchado y el factor de forma de la ventana están relacionados por .pspectrumsiempre usa puntos cuando calcula la transformada discreta de Fourier. Puede especificar este número si desea calcular la transformada en un rango de frecuencias bilateral o centrado. Sin embargo, en las transformadas unilaterales, que son las predeterminadas para las señales reales,spectrogramutiliza puntos. Como alternativa, puede especificar el vector de frecuencias en el que desea calcular la transformada, como en este ejemplo.Si una señal no puede dividirse exactamente en segmentos,
spectrogramla trunca, mientras quepspectrumla rellena con ceros para crear un segmento extra. Para que las salidas sean equivalentes, elimine el segmento final y el elemento final del vector de tiempo.spectrogramdevuelve la STFT, cuya magnitud elevada al cuadrado es el espectrograma.pspectrumdevuelve el espectro de potencia segmento a segmento, que ya está elevado al cuadrado pero se divide por un factor de antes de elevarlo al cuadrado.En las transformadas unilaterales,
pspectrumañade un factor extra de 2 al espectrograma.
g = kaiser(M,40*(1-lk)); k = (length(x)-L)/(M-L); if k~=floor(k) S = S(:,1:floor(k)); T = T(1:floor(k)); end [s,f,t] = spectrogram(x/sum(g)*sqrt(2),g,L,F,fs);
Para mostrar los espectrogramas calculados por las dos funciones, utilice la función waterplot.
subplot(2,1,1) waterplot(sqrt(S),F,T) title("pspectrum") subplot(2,1,2) waterplot(s,f,t) title("spectrogram")

maxd = max(max(abs(abs(s).^2-S)))
maxd = 2.4419e-08
Espectros de potencia y gráficas de conveniencia
La función spectrogram tiene un cuarto argumento que se corresponde con el espectro de potencia segmento a segmento o con la densidad espectral de potencia. Al igual que la salida de pspectrum, el argumento ps ya está elevado al cuadrado e incluye el factor de normalización . En los espectrogramas unilaterales de señales reales, hay que incluir el factor adicional de 2. Establezca el argumento de escala de la función en "power".
[~,~,~,ps] = spectrogram(x*sqrt(2),g,L,F,fs,"power");
max(abs(S(:)-ps(:)))ans = 2.4419e-08
Cuando se llaman sin argumentos de salida, tanto pspectrum como spectrogram representan el espectrograma de la señal en decibelios. Incluya el factor de 2 en los espectrogramas unilaterales. Establezca que los mapas de colores sean los mismos en ambas gráficas. Fije los límites del eje x en los mismos valores para hacer visible el segmento extra al final de la gráfica de pspectrum. En la gráfica de spectrogram, muestre la frecuencia en el eje y.
subplot(2,1,1) pspectrum(x,fs,"spectrogram", ... TimeResolution=M/fs,OverlapPercent=L/M*100, ... Leakage=lk) title("pspectrum") cc = clim; xl = xlim; subplot(2,1,2) spectrogram(x*sqrt(2),g,L,F,fs,"power","yaxis") title("spectrogram") clim(cc) xlim(xl)

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency (Hz)") ylabel("Time (s)") end
Genere una señal de chirp muestreada durante 2 segundos a 1 Hz. Especifique el chirp de forma que su frecuencia sea inicialmente 100 Hz y aumente a 200 Hz al pasar 1 segundo.
fs = 1000;
t = 0:1/fs:2;
y = chirp(t,100,1,200,"quadratic");Calcule el espectrograma reasignado de la señal.
Divida la señal en secciones de longitud 128, dispuestas en ventanas con una ventana de Kaiser con el parámetro de forma .
Especifique 120 muestras de solapamiento entre secciones contiguas.
Evalúe el espectro en frecuencias y bins de tiempo .
Utilice la función spectrogram sin argumentos de salida para representar el espectrograma reasignado. Muestre la frecuencia en el eje y y el tiempo en el eje x.
spectrogram(y,kaiser(128,18),120,128,fs, ... "reassigned","yaxis")

Vuelva a generar la gráfica usando la función imagesc. Especifique la dirección del eje y para que los valores de frecuencia aumenten de abajo hacia arriba. Añada eps al espectrograma reasignado para evitar posibles infinitos negativos al convertir a decibelios.
[~,fr,tr,pxx] = spectrogram(y,kaiser(128,18),120,128,fs, ... "reassigned"); imagesc(tr,fr,pow2db(pxx+eps)) axis xy xlabel("Time (s)") ylabel("Frequency (Hz)") colorbar

Genere una señal de chirp muestreada durante 2 segundos a 1 Hz. Especifique el chirp de forma que su frecuencia sea inicialmente 100 Hz y aumente a 200 Hz al pasar 1 segundo.
Fs = 1000;
t = 0:1/Fs:2;
y = chirp(t,100,1,200,'quadratic');Calcule la densidad espectral de potencia (PSD) dependiente del tiempo de la señal.
Divida la señal en secciones de longitud 128, dispuestas en ventanas con una ventana de Kaiser con el parámetro de forma .
Especifique 120 muestras de solapamiento entre secciones contiguas.
Evalúe el espectro en frecuencias y bins de tiempo .
Obtenga como salida la frecuencia y el tiempo del centro de gravedad de cada estimación de PSD. Establezca en cero los elementos de la PSD inferiores a dB.
[~,~,~,pxx,fc,tc] = spectrogram(y,kaiser(128,18),120,128,Fs, ... 'MinThreshold',-30);
Represente los elementos distintos de cero como funciones de las frecuencias y tiempos del centro de gravedad.
plot(tc(pxx>0),fc(pxx>0),'.')
Genere una señal compuesta por un chirp de valor real muestreado a 2 kHz durante 2 segundos.
fs = 2000;
tx = 0:1/fs:2;
x = vco(-chirp(tx,0,tx(end),2).*exp(-3*(tx-1).^2), ...
[0.1 0.4]*fs,fs).*hann(length(tx))';Espectrograma bilateral
Calcule y represente la STFT bilateral de la señal.
Divida la señal en segmentos, cada uno de muestras.
Especifique muestras de solapamiento entre segmentos contiguos.
Descarte el último segmento, el más corto.
Aplique una ventana flat-top a cada segmento.
Evalúe la transformada discreta de Fourier de cada segmento en puntos, teniendo en cuenta que es un número impar.
M = 73;
L = 24;
g = flattopwin(M);
Ndft = 895;
neven = ~mod(Ndft,2);
[stwo,f,t] = spectrogram(x,g,L,Ndft,fs,"twosided");Utilice la función spectrogram sin argumentos de salida para representar el espectrograma bilateral.
spectrogram(x,g,L,Ndft,fs,"twosided","power","yaxis")

Calcule el espectrograma bilateral con la definición. Divida la señal en segmentos de muestras con muestras de solapamiento entre segmentos contiguos. Aplique una ventana a cada segmento y calcule la transformada discreta de Fourier en puntos.
y = framesig(x,M,Window=g,OverlapLength=L); Xtwo = fft(y,Ndft);
Calcule los intervalos de tiempo y frecuencia.
Para encontrar los valores de tiempo, divida el vector tiempo en segmentos superpuestos. Los valores de tiempo son los puntos medios de los segmentos, y cada segmento se trata como un intervalo abierto en el extremo inferior.
Para encontrar los valores de frecuencia, especifique un intervalo de Nyquist cerrado en la frecuencia cero y abierto en el extremo superior.
framedT = framesig(tx,M,OverlapLength=L); ttwo = mean(framedT(2:end,:)); ftwo = 0:fs/Ndft:fs*(1-1/Ndft);
Compare las salidas del spectrogram con las definiciones. Visualice los espectrogramas con la función waterplot.
diffs = [max(max(abs(stwo-Xtwo)));
max(abs(f-ftwo'));
max(abs(t-ttwo))]diffs = 3×1
10-12 ×
0
0.2274
0.0002
figure nexttile waterplot(Xtwo,ftwo,ttwo) title("Two-Sided, Definition") nexttile waterplot(stwo,f,t) title("Two-Sided, spectrogram Function")

Espectrograma centrado
Calcule el espectrograma centrado de la señal.
Utilice los mismos valores de tiempo que utilizó en la STFT bilateral.
Desplace el componente de frecuencia cero de la STFT hacia el centro del espectro con la función
fftshift.En los valores impares de , el intervalo de frecuencia está abierto en ambos extremos. En los valores pares de , el intervalo de frecuencia está abierto en el extremo inferior y cerrado en el extremo superior.
Compare las salidas y muestre los espectrogramas.
tcen = ttwo; if ~neven Xcen = fftshift(Xtwo,1); fcen = -fs/2*(1-1/Ndft):fs/Ndft:fs/2; else Xcen = fftshift(circshift(Xtwo,-1),1); fcen = (-fs/2*(1-1/Ndft):fs/Ndft:fs/2)+fs/Ndft/2; end [scen,f,t] = spectrogram(x,g,L,Ndft,fs,"centered"); diffs = [max(max(abs(scen-Xcen))); max(abs(f-fcen')); max(abs(t-tcen))]
diffs = 3×1
10-12 ×
0
0.2274
0.0002
figure nexttile waterplot(Xcen,fcen,tcen) title("Centered, Definition") nexttile waterplot(scen,f,t) title("Centered, spectrogram Function")

Espectrograma unilateral
Calcule el espectrograma unilateral de la señal.
Utilice los mismos valores de tiempo que utilizó en la STFT bilateral.
En los valores impares de , la STFT unilateral consiste en las primeras filas de la STFT bilateral. En los valores pares de , la STFT unilateral consiste en las primeras filas de la STFT bilateral.
En los valores impares de , el intervalo de frecuencia se cierra en la frecuencia cero y se abre en la frecuencia de Nyquist. En los valores pares de , el intervalo de frecuencia se cierra en ambos extremos.
Compare las salidas y muestre los espectrogramas. En señales de valor real, el argumento "onesided" es opcional.
tone = ttwo; if ~neven Xone = Xtwo(1:(Ndft+1)/2,:); else Xone = Xtwo(1:Ndft/2+1,:); end fone = 0:fs/Ndft:fs/2; [sone,f,t] = spectrogram(x,g,L,Ndft,fs); diffs = [max(max(abs(sone-Xone))); max(abs(f-fone')); max(abs(t-tone))]
diffs = 3×1
10-12 ×
0
0.1137
0.0002
figure nexttile waterplot(Xone,fone,tone) title("One-Sided, Definition") nexttile waterplot(sone,f,t) title("One-Sided, spectrogram Function")

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency (Hz)") ylabel("Time (s)") end
La función spectrogram tiene como cuarto argumento de salida una matriz que contiene la densidad espectral de potencia (PSD) o el espectro de potencia de cada segmento. El espectro de potencia es igual a la PSD multiplicada por el ancho de banda de ruido equivalente (ENBW) de la ventana.
Genere una señal compuesta por un chirp logarítmico muestreado a 1 kHz durante 1 segundo. El chirp tiene una frecuencia inicial de 400 Hz que disminuye a 10 Hz al final de la medición.
fs = 1000;
tt = 0:1/fs:1-1/fs;
y = chirp(tt,400,tt(end),10,"logarithmic");PSD de segmentos y espectros de potencia con tasa de muestreo
Divida la señal en segmentos de 102 muestras y aplique una ventana de Hann a cada uno. Especifique 12 muestras de solapamiento entre segmentos contiguos y 1024 puntos de la DFT.
M = 102; g = hann(M); L = 12; Ndft = 1024;
Calcule el espectrograma de la señal con el tipo de espectro de la PSD predeterminado. Genere la STFT y el arreglo de densidades espectrales de potencia de los segmentos.
[s,f,t,p] = spectrogram(y,g,L,Ndft,fs);
Repita el cálculo con el tipo de espectro especificado como "power". Obtenga como salida la STFT y el arreglo de espectros de potencia de los segmentos.
[r,~,~,q] = spectrogram(y,g,L,Ndft,fs,"power");Compruebe que el espectrograma es el mismo en ambos casos. Represente el espectrograma con una escala logarítmica para la frecuencia.
max(max(abs(s).^2-abs(r).^2))
ans = 0
waterfall(f,t,abs(s)'.^2) set(gca,XScale="log",... XDir="reverse",View=[30 50])

Compruebe que los espectros de potencia son iguales a las densidades espectrales de potencia multiplicadas por el ENBW de la ventana.
max(max(abs(q-p*enbw(g,fs))))
ans = 1.1102e-16
Compruebe que la matriz de espectros de potencia del segmento es proporcional al espectrograma. El factor de proporcionalidad es el cuadrado de la suma de los elementos de la ventana.
max(max(abs(s).^2-q*sum(g)^2))
ans = 0
PSD de segmentos y espectros de potencia con frecuencias normalizadas
Repita el cálculo, pero ahora trabaje en frecuencias normalizadas. Los resultados son los mismos cuando se especifica la tasa de muestreo como .
[~,~,~,pn] = spectrogram(y,g,L,Ndft);
[~,~,~,qn] = spectrogram(y,g,L,Ndft,"power");
max(max(abs(qn-pn*enbw(g,2*pi))))ans = 1.1102e-16
Cargue una señal de audio que contenga dos chirps decrecientes y un sonido de salpicadura de banda ancha. Calcule la transformada de Fourier de tiempo corto. Divida la forma de onda en segmentos de 400 muestras con 300 muestras de solapamiento. Represente el espectrograma.
load splat % To hear, type soundsc(y,Fs) sg = 400; ov = 300; spectrogram(y,sg,ov,[],Fs,"yaxis") colormap bone

Utilice la función spectrogram para emitir la densidad espectral de potencia (PSD) de la señal.
[s,f,t,p] = spectrogram(y,sg,ov,[],Fs);
Realice un seguimiento de los dos chirps utilizando la función medfreq. Para encontrar el chirp de baja frecuencia más potente, restrinja la búsqueda a las frecuencias por encima de 100 Hz y a los tiempos anteriores al inicio del sonido de banda ancha.
f1 = f > 100; t1 = t < 0.75; m1 = medfreq(p(f1,t1),f(f1));
Para encontrar el chirp de baja frecuencia más débil, restrinja la búsqueda a las frecuencias por encima de 2500 Hz y a tiempos entre 0,3 segundos y 0,65 segundos.
f2 = f > 2500; t2 = t > 0.3 & t < 0.65; m2 = medfreq(p(f2,t2),f(f2));
Superponga el resultado en el espectrograma. Divida los valores de frecuencia entre 1000 para expresarlos en kHz.
hold on plot(t(t1),m1/1000,LineWidth=4) plot(t(t2),m2/1000,LineWidth=4) hold off

Genere dos segundos de una señal muestreada a 10 kHz. Especifique la frecuencia instantánea de la señal como una función triangular de tiempo.
fs = 10e3; t = 0:1/fs:2; x1 = vco(sawtooth(2*pi*t,0.5),[0.1 0.4]*fs,fs);
Calcule y represente el espectrograma de la señal. Utilice una ventana de Kaiser de longitud 256 y parámetro de forma . Especifique 220 muestras de solapamiento sección a sección y 512 puntos DFT. Represente la frecuencia en el eje y. Utilice el mapa de colores y la vista predeterminados.
spectrogram(x1,kaiser(256,5),220,512,fs,'yaxis')
Cambie la vista para mostrar el espectrograma como gráfica de cascada. Establezca el mapa de colores en bone.
view(-45,65)
colormap bone
Desde R2025a
Represente los espectrogramas de cuatro señales en los identificadores de los ejes y los contenedores de los paneles. Cuando utiliza spectrogram sin argumentos de salida, la función devuelve una gráfica de conveniencia con la estimación de la densidad espectral de potencia (PSD). Para reproducir esta gráfica en un identificador de eje o un contenedor de panel específico, especifique spectrogram con un argumento de entrada Parent objetivo.
Cree cuatro señales oscilantes con una tasa de muestreo de 10 kHz durante tres segundos.
x1: Señal oscilante en forma de diente de sierrax2: Señal oscilante con disminución exponencialx3: Envolvente sinusoidal complejax4: Chirp de barrido cuadrático
Fs = 10e3; t = 0:1/Fs:3; x1 = vco(sawtooth(2*pi*t,0.5),[0.1 0.4]*Fs,Fs); x2 = vco(sin(2*pi*t).*exp(-t),[0.1 0.4]*Fs,Fs) ... + 0.01*sin(2*pi*0.25*Fs*t); x3 = exp(1j*pi*sin(4*t)*Fs/10); x4 = chirp(t,Fs/10,t(end),Fs/2.5,"quadratic");
Defina las especificaciones para calcular los espectrogramas de la señal: 512 puntos DFT, una ventana de Kaiser de 256 muestras y una longitud de solapamiento de 220 muestras.
nfft = 512; g = kaiser(256,5); ol = 220;
Representar espectrogramas en un identificador de ejes
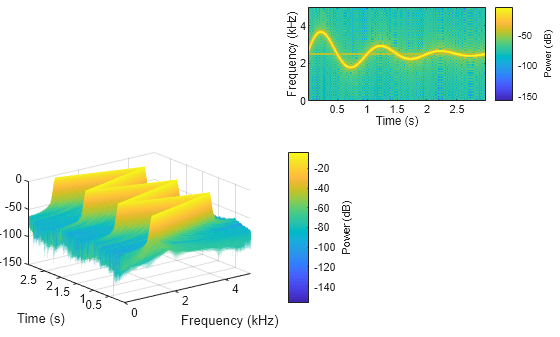
Cree dos identificadores de ejes en las esquinas suroeste y noreste de una nueva ventana de figura.
fig = figure; ax1 = axes(fig,Position=[0.05 0.1 0.55 0.45]); ax2 = axes(fig,Position=[0.55 0.7 0.42 0.28]);
Represente los espectros de potencia de las señales x1 y x2 en los ejes suroeste y noreste de la figura, respectivamente. Visualice el espectrograma de x1 en la línea de visión 3D predeterminada. Muestre las frecuencias en el eje y para el espectrograma de x2.
spectrogram(x1,g,ol,nfft,Fs,"power",Parent=ax1); view(ax1,3); spectrogram(x2,g,ol,nfft,Fs,"power","yaxis",Parent=ax2);
Representar espectrogramas en un identificador de ejes basado en la interfaz de usuario
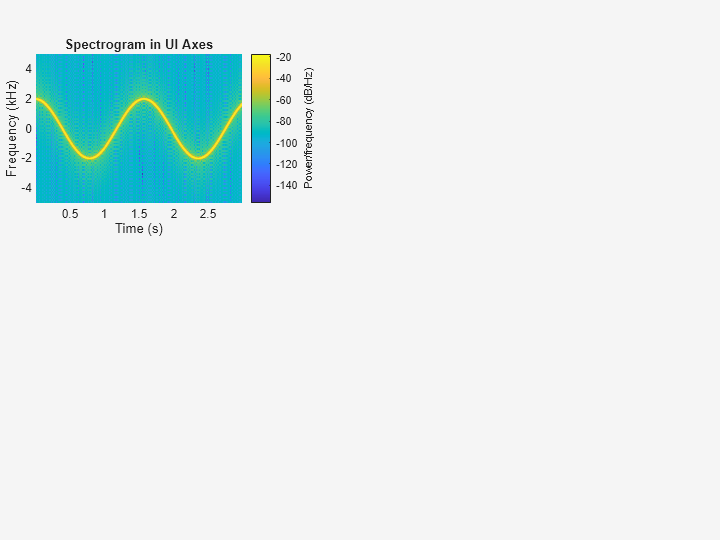
Cree un identificador de ejes en la esquina noroeste de una nueva ventana de figura de interfaz de usuario.
uif = uifigure(Position=[100 100 720 540]);
ax3 = uiaxes(uif,'Position',[5 305 300 200]);Represente la estimación de la PSD de la señal x3 en los ejes de la figura. Muestre las frecuencias en el eje y centradas en 0 kHz.
spectrogram(x3,g,ol,nfft,Fs,"centered","yaxis",Parent=ax3); title(ax3,"Spectrogram in UI Axes")
Representar espectrogramas en un contenedor de paneles
Añada un contenedor de paneles en la esquina sureste de la ventana de la figura de interfaz de usuario.
ax4 = uipanel(uif,Position=[300 5 400 325], ... Title="Spectrogram in UI Panel", ... BackgroundColor="white");
Represente la estimación de la PSD de la señal x4 en el contenedor de paneles. Muestre las frecuencias en el eje y.
spectrogram(x4,g,ol,nfft,Fs,"yaxis",Parent=ax4);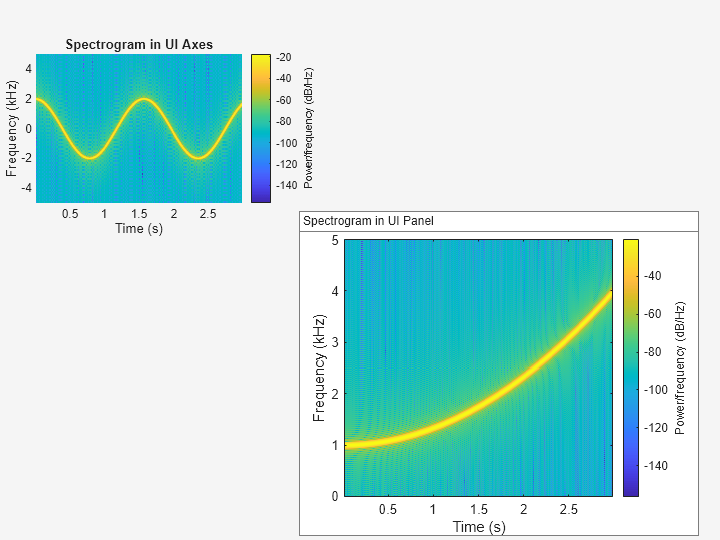
Argumentos de entrada
Señal de entrada, especificada como un vector fila o vector columna.
Ejemplo: cos(pi/4*(0:159))+randn(1,160) especifica una sinusoide integrada en ruido blanco gaussiano.
Tipos de datos: single | double
Soporte de números complejos: Sí
Ventana, especificada como un entero positivo o como un vector fila o vector columna. Utilice window para dividir la señal en segmentos:
Si
windowes un entero,spectrogramdividexen segmentos de longitudwindowy dispone en ventanas cada segmento con una ventana Hamming de esa longitud.Si
windowes un vector,spectrogramdividexen segmentos de la misma longitud que el vector y dispone en ventanas cada segmento utilizandowindow.
Si la longitud de x no puede dividirse exactamente en un número entero de segmentos con muestras solapadas noverlap, x se trunca en consecuencia.
Si especifica window como vacío, spectrogram utiliza una ventana Hamming de forma que x se divide en ocho segmentos con muestras solapadas noverlap.
Para obtener una lista de las ventanas disponibles, consulte Ventanas.
Ejemplo: hann(N+1) y (1-cos(2*pi*(0:N)'/N))/2 especifican ambas una ventana de Hann de longitud N + 1.
Número de muestras solapadas, especificado como entero no negativo.
Si
windowes escalar,noverlapdebe ser menor quewindow.Si
windowes un vector,noverlapdebe ser menos que la longitud dewindow.
Si especifica noverlap como vacío, spectrogram utiliza un número que genera un 50% de solapamiento entre segmentos. Si no se especifica la longitud del segmento, la función establece noverlap en ⌊Nx/4.5⌋, donde Nx es la longitud de la señal de entrada y los símbolos ⌊⌋ determinan la función de suelo.
Número de puntos DFT, especificado como escalar entero positivo. Si especifica nfft como vacío, spectrogram establece el parámetro en max(256,2p), donde p = ⌈log2 Nw⌉, los símbolos ⌈⌉ determinan la función de techo, y
Nw =
windowsiwindowes un escalar.Nw =
length(siwindow)windowes un vector.
Frecuencias normalizadas, especificadas como vector. w debe tener al menos dos elementos porque, de lo contrario, la función lo interpreta como nfft. Las frecuencias normalizadas están en rad/muestra.
Ejemplo: pi./[2 4]
Tipos de datos: single | double
Tasa de muestreo, especificada como un escalar positivo. La tasa de muestreo es el número de muestras por unidad de tiempo. Si la unidad de tiempo es el segundo, la tasa de muestreo estará en Hz.
Rango de frecuencia para la estimación de la PSD, especificado como "onesided", "twosided" o "centered". En señales de valor real, el valor predeterminado es "onesided". En señales de valor complejo, el valor predeterminado es "twosided", y especificar "onesided" da como resultado un error.
"onesided"devuelve el espectrograma unilateral de una señal de entrada real. Sinfftes par,pstienenfft/2 + 1 filas y se calcula en el intervalo [0, π] rad/muestra. Sinfftes impar,pstiene (nfft+ 1)/2 filas y el intervalo es [0, π) rad/muestra. Si especificafs, los intervalos son respectivamente [0,fs/2] ciclos/unidad de tiempo y [0,fs/2) ciclos/unidad de tiempo."twosided"devuelve el espectrograma bilateral de una señal de valor real o complejo.pstienenfftfilas y se calcula en el intervalo [0, 2π) rad/muestra. Si especificafs, el intervalo es [0,fs] ciclos/unidad de tiempo."centered"devuelve el espectrograma bilateral centrado de una señal de valor real o complejo.pstienenfftfilas. Sinfftes par,psse calcula en el intervalo (–π, π] rad/muestra. Sinfftes impar,psse calcula en (–π, π) rad/muestra. Si especificafs, los intervalos son respectivamente (–fs/2,fs/2] ciclos/unidad de tiempo y (–fs/2,fs/2) ciclos/unidad de tiempo.
Tipos de datos: char | string
Escalado del espectro de potencia, especificado como "psd" o "power".
Omitir
spectrumtypeo especificar"psd"devuelve la densidad espectral de potencia.Especificando
"power", se escala cada estimación de PSD por el ancho de banda de ruido equivalente de la ventana. El resultado es una estimación de la potencia en cada frecuencia. Si la opción"reassigned"está activada, la función integra la PSD en la anchura de cada bin de frecuencia antes de reasignar.
Tipos de datos: char | string
Eje de visualización de la frecuencia, especificado como "xaxis" o "yaxis".
"xaxis"muestra la frecuencia en el eje x y el tiempo en el eje y."yaxis"muestra la frecuencia en el eje y y el tiempo en el eje x.
Este argumento se ignora si se llama a spectrogram con argumentos de salida.
Tipos de datos: char | string
Argumentos de par nombre-valor
Especifique pares de argumentos opcionales como Name1=Value1,...,NameN=ValueN, donde Name es el nombre del argumento y Value es el valor correspondiente. Los argumentos de nombre-valor deben aparecer después de otros argumentos. Sin embargo, el orden de los pares no importa.
Ejemplo: spectrogram(x,100,OutputTimeDimension="downrows") divide x en segmentos de longitud 100 y dispone en ventanas cada segmento con una ventana Hamming de esa longitud. La salida del espectrograma tiene una dimensión de tiempo en las filas.
En las versiones anteriores a la R2021a, utilice comas para separar cada nombre y valor, y encierre Name entre comillas.
Ejemplo: spectrogram(x,100,'OutputTimeDimension','downrows') divide x en segmentos de longitud 100 y dispone en ventanas cada segmento con una ventana Hamming de esa longitud. La salida del espectrograma tiene una dimensión de tiempo en las filas.
Umbral, especificado como un escalar real expresado en decibelios. spectrogram establece en cero esos elementos de s de forma que 10 log10(s) ≤ thresh.
Dimensión de tiempo de salida, especificada como "acrosscolumns" o "downrows". Establezca este valor en "downrows" si desea la dimensión de tiempo de s, ps, fc y tc en las filas y la dimensión de frecuencia en las columnas. Establezca este valor en "acrosscolumns" si desea la dimensión de tiempo de s, ps, fc y tc en las columnas y la dimensión de frecuencia en las filas. Esta entrada se ignora si se llama a la función sin argumentos de salida.
Tipos de datos: char | string
Desde R2025a
Objeto principal objetivo, especificado como un objeto Axes, un objeto UIAxes o un objeto Panel.
Si especifica
Parent, la funciónspectrogramrepresenta la PSD o el espectro de potencia como una gráfica de superficie en el objeto principal objetivo especificado. La función devuelve la gráfica incluso si la llama con o sin argumentos de salida.Si no se especifica
Parenty no se especifican argumentos de salida, la funciónspectrogramrepresenta la PSD o el espectro de potencia como una gráfica de superficie en los ejes o el gráfico actuales que devuelvegca.
Para obtener más información sobre objetivos, consulte Objetos de gráficas. Para obtener más información sobre la relación principal-secundario en gráficas de MATLAB®, consulte Jerarquía de objetos de gráficas.
Tipos de datos: Axes | UIAxes | Panel
Argumentos de salida
Transformada de Fourier de tiempo corto, devuelta como matriz. El tiempo aumenta en las columnas de s y la frecuencia se reduce en las filas, empezando desde cero.
Nota
Cuando freqrange se establece en "onesided", spectrogram emite los valores s en el rango positivo de Nyquist y no conserva la potencia total.
s no se ve afectada por la opción "reassigned".
Instantes de tiempo, devueltos como vector. Los valores de tiempo en t corresponden al punto de en medio de cada segmento.
Densidad espectral de potencia (PSD) o espectro de potencia, devueltos como matriz.
Si
xes real yfreqrangese deja sin especificar o se establece en"onesided",pscontiene la estimación del periodograma unilateral modificada de la PSD o del espectro de potencia de cada segmento. La función multiplica la potencia por 2 en todas las frecuencias excepto 0 y la frecuencia de Nyquist para conservar la potencia total.Si
xes de valor complejo o sifreqrangese establece en"twosided"o"centered",pscontiene la estimación del periodograma bilateral modificada de la PSD o del espectro de potencia de cada segmento.Si se especifica un vector de frecuencias normalizadas en
wo un vector de frecuencias cíclicas enf,pscontiene la estimación del periodograma modificada de la PSD o espectro de potencia de cada segmento evaluado en las frecuencias de entrada.
Frecuencias y tiempos del centro de energía, devueltos como matrices del mismo tamaño que la transformada de Fourier de tiempo corto. Si no especifica una tasa de muestreo, los elementos de fc se devuelven como frecuencias normalizadas.
Más acerca de
La transformada de Fourier de tiempo corto (STFT) se utiliza para analizar cómo cambia el contenido de frecuencia de una señal no estacionaria a lo largo del tiempo. La magnitud al cuadrado de la STFT se conoce como la representación de tiempo-frecuencia del espectrograma de la señal. Para obtener más información sobre el espectrograma y cómo calcularlo mediante las funciones de Signal Processing Toolbox™, consulte Cálculo de espectrogramas con Signal Processing Toolbox.
La STFT de una señal se calcula deslizando una ventana de análisis g(n) de longitud M sobre la señal y calculando la transformada discreta de Fourier (DFT) de cada segmento de los datos con ventana. La ventana salta sobre la señal original en intervalos de R muestras, lo que equivale a L = M – R muestras de solapamiento entre segmentos contiguos. La mayoría de las funciones de ventana se estrechan en los bordes para evitar el anillamiento espectral. La DFT de cada segmento con ventana se añade a una matriz de valor complejo que contiene la magnitud y la fase de cada punto en tiempo y frecuencia. La matriz STFT tiene
columnas, donde Nx es la longitud de la señal x(n) y los símbolos ⌊⌋ denotan la función de suelo. En las transformadas centradas y bilaterales, el número de filas de la matriz es igual a NDFT, el número de puntos de la DFT, y en las transformadas unilaterales de señales de valor real es un número impar cercano a NDFT/2.
La columna m de la matriz de la STFT contiene la DFT de los datos con ventana centrados en el tiempo mR:
Sugerencias
Si una transformada de Fourier de tiempo corto tiene ceros, su conversión a decibelios da como resultado infinitos negativos que no pueden representarse. Para evitar esta posible dificultad, spectrogram añade eps a la transformada de Fourier de tiempo corto cuando la llama sin argumentos de salida.
Referencias
[1] Boashash, Boualem, ed. Time Frequency Signal Analysis and Processing: A Comprehensive Reference. Second edition. EURASIP and Academic Press Series in Signal and Image Processing. Amsterdam and Boston: Academic Press, 2016.
[2] Chassande-Motin, Éric, François Auger, and Patrick Flandrin. "Reassignment." In Time-Frequency Analysis: Concepts and Methods. Edited by Franz Hlawatsch and François Auger. London: ISTE/John Wiley and Sons, 2008.
[3] Fulop, Sean A., and Kelly Fitz. "Algorithms for computing the time-corrected instantaneous frequency (reassigned) spectrogram, with applications." Journal of the Acoustical Society of America. Vol. 119, January 2006, pp. 360–371.
[4] Oppenheim, Alan V., and Ronald W. Schafer, with John R. Buck. Discrete-Time Signal Processing. Second edition. Upper Saddle River, NJ: Prentice Hall, 1999.
[5] Rabiner, Lawrence R., and Ronald W. Schafer. Digital Processing of Speech Signals. Englewood Cliffs, NJ: Prentice-Hall, 1978.
Capacidades ampliadas
La función spectrogram es compatible con arreglos altos con las siguientes notas y limitaciones de uso:
La entrada debe ser un vector columna alto.
El argumento
windowdebe especificarse siempre.OutputTimeDimensiondebe especificarse siempre y establecerse en"downrows".La opción
reassignedno es compatible.Las sintaxis sin argumentos de salida no son compatibles.
Para obtener más información, consulte Arreglos altos.
Notas y limitaciones de uso:
El argumento de entrada
Parentno es compatible.Los argumentos especificados utilizando argumentos nombre-valor deben ser constantes en tiempo de compilación.
Notas y limitaciones de uso:
Los argumentos especificados utilizando argumentos nombre-valor deben ser constantes en tiempo de compilación.
windowde tamaño variable debe ser de doble precisión.
Notas y limitaciones de uso:
La sintaxis sin argumentos de salida no es compatible.
El vector de frecuencia debe estar espaciado uniformemente.
Para obtener más información, consulte Ejecutar funciones de MATLAB en entornos basados en subprocesos.
Esta función es totalmente compatible con los arreglos de GPU. Para obtener más información, consulte Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Historial de versiones
Introducido antes de R2006aLa función spectrogram admite las entradas de ventana de tamaño variable y precisión simple para la generación de código.
La función spectrogram admite las entradas de precisión simple y la generación de código para unidades de procesamiento gráfico (GPU). Debe tener MATLAB Coder™ y GPU Coder™ para generar el código de CUDA®.
Ahora puede usar la tarea de Live Editor Create Plot para visualizar la salida de spectrogram de forma interactiva. Puede seleccionar diferentes tipos de gráficas y establecer parámetros opcionales. La tarea también genera automáticamente código que se convierte en parte de su script en vivo.
Consulte también
Apps
Funciones
goertzel|istft|periodogram|pspectrum|pwelch|stft|xspectrogram
Temas
Sitios web externos
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)