resume
Resume training of Gaussian kernel classification model
Syntax
Description
UpdatedMdl = resume(Mdl,X,Y)Mdl,
including the training data (predictor data in X and class
labels in Y) and the feature expansion. The training starts
at the current estimated parameters in Mdl. The function
returns a new binary Gaussian kernel classification model
UpdatedMdl.
UpdatedMdl = resume(Mdl,Tbl,ResponseVarName)Tbl and the
true class labels in Tbl.ResponseVarName.
UpdatedMdl = resume(Mdl,Tbl,Y)Tbl and
the true class labels in Y.
UpdatedMdl = resume(___,Name,Value)
[
also returns the fit information in the structure array
UpdatedMdl,FitInfo] = resume(___)FitInfo.
Examples
Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, either bad ('b') or good ('g').
load ionospherePartition the data set into training and test sets. Specify a 20% holdout sample for the test set.
rng('default') % For reproducibility Partition = cvpartition(Y,'Holdout',0.20); trainingInds = training(Partition); % Indices for the training set XTrain = X(trainingInds,:); YTrain = Y(trainingInds); testInds = test(Partition); % Indices for the test set XTest = X(testInds,:); YTest = Y(testInds);
Train a binary kernel classification model that identifies whether the radar return is bad ('b') or good ('g').
Mdl = fitckernel(XTrain,YTrain,'IterationLimit',5,'Verbose',1);
|=================================================================================================================| | Solver | Pass | Iteration | Objective | Step | Gradient | Relative | sum(beta~=0) | | | | | | | magnitude | change in Beta | | |=================================================================================================================| | LBFGS | 1 | 0 | 1.000000e+00 | 0.000000e+00 | 2.811388e-01 | | 0 | | LBFGS | 1 | 1 | 7.585395e-01 | 4.000000e+00 | 3.594306e-01 | 1.000000e+00 | 2048 | | LBFGS | 1 | 2 | 7.160994e-01 | 1.000000e+00 | 2.028470e-01 | 6.923988e-01 | 2048 | | LBFGS | 1 | 3 | 6.825272e-01 | 1.000000e+00 | 2.846975e-02 | 2.388909e-01 | 2048 | | LBFGS | 1 | 4 | 6.699435e-01 | 1.000000e+00 | 1.779359e-02 | 1.325304e-01 | 2048 | | LBFGS | 1 | 5 | 6.535619e-01 | 1.000000e+00 | 2.669039e-01 | 4.112952e-01 | 2048 | |=================================================================================================================|
Mdl is a ClassificationKernel model.
Predict the test-set labels, construct a confusion matrix for the test set, and estimate the classification error for the test set.
label = predict(Mdl,XTest); ConfusionTest = confusionchart(YTest,label);

L = loss(Mdl,XTest,YTest)
L = 0.3594
Mdl misclassifies all bad radar returns as good returns.
Continue training by using resume. This function continues training with the same options used for training Mdl.
UpdatedMdl = resume(Mdl,XTrain,YTrain);
|=================================================================================================================| | Solver | Pass | Iteration | Objective | Step | Gradient | Relative | sum(beta~=0) | | | | | | | magnitude | change in Beta | | |=================================================================================================================| | LBFGS | 1 | 0 | 6.535619e-01 | 0.000000e+00 | 2.669039e-01 | | 2048 | | LBFGS | 1 | 1 | 6.132547e-01 | 1.000000e+00 | 6.355537e-03 | 1.522092e-01 | 2048 | | LBFGS | 1 | 2 | 5.938316e-01 | 4.000000e+00 | 3.202847e-02 | 1.498036e-01 | 2048 | | LBFGS | 1 | 3 | 4.169274e-01 | 1.000000e+00 | 1.530249e-01 | 7.234253e-01 | 2048 | | LBFGS | 1 | 4 | 3.679212e-01 | 5.000000e-01 | 2.740214e-01 | 2.495886e-01 | 2048 | | LBFGS | 1 | 5 | 3.332261e-01 | 1.000000e+00 | 1.423488e-02 | 9.558680e-02 | 2048 | | LBFGS | 1 | 6 | 3.235335e-01 | 1.000000e+00 | 7.117438e-03 | 7.137260e-02 | 2048 | | LBFGS | 1 | 7 | 3.112331e-01 | 1.000000e+00 | 6.049822e-02 | 1.252157e-01 | 2048 | | LBFGS | 1 | 8 | 2.972144e-01 | 1.000000e+00 | 7.117438e-03 | 5.796240e-02 | 2048 | | LBFGS | 1 | 9 | 2.837450e-01 | 1.000000e+00 | 8.185053e-02 | 1.484733e-01 | 2048 | | LBFGS | 1 | 10 | 2.797642e-01 | 1.000000e+00 | 3.558719e-02 | 5.856842e-02 | 2048 | | LBFGS | 1 | 11 | 2.771280e-01 | 1.000000e+00 | 2.846975e-02 | 2.349433e-02 | 2048 | | LBFGS | 1 | 12 | 2.741570e-01 | 1.000000e+00 | 3.914591e-02 | 3.113194e-02 | 2048 | | LBFGS | 1 | 13 | 2.725701e-01 | 5.000000e-01 | 1.067616e-01 | 8.729821e-02 | 2048 | | LBFGS | 1 | 14 | 2.667147e-01 | 1.000000e+00 | 3.914591e-02 | 3.491723e-02 | 2048 | | LBFGS | 1 | 15 | 2.621152e-01 | 1.000000e+00 | 7.117438e-03 | 5.104726e-02 | 2048 | | LBFGS | 1 | 16 | 2.601652e-01 | 1.000000e+00 | 3.558719e-02 | 3.764904e-02 | 2048 | | LBFGS | 1 | 17 | 2.589052e-01 | 1.000000e+00 | 3.202847e-02 | 3.655744e-02 | 2048 | | LBFGS | 1 | 18 | 2.583185e-01 | 1.000000e+00 | 7.117438e-03 | 6.490571e-02 | 2048 | | LBFGS | 1 | 19 | 2.556482e-01 | 1.000000e+00 | 9.252669e-02 | 4.601390e-02 | 2048 | | LBFGS | 1 | 20 | 2.542643e-01 | 1.000000e+00 | 7.117438e-02 | 4.141838e-02 | 2048 | |=================================================================================================================| | Solver | Pass | Iteration | Objective | Step | Gradient | Relative | sum(beta~=0) | | | | | | | magnitude | change in Beta | | |=================================================================================================================| | LBFGS | 1 | 21 | 2.532117e-01 | 1.000000e+00 | 1.067616e-02 | 1.661720e-02 | 2048 | | LBFGS | 1 | 22 | 2.529890e-01 | 1.000000e+00 | 2.135231e-02 | 1.231678e-02 | 2048 | | LBFGS | 1 | 23 | 2.523232e-01 | 1.000000e+00 | 3.202847e-02 | 1.958586e-02 | 2048 | | LBFGS | 1 | 24 | 2.506736e-01 | 1.000000e+00 | 1.779359e-02 | 2.474613e-02 | 2048 | | LBFGS | 1 | 25 | 2.501995e-01 | 1.000000e+00 | 1.779359e-02 | 2.514352e-02 | 2048 | | LBFGS | 1 | 26 | 2.488242e-01 | 1.000000e+00 | 3.558719e-03 | 1.531810e-02 | 2048 | | LBFGS | 1 | 27 | 2.485295e-01 | 5.000000e-01 | 3.202847e-02 | 1.229760e-02 | 2048 | | LBFGS | 1 | 28 | 2.482244e-01 | 1.000000e+00 | 4.270463e-02 | 8.970983e-03 | 2048 | | LBFGS | 1 | 29 | 2.479714e-01 | 1.000000e+00 | 3.558719e-03 | 7.393900e-03 | 2048 | | LBFGS | 1 | 30 | 2.477316e-01 | 1.000000e+00 | 3.202847e-02 | 3.268087e-03 | 2048 | | LBFGS | 1 | 31 | 2.476178e-01 | 2.500000e-01 | 3.202847e-02 | 5.445890e-03 | 2048 | | LBFGS | 1 | 32 | 2.474874e-01 | 1.000000e+00 | 1.779359e-02 | 3.535903e-03 | 2048 | | LBFGS | 1 | 33 | 2.473980e-01 | 1.000000e+00 | 7.117438e-03 | 2.821725e-03 | 2048 | | LBFGS | 1 | 34 | 2.472935e-01 | 1.000000e+00 | 3.558719e-03 | 2.699880e-03 | 2048 | | LBFGS | 1 | 35 | 2.471418e-01 | 1.000000e+00 | 3.558719e-03 | 1.242523e-02 | 2048 | | LBFGS | 1 | 36 | 2.469862e-01 | 1.000000e+00 | 2.846975e-02 | 7.895605e-03 | 2048 | | LBFGS | 1 | 37 | 2.469598e-01 | 1.000000e+00 | 2.135231e-02 | 6.657676e-03 | 2048 | | LBFGS | 1 | 38 | 2.466941e-01 | 1.000000e+00 | 3.558719e-02 | 4.654690e-03 | 2048 | | LBFGS | 1 | 39 | 2.466660e-01 | 5.000000e-01 | 1.423488e-02 | 2.885769e-03 | 2048 | | LBFGS | 1 | 40 | 2.465605e-01 | 1.000000e+00 | 3.558719e-03 | 4.562565e-03 | 2048 | |=================================================================================================================| | Solver | Pass | Iteration | Objective | Step | Gradient | Relative | sum(beta~=0) | | | | | | | magnitude | change in Beta | | |=================================================================================================================| | LBFGS | 1 | 41 | 2.465362e-01 | 1.000000e+00 | 1.423488e-02 | 5.652180e-03 | 2048 | | LBFGS | 1 | 42 | 2.463528e-01 | 1.000000e+00 | 3.558719e-03 | 2.389759e-03 | 2048 | | LBFGS | 1 | 43 | 2.463207e-01 | 1.000000e+00 | 1.511170e-03 | 3.738286e-03 | 2048 | | LBFGS | 1 | 44 | 2.462585e-01 | 5.000000e-01 | 7.117438e-02 | 2.321693e-03 | 2048 | | LBFGS | 1 | 45 | 2.461742e-01 | 1.000000e+00 | 7.117438e-03 | 2.599725e-03 | 2048 | | LBFGS | 1 | 46 | 2.461434e-01 | 1.000000e+00 | 3.202847e-02 | 3.186923e-03 | 2048 | | LBFGS | 1 | 47 | 2.461115e-01 | 1.000000e+00 | 7.117438e-03 | 1.530711e-03 | 2048 | | LBFGS | 1 | 48 | 2.460814e-01 | 1.000000e+00 | 1.067616e-02 | 1.811714e-03 | 2048 | | LBFGS | 1 | 49 | 2.460533e-01 | 5.000000e-01 | 1.423488e-02 | 1.012252e-03 | 2048 | | LBFGS | 1 | 50 | 2.460111e-01 | 1.000000e+00 | 1.423488e-02 | 4.166762e-03 | 2048 | | LBFGS | 1 | 51 | 2.459414e-01 | 1.000000e+00 | 1.067616e-02 | 3.271946e-03 | 2048 | | LBFGS | 1 | 52 | 2.458809e-01 | 1.000000e+00 | 1.423488e-02 | 1.846440e-03 | 2048 | | LBFGS | 1 | 53 | 2.458479e-01 | 1.000000e+00 | 1.067616e-02 | 1.180871e-03 | 2048 | | LBFGS | 1 | 54 | 2.458146e-01 | 1.000000e+00 | 1.455008e-03 | 1.422954e-03 | 2048 | | LBFGS | 1 | 55 | 2.457878e-01 | 1.000000e+00 | 7.117438e-03 | 1.880892e-03 | 2048 | | LBFGS | 1 | 56 | 2.457519e-01 | 1.000000e+00 | 2.491103e-02 | 1.074764e-03 | 2048 | | LBFGS | 1 | 57 | 2.457420e-01 | 1.000000e+00 | 7.473310e-02 | 9.511878e-04 | 2048 | | LBFGS | 1 | 58 | 2.457212e-01 | 1.000000e+00 | 3.558719e-03 | 3.718564e-04 | 2048 | | LBFGS | 1 | 59 | 2.457089e-01 | 1.000000e+00 | 4.270463e-02 | 6.237270e-04 | 2048 | | LBFGS | 1 | 60 | 2.457047e-01 | 5.000000e-01 | 1.423488e-02 | 3.647573e-04 | 2048 | |=================================================================================================================| | Solver | Pass | Iteration | Objective | Step | Gradient | Relative | sum(beta~=0) | | | | | | | magnitude | change in Beta | | |=================================================================================================================| | LBFGS | 1 | 61 | 2.456991e-01 | 1.000000e+00 | 1.423488e-02 | 5.666884e-04 | 2048 | | LBFGS | 1 | 62 | 2.456898e-01 | 1.000000e+00 | 1.779359e-02 | 4.697056e-04 | 2048 | | LBFGS | 1 | 63 | 2.456792e-01 | 1.000000e+00 | 1.779359e-02 | 5.984927e-04 | 2048 | | LBFGS | 1 | 64 | 2.456603e-01 | 1.000000e+00 | 1.403782e-03 | 5.414985e-04 | 2048 | | LBFGS | 1 | 65 | 2.456482e-01 | 1.000000e+00 | 3.558719e-03 | 6.506293e-04 | 2048 | | LBFGS | 1 | 66 | 2.456358e-01 | 1.000000e+00 | 1.476262e-03 | 1.284139e-03 | 2048 | | LBFGS | 1 | 67 | 2.456124e-01 | 1.000000e+00 | 3.558719e-03 | 8.636596e-04 | 2048 | | LBFGS | 1 | 68 | 2.455980e-01 | 1.000000e+00 | 1.067616e-02 | 9.861527e-04 | 2048 | | LBFGS | 1 | 69 | 2.455780e-01 | 1.000000e+00 | 1.067616e-02 | 5.102487e-04 | 2048 | | LBFGS | 1 | 70 | 2.455633e-01 | 1.000000e+00 | 3.558719e-03 | 1.228077e-03 | 2048 | | LBFGS | 1 | 71 | 2.455449e-01 | 1.000000e+00 | 1.423488e-02 | 7.864590e-04 | 2048 | | LBFGS | 1 | 72 | 2.455261e-01 | 1.000000e+00 | 3.558719e-02 | 1.090815e-03 | 2048 | | LBFGS | 1 | 73 | 2.455142e-01 | 1.000000e+00 | 1.067616e-02 | 1.701506e-03 | 2048 | | LBFGS | 1 | 74 | 2.455075e-01 | 1.000000e+00 | 1.779359e-02 | 1.504577e-03 | 2048 | | LBFGS | 1 | 75 | 2.455008e-01 | 1.000000e+00 | 3.914591e-02 | 1.144021e-03 | 2048 | | LBFGS | 1 | 76 | 2.454943e-01 | 1.000000e+00 | 2.491103e-02 | 3.015254e-04 | 2048 | | LBFGS | 1 | 77 | 2.454918e-01 | 5.000000e-01 | 3.202847e-02 | 9.837523e-04 | 2048 | | LBFGS | 1 | 78 | 2.454870e-01 | 1.000000e+00 | 1.779359e-02 | 4.328953e-04 | 2048 | | LBFGS | 1 | 79 | 2.454865e-01 | 5.000000e-01 | 3.558719e-03 | 7.126815e-04 | 2048 | | LBFGS | 1 | 80 | 2.454775e-01 | 1.000000e+00 | 5.693950e-02 | 8.992562e-04 | 2048 | |=================================================================================================================| | Solver | Pass | Iteration | Objective | Step | Gradient | Relative | sum(beta~=0) | | | | | | | magnitude | change in Beta | | |=================================================================================================================| | LBFGS | 1 | 81 | 2.454686e-01 | 1.000000e+00 | 1.183730e-03 | 1.590246e-04 | 2048 | | LBFGS | 1 | 82 | 2.454612e-01 | 1.000000e+00 | 2.135231e-02 | 1.389570e-04 | 2048 | | LBFGS | 1 | 83 | 2.454506e-01 | 1.000000e+00 | 3.558719e-03 | 6.162089e-04 | 2048 | | LBFGS | 1 | 84 | 2.454436e-01 | 1.000000e+00 | 1.423488e-02 | 1.877414e-03 | 2048 | | LBFGS | 1 | 85 | 2.454378e-01 | 1.000000e+00 | 1.423488e-02 | 3.370852e-04 | 2048 | | LBFGS | 1 | 86 | 2.454249e-01 | 1.000000e+00 | 1.423488e-02 | 8.133615e-04 | 2048 | | LBFGS | 1 | 87 | 2.454101e-01 | 1.000000e+00 | 1.067616e-02 | 3.872088e-04 | 2048 | | LBFGS | 1 | 88 | 2.453963e-01 | 1.000000e+00 | 1.779359e-02 | 5.670260e-04 | 2048 | | LBFGS | 1 | 89 | 2.453866e-01 | 1.000000e+00 | 1.067616e-02 | 1.444984e-03 | 2048 | | LBFGS | 1 | 90 | 2.453821e-01 | 1.000000e+00 | 7.117438e-03 | 2.457270e-03 | 2048 | | LBFGS | 1 | 91 | 2.453790e-01 | 5.000000e-01 | 6.761566e-02 | 8.228766e-04 | 2048 | | LBFGS | 1 | 92 | 2.453603e-01 | 1.000000e+00 | 2.135231e-02 | 1.084233e-03 | 2048 | | LBFGS | 1 | 93 | 2.453540e-01 | 1.000000e+00 | 2.135231e-02 | 2.060005e-04 | 2048 | | LBFGS | 1 | 94 | 2.453482e-01 | 1.000000e+00 | 1.779359e-02 | 1.560883e-04 | 2048 | | LBFGS | 1 | 95 | 2.453461e-01 | 1.000000e+00 | 1.779359e-02 | 1.614693e-03 | 2048 | | LBFGS | 1 | 96 | 2.453371e-01 | 1.000000e+00 | 3.558719e-02 | 2.145835e-04 | 2048 | | LBFGS | 1 | 97 | 2.453305e-01 | 1.000000e+00 | 4.270463e-02 | 7.602088e-04 | 2048 | | LBFGS | 1 | 98 | 2.453283e-01 | 2.500000e-01 | 2.135231e-02 | 3.422253e-04 | 2048 | | LBFGS | 1 | 99 | 2.453246e-01 | 1.000000e+00 | 3.558719e-03 | 3.872561e-04 | 2048 | | LBFGS | 1 | 100 | 2.453214e-01 | 1.000000e+00 | 3.202847e-02 | 1.732237e-04 | 2048 | |=================================================================================================================| | Solver | Pass | Iteration | Objective | Step | Gradient | Relative | sum(beta~=0) | | | | | | | magnitude | change in Beta | | |=================================================================================================================| | LBFGS | 1 | 101 | 2.453168e-01 | 1.000000e+00 | 1.067616e-02 | 3.065286e-04 | 2048 | | LBFGS | 1 | 102 | 2.453155e-01 | 5.000000e-01 | 4.626335e-02 | 3.402368e-04 | 2048 | | LBFGS | 1 | 103 | 2.453136e-01 | 1.000000e+00 | 1.779359e-02 | 2.215029e-04 | 2048 | | LBFGS | 1 | 104 | 2.453119e-01 | 1.000000e+00 | 3.202847e-02 | 4.142355e-04 | 2048 | | LBFGS | 1 | 105 | 2.453093e-01 | 1.000000e+00 | 1.423488e-02 | 2.186007e-04 | 2048 | | LBFGS | 1 | 106 | 2.453090e-01 | 1.000000e+00 | 2.846975e-02 | 1.338602e-03 | 2048 | | LBFGS | 1 | 107 | 2.453048e-01 | 1.000000e+00 | 1.423488e-02 | 3.208296e-04 | 2048 | | LBFGS | 1 | 108 | 2.453040e-01 | 1.000000e+00 | 3.558719e-02 | 1.294488e-03 | 2048 | | LBFGS | 1 | 109 | 2.452977e-01 | 1.000000e+00 | 1.423488e-02 | 8.328380e-04 | 2048 | | LBFGS | 1 | 110 | 2.452934e-01 | 1.000000e+00 | 2.135231e-02 | 5.149259e-04 | 2048 | | LBFGS | 1 | 111 | 2.452886e-01 | 1.000000e+00 | 1.779359e-02 | 3.650664e-04 | 2048 | | LBFGS | 1 | 112 | 2.452854e-01 | 1.000000e+00 | 1.067616e-02 | 2.633981e-04 | 2048 | | LBFGS | 1 | 113 | 2.452836e-01 | 1.000000e+00 | 1.067616e-02 | 1.804300e-04 | 2048 | | LBFGS | 1 | 114 | 2.452817e-01 | 1.000000e+00 | 7.117438e-03 | 4.251642e-04 | 2048 | | LBFGS | 1 | 115 | 2.452741e-01 | 1.000000e+00 | 1.779359e-02 | 9.018440e-04 | 2048 | | LBFGS | 1 | 116 | 2.452691e-01 | 1.000000e+00 | 2.135231e-02 | 9.941716e-05 | 2048 | |=================================================================================================================|
Predict the test-set labels, construct a confusion matrix for the test set, and estimate the classification error for the test set.
UpdatedLabel = predict(UpdatedMdl,XTest); UpdatedConfusionTest = confusionchart(YTest,UpdatedLabel);

UpdatedL = loss(UpdatedMdl,XTest,YTest)
UpdatedL = 0.1284
The classification error decreases after resume updates the classification model with more iterations.
Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, either bad ('b') or good ('g').
load ionospherePartition the data set into training and test sets. Specify a 20% holdout sample for the test set.
rng('default') % For reproducibility Partition = cvpartition(Y,'Holdout',0.20); trainingInds = training(Partition); % Indices for the training set XTrain = X(trainingInds,:); YTrain = Y(trainingInds); testInds = test(Partition); % Indices for the test set XTest = X(testInds,:); YTest = Y(testInds);
Train a binary kernel classification model with relaxed convergence control training options by using the name-value pair arguments 'BetaTolerance' and 'GradientTolerance'.
[Mdl,FitInfo] = fitckernel(XTrain,YTrain,'Verbose',1, ... 'BetaTolerance',1e-1,'GradientTolerance',1e-1);
|=================================================================================================================| | Solver | Pass | Iteration | Objective | Step | Gradient | Relative | sum(beta~=0) | | | | | | | magnitude | change in Beta | | |=================================================================================================================| | LBFGS | 1 | 0 | 1.000000e+00 | 0.000000e+00 | 2.811388e-01 | | 0 | | LBFGS | 1 | 1 | 7.585395e-01 | 4.000000e+00 | 3.594306e-01 | 1.000000e+00 | 2048 | | LBFGS | 1 | 2 | 7.160994e-01 | 1.000000e+00 | 2.028470e-01 | 6.923988e-01 | 2048 | | LBFGS | 1 | 3 | 6.825272e-01 | 1.000000e+00 | 2.846975e-02 | 2.388909e-01 | 2048 | |=================================================================================================================|
Mdl is a ClassificationKernel model.
Predict the test-set labels, construct a confusion matrix for the test set, and estimate the classification error for the test set
label = predict(Mdl,XTest); ConfusionTest = confusionchart(YTest,label);
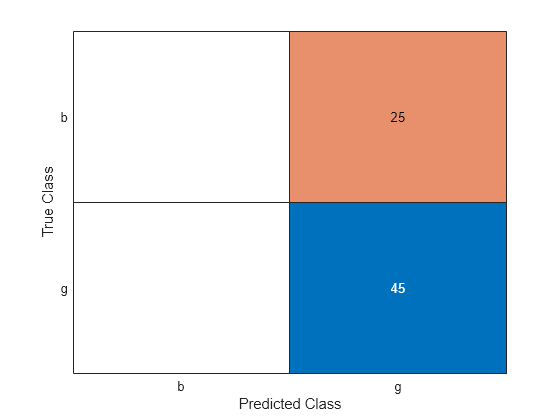
L = loss(Mdl,XTest,YTest)
L = 0.3594
Mdl misclassifies all bad radar returns as good returns.
Continue training by using resume with modified convergence control training options.
[UpdatedMdl,UpdatedFitInfo] = resume(Mdl,XTrain,YTrain, ... 'BetaTolerance',1e-2,'GradientTolerance',1e-2);
|=================================================================================================================| | Solver | Pass | Iteration | Objective | Step | Gradient | Relative | sum(beta~=0) | | | | | | | magnitude | change in Beta | | |=================================================================================================================| | LBFGS | 1 | 0 | 6.825272e-01 | 0.000000e+00 | 2.846975e-02 | | 2048 | | LBFGS | 1 | 1 | 6.692805e-01 | 2.000000e+00 | 2.846975e-02 | 1.389258e-01 | 2048 | | LBFGS | 1 | 2 | 6.466824e-01 | 1.000000e+00 | 2.348754e-01 | 4.149425e-01 | 2048 | | LBFGS | 1 | 3 | 5.441382e-01 | 2.000000e+00 | 1.743772e-01 | 5.344538e-01 | 2048 | | LBFGS | 1 | 4 | 5.222333e-01 | 1.000000e+00 | 3.309609e-01 | 7.530878e-01 | 2048 | | LBFGS | 1 | 5 | 3.776579e-01 | 1.000000e+00 | 1.103203e-01 | 6.532621e-01 | 2048 | | LBFGS | 1 | 6 | 3.523520e-01 | 1.000000e+00 | 5.338078e-02 | 1.384232e-01 | 2048 | | LBFGS | 1 | 7 | 3.422319e-01 | 5.000000e-01 | 3.202847e-02 | 9.703897e-02 | 2048 | | LBFGS | 1 | 8 | 3.341895e-01 | 1.000000e+00 | 3.202847e-02 | 5.009485e-02 | 2048 | | LBFGS | 1 | 9 | 3.199302e-01 | 1.000000e+00 | 4.982206e-02 | 8.038014e-02 | 2048 | | LBFGS | 1 | 10 | 3.017904e-01 | 1.000000e+00 | 1.423488e-02 | 2.845012e-01 | 2048 | | LBFGS | 1 | 11 | 2.853480e-01 | 1.000000e+00 | 3.558719e-02 | 9.799137e-02 | 2048 | | LBFGS | 1 | 12 | 2.753979e-01 | 1.000000e+00 | 3.914591e-02 | 9.975305e-02 | 2048 | | LBFGS | 1 | 13 | 2.647492e-01 | 1.000000e+00 | 3.914591e-02 | 9.713710e-02 | 2048 | | LBFGS | 1 | 14 | 2.639242e-01 | 1.000000e+00 | 1.423488e-02 | 6.721803e-02 | 2048 | | LBFGS | 1 | 15 | 2.617385e-01 | 1.000000e+00 | 1.779359e-02 | 2.625089e-02 | 2048 | | LBFGS | 1 | 16 | 2.598600e-01 | 1.000000e+00 | 7.117438e-02 | 3.338724e-02 | 2048 | | LBFGS | 1 | 17 | 2.594176e-01 | 1.000000e+00 | 1.067616e-02 | 2.441171e-02 | 2048 | | LBFGS | 1 | 18 | 2.579350e-01 | 1.000000e+00 | 3.202847e-02 | 2.979246e-02 | 2048 | | LBFGS | 1 | 19 | 2.570669e-01 | 1.000000e+00 | 1.779359e-02 | 4.432998e-02 | 2048 | | LBFGS | 1 | 20 | 2.552954e-01 | 1.000000e+00 | 1.769940e-03 | 1.899895e-02 | 2048 | |=================================================================================================================|
Predict the test-set labels, construct a confusion matrix for the test set, and estimate the classification error for the test set.
UpdatedLabel = predict(UpdatedMdl,XTest); UpdatedConfusionTest = confusionchart(YTest,UpdatedLabel);
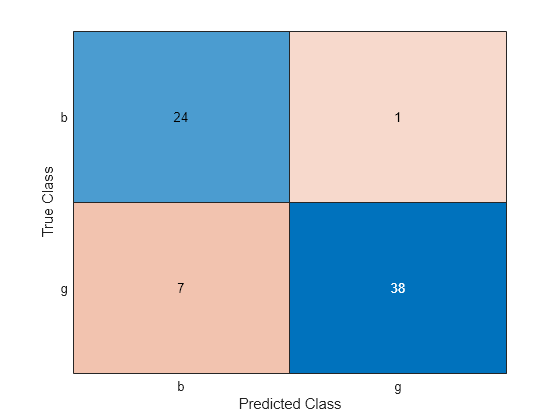
UpdatedL = loss(UpdatedMdl,XTest,YTest)
UpdatedL = 0.1140
The classification error decreases after resume updates the classification model with smaller convergence tolerances.
Display the outputs FitInfo and UpdatedFitInfo.
FitInfo
FitInfo = struct with fields:
Solver: 'LBFGS-fast'
LossFunction: 'hinge'
Lambda: 0.0036
BetaTolerance: 0.1000
GradientTolerance: 0.1000
ObjectiveValue: 0.6825
GradientMagnitude: 0.0285
RelativeChangeInBeta: 0.2389
FitTime: 0.0351
History: [1×1 struct]
UpdatedFitInfo
UpdatedFitInfo = struct with fields:
Solver: 'LBFGS-fast'
LossFunction: 'hinge'
Lambda: 0.0036
BetaTolerance: 0.0100
GradientTolerance: 0.0100
ObjectiveValue: 0.2553
GradientMagnitude: 0.0018
RelativeChangeInBeta: 0.0190
FitTime: 0.0590
History: [1×1 struct]
Both trainings terminate because the software satisfies the absolute gradient tolerance.
Plot the gradient magnitude versus the number of iterations by using UpdatedFitInfo.History.GradientMagnitude. Note that the History field of UpdatedFitInfo includes the information in the History field of FitInfo.
semilogy(UpdatedFitInfo.History.GradientMagnitude,'o-') ax = gca; ax.XTick = 1:25; ax.XTickLabel = UpdatedFitInfo.History.IterationNumber; grid on xlabel('Number of Iterations') ylabel('Gradient Magnitude')
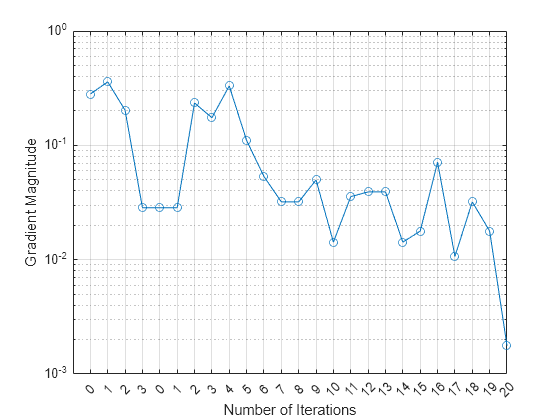
The first training terminates after three iterations because the gradient magnitude becomes less than 1e-1. The second training terminates after 20 iterations because the gradient magnitude becomes less than 1e-2.
Input Arguments
Binary kernel classification model, specified as a ClassificationKernel model object. You can create a
ClassificationKernel model object using fitckernel.
Predictor data used to train Mdl, specified as an
n-by-p numeric matrix, where
n is the number of observations and
p is the number of predictors.
Data Types: single | double
Class labels used to train Mdl, specified as a
categorical, character, or string array, logical or numeric vector, or cell
array of character vectors.
Data Types: categorical | char | string | logical | single | double | cell
Sample data used to train Mdl, specified as a table.
Each row of Tbl corresponds to one observation, and
each column corresponds to one predictor variable. Optionally,
Tbl can contain additional columns for the response
variable and observation weights. Tbl must contain all
of the predictors used to train Mdl. Multicolumn
variables and cell arrays other than cell arrays of character vectors are
not allowed.
If you trained Mdl using sample data contained in a
table, then the input data for resume must also be in a
table.
Note
resume should run only on the same training data and
observation weights used to train Mdl. The
resume function uses the same training options used to
train Mdl, including feature expansion.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: UpdatedMdl = resume(Mdl,X,Y,'GradientTolerance',1e-5)
resumes training with the same options used to train Mdl, except
the absolute gradient tolerance.
Observation weights used to train Mdl, specified
as the comma-separated pair consisting of 'Weights'
and a numeric vector or the name of a variable in
Tbl.
If
Weightsis a numeric vector, then the size ofWeightsmust be equal to the number of rows inXorTbl.If
Weightsis the name of a variable inTbl, you must specifyWeightsas a character vector or string scalar. For example, if the weights are stored asTbl.W, then specifyWeightsas'W'. Otherwise, the software treats all columns ofTbl, includingTbl.W, as predictors.
If you supply weights, resume normalizes the
weights to sum up to the value of the prior probability in the
respective class.
Data Types: double | single | char | string
Relative tolerance on the linear coefficients and the bias term (intercept), specified as a nonnegative scalar.
Let , that is, the vector of the coefficients and the bias term at optimization iteration t. If , then optimization terminates.
If you also specify GradientTolerance, then optimization terminates when the software satisfies either stopping criterion.
By default, the value is the same BetaTolerance
value used to train Mdl.
Example: 'BetaTolerance',1e-6
Data Types: single | double
Absolute gradient tolerance, specified as a nonnegative scalar.
Let be the gradient vector of the objective function with respect to the coefficients and bias term at optimization iteration t. If , then optimization terminates.
If you also specify BetaTolerance, then optimization terminates when the
software satisfies either stopping criterion.
By default, the value is the same GradientTolerance
value used to train Mdl.
Example: 'GradientTolerance',1e-5
Data Types: single | double
Maximum number of additional optimization iterations, specified as the
comma-separated pair consisting of 'IterationLimit'
and a positive integer.
The default value is 1000 if the transformed data fits in memory
(Mdl.ModelParameters.BlockSize), which you
specify by using the name-value pair argument when training
Mdl. Otherwise, the default value is
100.
Note that the default value is not the value used to train
Mdl.
Example: 'IterationLimit',500
Data Types: single | double
Output Arguments
Updated kernel classification model, returned as a ClassificationKernel model object.
Optimization details, returned as a structure array including fields described in this table. The fields contain final values or name-value pair argument specifications.
| Field | Description |
|---|---|
Solver |
Objective function minimization technique:
|
LossFunction | Loss function. Either 'hinge' or
'logit' depending on the type of
linear classification model. See Learner of
fitckernel. |
Lambda | Regularization term strength. See Lambda of
fitckernel. |
BetaTolerance | Relative tolerance on the linear coefficients and the
bias term. See BetaTolerance. |
GradientTolerance | Absolute gradient tolerance. See
GradientTolerance. |
ObjectiveValue | Value of the objective function when optimization terminates. The classification loss plus the regularization term compose the objective function. |
GradientMagnitude | Infinite norm of the gradient vector of the objective
function when optimization terminates. See
GradientTolerance. |
RelativeChangeInBeta | Relative changes in the linear coefficients and the bias
term when optimization terminates. See
BetaTolerance. |
FitTime | Elapsed, wall-clock time (in seconds) required to fit the model to the data. |
History | History of optimization information. This field also
includes the optimization information from training
Mdl. This field is empty
([]) if you specify
'Verbose',0 when training
Mdl. For details, see Verbose and Algorithms of fitckernel. |
To access fields, use dot notation. For example, to access the vector of
objective function values for each iteration, enter
FitInfo.ObjectiveValue in the Command Window.
A good practice is to examine FitInfo to assess whether
convergence is satisfactory.
More About
Random feature expansion, such as Random Kitchen Sinks [1] or Fastfood [2], is a scheme to approximate Gaussian kernels of the kernel classification algorithm to use for big data in a computationally efficient way. Random feature expansion is more practical for big data applications that have large training sets, but can also be applied to smaller data sets that fit in memory.
The kernel classification algorithm searches for an optimal hyperplane that separates the data into two classes after mapping features into a high-dimensional space. Nonlinear features that are not linearly separable in a low-dimensional space can be separable in the expanded high-dimensional space. All the calculations for hyperplane classification use only dot products. You can obtain a nonlinear classification model by replacing the dot product x1x2' with the nonlinear kernel function , where xi is the ith observation (row vector) and φ(xi) is a transformation that maps xi to a high-dimensional space (called the “kernel trick”). However, evaluating G(x1,x2) (Gram matrix) for each pair of observations is computationally expensive for a large data set (large n).
The random feature expansion scheme finds a random transformation so that its dot product approximates the Gaussian kernel. That is,
where T(x) maps x in to a high-dimensional space (). The Random Kitchen Sinks scheme uses the random transformation
where is a sample drawn from and σ is a kernel scale. This scheme requires O(mp) computation and storage.
The Fastfood scheme introduces another random
basis V instead of Z using Hadamard matrices combined
with Gaussian scaling matrices. This random basis reduces the computation cost to O(mlogp) and reduces storage to O(m).
The fitckernel function uses the Fastfood scheme for random feature expansion and uses linear classification to train a Gaussian kernel classification model. Unlike solvers in the fitcsvm function, which require computation of the n-by-n Gram matrix, the solver in fitckernel only needs to form a matrix of size n-by-m, with m typically much less than n for big data.
References
[1] Rahimi, A., and B. Recht. “Random Features for Large-Scale Kernel Machines.” Advances in Neural Information Processing Systems. Vol. 20, 2008, pp. 1177–1184.
[2] Le, Q., T. Sarlós, and A. Smola. “Fastfood — Approximating Kernel Expansions in Loglinear Time.” Proceedings of the 30th International Conference on Machine Learning. Vol. 28, No. 3, 2013, pp. 244–252.
[3] Huang, P. S., H. Avron, T. N. Sainath, V. Sindhwani, and B. Ramabhadran. “Kernel methods match Deep Neural Networks on TIMIT.” 2014 IEEE International Conference on Acoustics, Speech and Signal Processing. 2014, pp. 205–209.
Extended Capabilities
The
resume function supports tall arrays with the following usage
notes and limitations:
resumedoes not support talltabledata.The default value for the
'IterationLimit'name-value pair argument is relaxed to 20 when working with tall arrays.resumeuses a block-wise strategy. For details, see Algorithms offitckernel.
For more information, see Tall Arrays.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2017bresume fully supports GPU arrays.
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)