incrementalRegressionLinear
Linear regression model for incremental learning
Description
incrementalRegressionLinear creates an incrementalRegressionLinear model object, which represents an incremental linear model for regression problems. Supported learners include support vector machine (SVM) and least squares.
Unlike other Statistics and Machine Learning Toolbox™ model objects, incrementalRegressionLinear can be called directly. Also, you can specify learning options, such as performance metrics configurations, parameter values, and the objective solver, before fitting the model to data. After you create an incrementalRegressionLinear object, it is prepared for incremental learning.
incrementalRegressionLinear is best suited for incremental learning. For a traditional approach to training an SVM or linear regression model (such as creating a model by fitting it to data, performing cross-validation, tuning hyperparameters, and so on), see fitrsvm or fitrlinear.
Creation
You can create an incrementalRegressionLinear model object in several ways:
Call the function directly — Configure incremental learning options, or specify initial values for linear model parameters and hyperparameters, by calling
incrementalRegressionLineardirectly. This approach is best when you do not have data yet or you want to start incremental learning immediately.Convert a traditionally trained model — To initialize an linear regression model for incremental learning using the model coefficients and hyperparameters of a trained model object, you can convert the traditionally trained model to an
incrementalRegressionLinearmodel object by passing it to theincrementalLearnerfunction. This table contains links to the appropriate reference pages.Convertible Model Object Conversion Function RegressionSVMorCompactRegressionSVMincrementalLearnerRegressionLinearincrementalLearnerCall an incremental learning function —
fit,updateMetrics, andupdateMetricsAndFitaccept a configuredincrementalRegressionLinearmodel object and data as input, and return anincrementalRegressionLinearmodel object updated with information learned from the input model and data.
Description
Mdl = incrementalRegressionLinear()Mdl.
Properties of a default model contain placeholders for unknown model parameters. You must
train a default model before you can track its performance or generate predictions from
it.
Mdl = incrementalRegressionLinear(Name=Value)incrementalRegressionLinear(Beta=[0.1
0.3],Bias=1,MetricsWarmupPeriod=100) sets the vector of linear model
coefficients β to [0.1 0.3], the bias
β0 to 1, and the metrics
warm-up period to 100.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: Standardize=true standardizes the predictor data using the
predictor means and standard deviations estimated during the estimation
period.
Model performance metrics to track during incremental learning, specified as a
built-in loss function name, string vector of names, function handle
(@metricName), structure array of function handles, or cell
vector of names, function handles, or structure arrays.
When Mdl is warm (see IsWarm), updateMetrics and updateMetricsAndFit track performance metrics in the Metrics property of Mdl.
The following table lists the built-in loss function names and which learners,
specified in Learner, support them. You can specify
more than one loss function by using a string vector.
| Name | Description | Learner Supporting Metric |
|---|---|---|
"epsiloninsensitive" | Epsilon insensitive loss | 'svm' |
"mse" | Weighted mean squared error | 'svm' and 'leastsquares' |
For more details on the built-in loss functions, see loss.
Example: 'Metrics',["epsiloninsensitive" "mse"]
To specify a custom function that returns a performance metric, use function handle notation. The function must have this form:
metric = customMetric(Y,YFit)
The output argument
metricis an n-by-1 numeric vector, where each element is the loss of the corresponding observation in the data processed by the incremental learning functions during a learning cycle.You specify the function name (
customMetric).Yis a length n numeric vector of observed responses, where n is the sample size.YFitis a length n numeric vector of corresponding predicted responses.
To specify multiple custom metrics and assign a custom name to each, use a structure array. To specify a combination of built-in and custom metrics, use a cell vector.
Example: 'Metrics',struct('Metric1',@customMetric1,'Metric2',@customMetric2)
Example: 'Metrics',{@customMetric1 @customMetric2 'mse'
struct('Metric3',@customMetric3)}
updateMetrics and updateMetricsAndFit store specified metrics in a table in the property Metrics. The data type of Metrics determines the row names of the table.
'Metrics' Value Data Type | Description of Metrics Property Row Name | Example |
|---|---|---|
| String or character vector | Name of corresponding built-in metric | Row name for "epsiloninsensitive" is "EpsilonInsensitiveLoss" |
| Structure array | Field name | Row name for struct('Metric1',@customMetric1) is "Metric1" |
| Function handle to function stored in a program file | Name of function | Row name for @customMetric is "customMetric" |
| Anonymous function | CustomMetric_, where Metrics | Row name for @(Y,YFit)customMetric(Y,YFit)... is CustomMetric_1 |
By default:
Metricsis"epsiloninsensitive"ifLearneris'svm'.Metricsis"mse"ifLearneris'leastsquares'.
For more details on performance metrics options, see Performance Metrics.
Data Types: char | string | struct | cell | function_handle
Flag to standardize the predictor data, specified as a value in this table.
| Value | Description |
|---|---|
'auto' | incrementalRegressionLinear determines whether the predictor
variables need to be standardized. See Standardize Data. |
true | The software standardizes the predictor data. For more details, see Standardize Data. |
false | The software does not standardize the predictor data. |
Example: 'Standardize',true
Data Types: logical | char | string
Flag for shuffling the observations at each iteration, specified as a value in this table.
| Value | Description |
|---|---|
true | The software shuffles the observations in an incoming chunk of
data before the fit function fits the model. This
action reduces bias induced by the sampling scheme. |
false | The software processes the data in the order received. |
This option is valid only when Solver is
'scale-invariant'. When Solver is
'sgd' or 'asgd', the software always
shuffles the observations in an incoming chunk of data before processing the
data.
Example: 'Shuffle',false
Data Types: logical
Properties
You can set most properties by using name-value argument syntax only when you call
incrementalRegressionLinear. You can set some properties when you call
incrementalLearner to convert a traditionally trained model. You cannot
set the properties FittedLoss,
NumTrainingObservations, Mu,
Sigma, SolverOptions, and
IsWarm.
Regression Model Parameters
This property is read-only.
Linear model coefficients β, specified as a NumPredictors-by-1 numeric vector.
Incremental fitting functions estimate Beta during training. The
default initial Beta value depends on how you create the model:
If you convert a traditionally trained model to create
Mdl, the initial value is specified by the corresponding property of the traditionally trained model.Otherwise, the initial value is
zeros(NumPredictors,1).
Data Types: single | double
This property is read-only.
Model intercept β0, or bias term, specified as a numeric scalar.
Incremental fitting functions estimate Bias during training. The
default initial Bias value depends on how you create the model:
If you convert a traditionally trained model to create
Mdl, the initial value is specified by the corresponding property of the traditionally trained model.Otherwise, the initial value is
0.
Data Types: single | double
This property is read-only.
Half of the width of the epsilon insensitive band, specified as
'auto' or a nonnegative scalar. incrementalRegressionLinear
stores the Epsilon value as a numeric scalar.
If you specify 'auto' when you call
incrementalRegressionLinear, incremental fitting functions estimate
Epsilon during the estimation period, specified by EstimationPeriod, using
this procedure:
If
iqr(Y)≠ 0,Epsilonisiqr(Y)/13.49, whereYis the estimation period response data.If
iqr(Y)= 0 or before you fitMdlto data,Epsilonis0.1.
The default Epsilon value depends on how you create the model:
If you convert a traditionally trained SVM regression model (
Learneris'svm'),Epsilonis specified by the corresponding property of the traditionally trained model.Otherwise, the default value is
'auto'.
If Learner is 'leastsquares', you cannot
set Epsilon and its value is NaN.
Data Types: single | double
This property is read-only.
Loss function used to fit the linear model, specified as
'epsiloninsensitive' or 'mse'.
| Value | Algorithm | Loss Function | Learner Value |
|---|---|---|---|
'epsiloninsensitive' | Support vector machine regression | Epsilon insensitive: | 'svm' |
'mse' | Linear regression through ordinary least squares | Mean squared error (MSE): | 'leastsquares' |
This property is read-only.
Linear regression model type, specified as 'svm' or
'leastsquares'. incrementalRegressionLinear stores the
Learner value as a character vector.
In the following table,
β is
Beta.x is an observation from p predictor variables.
β0 is
Bias.
| Value | Algorithm | Loss Function | FittedLoss Value |
|---|---|---|---|
'svm' | Support vector machine regression | Epsilon insensitive: | 'epsiloninsensitive' |
'leastsquares' | Linear regression through ordinary least squares | Mean squared error (MSE): | 'mse' |
The default Learner value depends on how you create the model:
If you convert a traditionally trained model to create
Mdl:Learneris'svm'when the traditionally trained model isRegressionSVMorCompactRegressionSVM.Learneris specified by the corresponding property of the traditionally trained model when the traditionally trained model isRegressionLinear.
Otherwise, the default value is
'svm'.
Data Types: char | string
This property is read-only.
Number of predictor variables, specified as a nonnegative numeric scalar.
The default NumPredictors value depends on how you create the model:
If you convert a traditionally trained model to create
Mdl,NumPredictorsis specified by the corresponding property of the traditionally trained model.If you create
Mdlby callingincrementalRegressionLineardirectly, you can specifyNumPredictorsby using name-value argument syntax. If you do not specify the value, then the default value is0, and incremental fitting functions inferNumPredictorsfrom the predictor data during training.
Data Types: double
This property is read-only.
Number of observations fit to the incremental model Mdl, specified as a nonnegative numeric scalar. NumTrainingObservations increases when you pass Mdl and training data to fit or updateMetricsAndFit.
Note
If you convert a traditionally trained model to create Mdl, incrementalRegressionLinear does not add the number of observations fit to the traditionally trained model to NumTrainingObservations.
Data Types: double
This property is read-only.
Response transformation function, specified as 'none' or a
function handle. incrementalRegressionLinear stores the
ResponseTransform value as a character vector or function
handle.
ResponseTransform describes how incremental learning
functions transform raw response values.
For a MATLAB® function or a function that you define, enter its function handle; for
example, 'ResponseTransform',@function, where
function accepts an
n-by-1 vector (the original responses) and returns a vector of the
same length (the transformed responses).
The default ResponseTransform value depends on how you create
the model:
If you convert a traditionally trained model to create
Mdl,ResponseTransformis specified by the corresponding property of the traditionally trained model.Otherwise, the default value is
"none".
Data Types: char | string | function_handle
Training Parameters
This property is read-only.
Number of observations processed by the incremental model to estimate hyperparameters before training or tracking performance metrics, specified as a nonnegative integer.
Note
If
Mdlis prepared for incremental learning (all hyperparameters required for training are specified),incrementalRegressionLinearforcesEstimationPeriodto0.If
Mdlis not prepared for incremental learning,incrementalRegressionLinearsetsEstimationPeriodto1000.
For more details, see Estimation Period.
Data Types: single | double
This property is read-only.
Linear model intercept inclusion flag, specified as true or
false.
| Value | Description |
|---|---|
true | incrementalRegressionLinear includes the bias term
β0 in the linear model, which
incremental fitting functions fit to data. |
false | incrementalRegressionLinear sets
β0 = 0. |
If Bias ≠ 0, FitBias must be
true. In other words, incrementalRegressionLinear does not
support an equality constraint on β0.
The default FitBias value depends on how you create the model:
If you convert a traditionally trained linear regression model (
RegressionLinear) to createMdl,FitBiasis specified by theFitBiasvalue of theModelParametersproperty of the traditionally trained model.Otherwise, the default value is
true.
Data Types: logical
This property is read-only.
Predictor means, specified as a numeric vector.
If Mu is an empty array [] and you specify 'Standardize',true, incremental fitting functions set Mu to the predictor variable means estimated during the estimation period specified by EstimationPeriod.
You cannot specify Mu directly.
Data Types: single | double
This property is read-only.
Predictor standard deviations, specified as a numeric vector.
If Sigma is an empty array [] and you specify 'Standardize',true, incremental fitting functions set Sigma to the predictor variable standard deviations estimated during the estimation period specified by EstimationPeriod.
You cannot specify Sigma directly.
Data Types: single | double
This property is read-only.
Objective function minimization technique, specified as
'scale-invariant', 'sgd', or
'asgd'. incrementalRegressionLinear stores the
Solver value as a character vector.
| Value | Description | Notes |
|---|---|---|
'scale-invariant' | Adaptive scale-invariant solver for incremental learning [1] |
|
'sgd' | Stochastic gradient descent (SGD) [3][2] |
|
'asgd' | Average stochastic gradient descent (ASGD) [4] |
|
The default Solver value depends on how you create the model:
If you create
Mdlby callingincrementalRegressionLineardirectly, the default value is'scale-invariant'.If you convert a traditionally trained linear regression model (
RegressionLinear) to createMdl, and the traditionally trained model'sRegularizationproperty is'ridge (L2)'andModelParameters.Solveris'sgd'or'asgd',Solveris specified by theSolvervalue of theModelParametersproperty of the traditionally trained model.Otherwise, the
Solvername-value argument of theincrementalLearnerfunction sets this property. The default value of the argument is'scale-invariant'.
Data Types: char | string
This property is read-only.
Objective solver configurations, specified as a structure array. The fields of
SolverOptions are properties specific to the specified solver
Solver.
Data Types: struct
SGD and ASGD Solver Parameters
This property is read-only.
Mini-batch size, specified as a positive integer. At each learning cycle during
training, incrementalRegressionLinear uses BatchSize
observations to compute the subgradient.
The number of observations for the last mini-batch (last learning cycle in each
function call of fit or updateMetricsAndFit) can
be smaller than BatchSize. For example, if you supply 25
observations to fit or updateMetricsAndFit,
the function uses 10 observations for the first two learning cycles and 5 observations
for the last learning cycle.
The default BatchSize value depends on how you create the model:
If you create
Mdlby callingincrementalRegressionLineardirectly, the default value is10.If you convert a traditionally trained linear regression model (
RegressionLinear) to createMdl, and the traditionally trained model'sRegularizationproperty is'ridge (L2)'andModelParameters.Solveris'sgd'or'asgd',BatchSizeis specified by theBatchSizevalue of theModelParametersproperty of the traditionally trained model.Otherwise, the
BatchSizename-value argument of theincrementalLearnerfunction sets this property. The default value of the argument is10.
Data Types: single | double
This property is read-only.
Ridge (L2) regularization term strength, specified as a nonnegative scalar.
The default Lambda value depends on how you create the model:
If you create
Mdlby callingincrementalRegressionLineardirectly, the default value is1e-5.If you convert a traditionally trained linear regression model (
RegressionLinear) to createMdl, and the traditionally trained model'sRegularizationproperty is'ridge (L2)'andModelParameters.Solveris'sgd'or'asgd',Lambdais specified by the corresponding property of the traditionally trained model.Otherwise, the
Lambdaname-value argument of theincrementalLearnerfunction sets this property. The default value of the argument is1e-5.
Data Types: double | single
This property is read-only.
Initial learning rate, specified as 'auto' or a positive
scalar. incrementalRegressionLinear stores the LearnRate value
as a positive scalar.
The learning rate controls the optimization step size by scaling the objective
subgradient. LearnRate specifies an initial value for the learning
rate, and LearnRateSchedule determines
the learning rate for subsequent learning cycles.
When you specify 'auto':
The initial learning rate is
0.7.If
EstimationPeriod>0,fitandupdateMetricsAndFitchange the rate to1/sqrt(1+max(sum(X.^2,obsDim)))at the end ofEstimationPeriod. When the observations are the columns of the predictor dataXcollected during the estimation period, theobsDimvalue is1; otherwise, the value is2.
The default LearnRate value depends on how you create the model:
If you create
Mdlby callingincrementalRegressionLineardirectly, the default value is'auto'.If you convert a traditionally trained linear regression model (
RegressionLinear) to createMdl, and the traditionally trained model'sRegularizationproperty is'ridge (L2)'andModelParameters.Solveris'sgd'or'asgd',LearnRateis specified by theLearnRatevalue of theModelParametersproperty of the traditionally trained model.Otherwise, the
LearnRatename-value argument of theincrementalLearnerfunction sets this property. The default value of the argument is'auto'.
Example: 'LearnRate',0.001
Data Types: single | double | char | string
This property is read-only.
Learning rate schedule, specified as a value in this table, where LearnRate specifies
the initial learning rate ɣ0.
incrementalRegressionLinear stores the LearnRateSchedule
value as a character vector.
| Value | Description |
|---|---|
'constant' | The learning rate is ɣ0 for all learning cycles. |
'decaying' | The learning rate at learning cycle t is
|
The default LearnRateSchedule value depends on how you
create the model:
If you convert a traditionally trained model to create
Mdl, theLearnRateSchedulename-value argument of theincrementalLearnerfunction sets this property. The default value of the argument is'decaying'.Otherwise, the default value is
'decaying'.
Data Types: char | string
Performance Metrics Parameters
This property is read-only.
Flag indicating whether the incremental model tracks performance metrics, specified as
logical 0 (false) or 1
(true).
The incremental model Mdl is warm
(IsWarm becomes true) after incremental
fitting functions fit (EstimationPeriod +
MetricsWarmupPeriod) observations to the incremental
model.
| Value | Description |
|---|---|
true or 1 | The incremental model Mdl is warm. Consequently,
updateMetrics and
updateMetricsAndFit track performance metrics
in the Metrics property of
Mdl. |
false or 0 | updateMetrics and
updateMetricsAndFit do not track performance
metrics. |
Data Types: logical
This property is read-only.
Model performance metrics updated during incremental learning by
updateMetrics and updateMetricsAndFit,
specified as a table with two columns and m rows, where
m is the number of metrics specified by the Metrics name-value
argument.
The columns of Metrics are labeled Cumulative and Window.
Cumulative: Elementjis the model performance, as measured by metricj, from the time the model became warm (IsWarmis1).Window: Elementjis the model performance, as measured by metricj, evaluated over all observations within the window specified by theMetricsWindowSizeproperty. The software updatesWindowafter it processesMetricsWindowSizeobservations.
Rows are labeled by the specified metrics. For details, see the
Metrics name-value argument of
incrementalLearner or incrementalRegressionLinear.
Data Types: table
This property is read-only.
Number of observations the incremental model must be fit to before it tracks performance metrics in its Metrics property, specified as a nonnegative integer.
The default MetricsWarmupPeriod value depends on how you create
the model:
If you convert a traditionally trained model to create
Mdl, theMetricsWarmupPeriodname-value argument of theincrementalLearnerfunction sets this property. The default value of the argument is0.Otherwise, the default value is
1000.
For more details, see Performance Metrics.
Data Types: single | double
This property is read-only.
Number of observations to use to compute window performance metrics, specified as a positive integer.
The default MetricsWindowSize value depends on how you create the model:
If you convert a traditionally trained model to create
Mdl, theMetricsWindowSizename-value argument of theincrementalLearnerfunction sets this property. The default value of the argument is200.Otherwise, the default value is
200.
For more details on performance metrics options, see Performance Metrics.
Data Types: single | double
Object Functions
fit | Train linear model for incremental learning |
updateMetricsAndFit | Update performance metrics in linear incremental learning model given new data and train model |
updateMetrics | Update performance metrics in linear incremental learning model given new data |
loss | Loss of linear incremental learning model on batch of data |
predict | Predict responses for new observations from linear incremental learning model |
perObservationLoss | Per observation regression error of model for incremental learning |
reset | Reset incremental regression model |
Examples
Create a default incremental linear model for regression.
Mdl = incrementalRegressionLinear()
Mdl =
incrementalRegressionLinear
IsWarm: 0
Metrics: [1×2 table]
ResponseTransform: 'none'
Beta: [0×1 double]
Bias: 0
Learner: 'svm'
Properties, Methods
Mdl.EstimationPeriod
ans = 1000
Mdl is an incrementalRegressionLinear model object. All its properties are read-only.
Mdl must be fit to data before you can use it to perform any other operations. The software sets the estimation period to 1000 because half the width of the epsilon insensitive band Epsilon is unknown. You can set Epsilon to a positive floating-point scalar by using the Epsilon name-value argument. This action results in a default estimation period of 0.
Load the robot arm data set.
load robotarmFor details on the data set, enter Description at the command line.
Fit the incremental model to the training data by using the updateMetricsAndFit function. To simulate a data stream fit the model in chunks of 50 observations at a time. At each iteration:
Process 50 observations.
Overwrite the previous incremental model with a new one fitted to the incoming observations.
Store , the cumulative metrics, and the window metrics to see how they evolve during incremental learning.
% Preallocation n = numel(ytrain); numObsPerChunk = 50; nchunk = floor(n/numObsPerChunk); ei = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]); beta1 = zeros(nchunk+1,1); % Incremental fitting rng("default"); % For reproducibility for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; Mdl = updateMetricsAndFit(Mdl,Xtrain(idx,:),ytrain(idx)); ei{j,:} = Mdl.Metrics{"EpsilonInsensitiveLoss",:}; beta1(j + 1) = Mdl.Beta(1); end
Mdl is an incrementalRegressionLinear model object trained on all the data in the stream. While updateMetricsAndFit processes the first 1000 observations, it stores the response values to estimate Epsilon; the function does not fit the coefficients until after this estimation period. During incremental learning and after the model is warmed up, updateMetricsAndFit checks the performance of the model on the incoming observations, and then fits the model to those observations.
To see how the performance metrics and evolve during training, plot them on separate tiles.
t = tiledlayout(2,1); nexttile plot(beta1) ylabel('\beta_1') xlim([0 nchunk]) xline(Mdl.EstimationPeriod/numObsPerChunk,'r-.') nexttile h = plot(ei.Variables); xlim([0 nchunk]) ylabel('Epsilon Insensitive Loss') xline(Mdl.EstimationPeriod/numObsPerChunk,'r-.') xline((Mdl.EstimationPeriod + Mdl.MetricsWarmupPeriod)/numObsPerChunk,'g-.') legend(h,ei.Properties.VariableNames) xlabel(t,'Iteration')

The plot suggests that updateMetricsAndFit does the following:
After the estimation period (first 20 iterations), fit during all incremental learning iterations.
Compute the performance metrics after the metrics warm-up period only.
Compute the cumulative metrics during each iteration.
Compute the window metrics after processing 500 observations (4 iterations).
Prepare an incremental regression learner by specifying a metrics warm-up period, during which the updateMetricsAndFit function only fits the model. Specify a metrics window size of 500 observations. Train the model by using SGD, and adjust the SGD batch size, learning rate, and regularization parameter.
Load the robot arm data set.
load robotarm
n = numel(ytrain);For details on the data set, enter Description at the command line.
Create an incremental linear model for regression. Configure the model as follows:
Specify the SGD solver.
Assume that these settings work well for the problem: a ridge regularization parameter value of 0.001, SGD batch size of 20, learning rate of 0.002, and half the width of the epsilon insensitive band for SVM of 0.05.
Specify that the incremental fitting functions process the raw (unstandardized) predictor data.
Specify a metrics warm-up period of 1000 observations.
Specify a metrics window size of 500 observations.
Track the epsilon insensitive loss, MSE, and mean absolute error (MAE) to measure the performance of the model. The software supports epsilon insensitive loss and MSE. Create an anonymous function that measures the absolute error of each new observation. Create a structure array containing the name
MeanAbsoluteErrorand its corresponding function.
maefcn = @(z,zfit)abs(z - zfit); maemetric = struct("MeanAbsoluteError",maefcn); Mdl = incrementalRegressionLinear('Epsilon',0.05, ... 'Solver','sgd','Lambda',0.001,'BatchSize',20,'LearnRate',0.002, ... 'Standardize',false, ... 'MetricsWarmupPeriod',1000,'MetricsWindowSize',500, ... 'Metrics',{'epsiloninsensitive' 'mse' maemetric})
Mdl =
incrementalRegressionLinear
IsWarm: 0
Metrics: [3×2 table]
ResponseTransform: 'none'
Beta: [0×1 double]
Bias: 0
Learner: 'svm'
Properties, Methods
Mdl is an incrementalRegressionLinear model object configured for incremental learning without an estimation period.
Fit the incremental model to the data by using the updateMetricsAndFit function. At each iteration:
Simulate a data stream by processing a chunk of 50 observations. Note that the chunk size is different from SGD batch size.
Overwrite the previous incremental model with a new one fitted to the incoming observations.
Store the estimated coefficient , the cumulative metrics, and the window metrics to see how they evolve during incremental learning.
% Preallocation numObsPerChunk = 50; nchunk = floor(n/numObsPerChunk); ei = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]); mse = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]); mae = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]); beta10 = zeros(nchunk+1,1); % Incremental fitting rng("default"); % For reproducibility for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); idx = ibegin:iend; Mdl = updateMetricsAndFit(Mdl,Xtrain(idx,:),ytrain(idx)); ei{j,:} = Mdl.Metrics{"EpsilonInsensitiveLoss",:}; mse{j,:} = Mdl.Metrics{"MeanSquaredError",:}; mae{j,:} = Mdl.Metrics{"MeanAbsoluteError",:}; beta10(j + 1) = Mdl.Beta(10); end
Mdl is an incrementalRegressionLinear model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetricsAndFit checks the performance of the model on the incoming observations, and then fits the model to those observations.
To see how the performance metrics and evolve during training, plot them on separate tiles.
tiledlayout(2,2) nexttile plot(beta10) ylabel('\beta_{10}') xlim([0 nchunk]) xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'g-.') xlabel('Iteration') nexttile h = plot(ei.Variables); xlim([0 nchunk]) ylabel('Epsilon Insensitive Loss') xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'g-.') legend(h,ei.Properties.VariableNames) xlabel('Iteration') nexttile h = plot(mse.Variables); xlim([0 nchunk]) ylabel('MSE') xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'g-.') legend(h,mse.Properties.VariableNames) xlabel('Iteration') nexttile h = plot(mae.Variables); xlim([0 nchunk]) ylabel('MAE') xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'g-.') legend(h,mae.Properties.VariableNames) xlabel('Iteration')
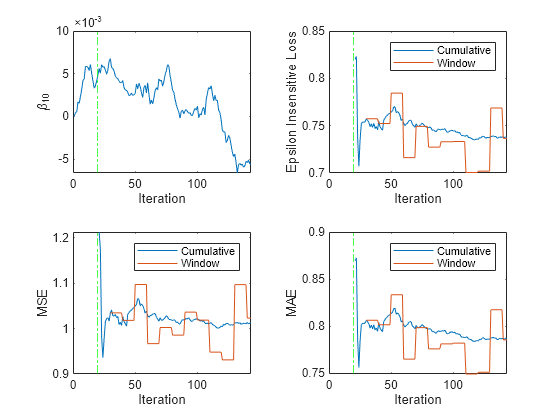
The plot suggests that updateMetricsAndFit does the following:
Fit during all incremental learning iterations.
Compute the performance metrics after the metrics warm-up period only.
Compute the cumulative metrics during each iteration.
Compute the window metrics after processing 500 observations (10 iterations).
Train a linear regression model by using fitrlinear, convert it to an incremental learner, track its performance, and fit it to streaming data. Carry over training options from traditional to incremental learning.
Load and Preprocess Data
Load the 2015 NYC housing data set, and shuffle the data. For more details on the data, see NYC Open Data.
load NYCHousing2015 rng(1); % For reproducibility n = size(NYCHousing2015,1); idxshuff = randsample(n,n); NYCHousing2015 = NYCHousing2015(idxshuff,:);
Suppose that the data collected from Manhattan (BOROUGH = 1) was collected using a new method that doubles its quality. Create a weight variable that attributes 2 to observations collected from Manhattan, and 1 to all other observations.
NYCHousing2015.W = ones(n,1) + (NYCHousing2015.BOROUGH == 1);
Extract the response variable SALEPRICE from the table. For numerical stability, scale SALEPRICE by 1e6.
Y = NYCHousing2015.SALEPRICE/1e6; NYCHousing2015.SALEPRICE = [];
Create dummy variable matrices from the categorical predictors.
catvars = ["BOROUGH" "BUILDINGCLASSCATEGORY" "NEIGHBORHOOD"]; dumvarstbl = varfun(@(x)dummyvar(categorical(x)),NYCHousing2015, ... 'InputVariables',catvars); dumvarmat = table2array(dumvarstbl); NYCHousing2015(:,catvars) = [];
Treat all other numeric variables in the table as linear predictors of sales price. Concatenate the matrix of dummy variables to the rest of the predictor data. Transpose the resulting predictor matrix.
idxnum = varfun(@isnumeric,NYCHousing2015,'OutputFormat','uniform'); X = [dumvarmat NYCHousing2015{:,idxnum}]';
Train Linear Regression Model
Fit a linear regression model to a random sample of half the data.
idxtt = randsample([true false],n,true); TTMdl = fitrlinear(X(:,idxtt),Y(idxtt),'ObservationsIn','columns', ... 'Weights',NYCHousing2015.W(idxtt))
TTMdl =
RegressionLinear
ResponseName: 'Y'
ResponseTransform: 'none'
Beta: [313×1 double]
Bias: 0.1116
Lambda: 2.1977e-05
Learner: 'svm'
Properties, Methods
TTMdl is a RegressionLinear model object representing a traditionally trained linear regression model.
Convert Trained Model
Convert the traditionally trained linear regression model to a linear regression model for incremental learning.
IncrementalMdl = incrementalLearner(TTMdl)
IncrementalMdl =
incrementalRegressionLinear
IsWarm: 1
Metrics: [1×2 table]
ResponseTransform: 'none'
Beta: [313×1 double]
Bias: 0.1116
Learner: 'svm'
Properties, Methods
Separately Track Performance Metrics and Fit Model
Perform incremental learning on the rest of the data by using the updateMetrics and fit functions. Simulate a data stream by processing 500 observations at a time. At each iteration:
Call
updateMetricsto update the cumulative and window epsilon insensitive loss of the model given the incoming chunk of observations. Overwrite the previous incremental model to update the losses in theMetricsproperty. Note that the function does not fit the model to the chunk of data—the chunk is "new" data for the model. Specify that the observations are oriented in columns, and specify the observation weights.Call
fitto fit the model to the incoming chunk of observations. Overwrite the previous incremental model to update the model parameters. Specify that the observations are oriented in columns, and specify the observation weights.Store the losses and last estimated coefficient .
% Preallocation idxil = ~idxtt; nil = sum(idxil); numObsPerChunk = 500; nchunk = floor(nil/numObsPerChunk); ei = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]); beta313 = [IncrementalMdl.Beta(end); zeros(nchunk,1)]; Xil = X(:,idxil); Yil = Y(idxil); Wil = NYCHousing2015.W(idxil); % Incremental fitting for j = 1:nchunk ibegin = min(nil,numObsPerChunk*(j-1) + 1); iend = min(nil,numObsPerChunk*j); idx = ibegin:iend; IncrementalMdl = updateMetrics(IncrementalMdl,Xil(:,idx),Yil(idx), ... 'ObservationsIn','columns','Weights',Wil(idx)); ei{j,:} = IncrementalMdl.Metrics{"EpsilonInsensitiveLoss",:}; IncrementalMdl = fit(IncrementalMdl,Xil(:,idx),Yil(idx),'ObservationsIn','columns', ... 'Weights',Wil(idx)); beta313(j + 1) = IncrementalMdl.Beta(end); end
IncrementalMdl is an incrementalRegressionLinear model object trained on all the data in the stream.
Alternatively, you can use updateMetricsAndFit to update performance metrics of the model given a new chunk of data, and then fit the model to the data.
Plot a trace plot of the performance metrics and estimated coefficient .
t = tiledlayout(2,1); nexttile h = plot(ei.Variables); xlim([0 nchunk]) ylabel('Epsilon Insensitive Loss') legend(h,ei.Properties.VariableNames) nexttile plot(beta313) ylabel('\beta_{313}') xlim([0 nchunk]) xlabel(t,'Iteration')

The cumulative loss gradually changes with each iteration (chunk of 500 observations), whereas the window loss jumps. Because the metrics window is 200 by default, updateMetrics measures the performance based on the latest 200 observations in each 500 observation chunk.
changes abruptly, then levels off as fit processes chunks of observations.
More About
Incremental learning, or online learning, is a branch of machine learning concerned with processing incoming data from a data stream, possibly given little to no knowledge of the distribution of the predictor variables, aspects of the prediction or objective function (including tuning parameter values), or whether the observations are labeled. Incremental learning differs from traditional machine learning, where enough labeled data is available to fit to a model, perform cross-validation to tune hyperparameters, and infer the predictor distribution.
Given incoming observations, an incremental learning model processes data in any of the following ways, but usually in this order:
Predict labels.
Measure the predictive performance.
Check for structural breaks or drift in the model.
Fit the model to the incoming observations.
For more details, see Incremental Learning Overview.
The adaptive scale-invariant solver for incremental learning, introduced in [1], is a gradient-descent-based objective solver for training linear predictive models. The solver is hyperparameter free, insensitive to differences in predictor variable scales, and does not require prior knowledge of the distribution of the predictor variables. These characteristics make it well suited to incremental learning.
The standard SGD and ASGD solvers are sensitive to differing scales among the predictor variables, resulting in models that can perform poorly. To achieve better accuracy using SGD and ASGD, you can standardize the predictor data, and tune the regularization and learning rate parameters. For traditional machine learning, enough data is available to enable hyperparameter tuning by cross-validation and predictor standardization. However, for incremental learning, enough data might not be available (for example, observations might be available only one at a time) and the distribution of the predictors might be unknown. These characteristics make parameter tuning and predictor standardization difficult or impossible to do during incremental learning.
The incremental fitting functions for regression fit and updateMetricsAndFit use the more conservative ScInOL1 version of the algorithm.
Tips
After creating a model, you can generate C/C++ code that performs incremental learning on a data stream. Generating C/C++ code requires MATLAB Coder™. For details, see Introduction to Code Generation.
Algorithms
During the estimation period, the incremental fitting functions fit and updateMetricsAndFit use the
first incoming EstimationPeriod observations
to estimate (tune) hyperparameters required for incremental training. Estimation occurs only
when EstimationPeriod is positive. This table describes the
hyperparameters and when they are estimated, or tuned.
| Hyperparameter | Model Property | Usage | Conditions |
|---|---|---|---|
| Predictor means and standard deviations |
| Standardize predictor data | The hyperparameters are estimated when both of these conditions apply:
|
| Learning rate | LearnRate
| Adjust the solver step size | The hyperparameter is estimated when both of these conditions apply:
|
| Half the width of the epsilon insensitive band | Epsilon
| Control the number of support vectors | The hyperparameter is estimated when both of these conditions apply:
|
During the estimation period, fit does not fit the model, and updateMetricsAndFit does not fit the model or update the performance metrics. At the end of the estimation period, the functions update the properties that store the hyperparameters.
If incremental learning functions are configured to standardize predictor variables, they do so using the means and standard deviations stored in the Mu and Sigma properties of the incremental learning model Mdl.
When you set
'Standardize',trueand a positive estimation period (seeEstimationPeriod), andMdl.MuandMdl.Sigmaare empty, incremental fitting functions estimate means and standard deviations using the estimation period observations.When you set
'Standardize','auto'(the default), the following conditions apply.If you create
incrementalRegressionLinearby converting a traditionally trained SVM regression model (CompactRegressionSVMorRegressionSVM), and theMuandSigmaproperties of the model being converted are empty arrays[], incremental learning functions do not standardize predictor variables. If theMuandSigmaproperties of the model being converted are nonempty, incremental learning functions standardize the predictor variables using the specified means and standard deviations. Incremental fitting functions do not estimate new means and standard deviations regardless of the length of the estimation period.If you create
incrementalRegressionLinearby converting a linear regression model (RegressionLinear), incremental learning functions does not standardize the data regardless of the length of the estimation period.If you do not convert a traditionally trained model, incremental learning functions standardize the predictor data only when you specify an SGD solver (see
Solver) and a positive estimation period (seeEstimationPeriod).
When incremental fitting functions estimate predictor means and standard deviations, the functions compute weighted means and weighted standard deviations using the estimation period observations. Specifically, the functions standardize predictor j (xj) using
xj is predictor j, and xjk is observation k of predictor j in the estimation period.
wj is observation weight j.
The
updateMetricsandupdateMetricsAndFitfunctions track model performance metrics ('Metrics') from new data when the incremental model is warm (IsWarm property). An incremental model becomes warm afterfitorupdateMetricsAndFitfit the incremental model to MetricsWarmupPeriod observations, which is the metrics warm-up period.If EstimationPeriod > 0, the functions estimate hyperparameters before fitting the model to data. Therefore, the functions must process an additional
EstimationPeriodobservations before the model starts the metrics warm-up period.The
Metricsproperty of the incremental model stores two forms of each performance metric as variables (columns) of a table,CumulativeandWindow, with individual metrics in rows. When the incremental model is warm,updateMetricsandupdateMetricsAndFitupdate the metrics at the following frequencies:Cumulative— The functions compute cumulative metrics since the start of model performance tracking. The functions update metrics every time you call the functions and base the calculation on the entire supplied data set.Window— The functions compute metrics based on all observations within a window determined by the MetricsWindowSize name-value pair argument.MetricsWindowSizealso determines the frequency at which the software updatesWindowmetrics. For example, ifMetricsWindowSizeis 20, the functions compute metrics based on the last 20 observations in the supplied data (X((end – 20 + 1):end,:)andY((end – 20 + 1):end)).Incremental functions that track performance metrics within a window use the following process:
Store a buffer of length
MetricsWindowSizefor each specified metric, and store a buffer of observation weights.Populate elements of the metrics buffer with the model performance based on batches of incoming observations, and store corresponding observation weights in the weights buffer.
When the buffer is filled, overwrite
Mdl.Metrics.Windowwith the weighted average performance in the metrics window. If the buffer is overfilled when the function processes a batch of observations, the latest incomingMetricsWindowSizeobservations enter the buffer, and the earliest observations are removed from the buffer. For example, supposeMetricsWindowSizeis 20, the metrics buffer has 10 values from a previously processed batch, and 15 values are incoming. To compose the length 20 window, the functions use the measurements from the 15 incoming observations and the latest 5 measurements from the previous batch.
The software omits an observation with a
NaNprediction when computing theCumulativeandWindowperformance metric values.
References
[1] Kempka, Michał, Wojciech Kotłowski, and Manfred K. Warmuth. "Adaptive Scale-Invariant Online Algorithms for Learning Linear Models." Preprint, submitted February 10, 2019. https://arxiv.org/abs/1902.07528.
[2] Langford, J., L. Li, and T. Zhang. “Sparse Online Learning Via Truncated Gradient.” J. Mach. Learn. Res., Vol. 10, 2009, pp. 777–801.
[3] Shalev-Shwartz, S., Y. Singer, and N. Srebro. “Pegasos: Primal Estimated Sub-Gradient Solver for SVM.” Proceedings of the 24th International Conference on Machine Learning, ICML ’07, 2007, pp. 807–814.
[4] Xu, Wei. “Towards Optimal One Pass Large Scale Learning with Averaged Stochastic Gradient Descent.” CoRR, abs/1107.2490, 2011.
Extended Capabilities
Usage notes and limitations:
All object functions of an
incrementalRegressionLinearmodel object support code generation.If you configure
Mdlto shuffle data (see Solver and Shuffle), thefitfunction randomly shuffles each incoming batch of observations before it fits the model to the batch. The order of the shuffled observations might not match the order generated by MATLAB.When you generate code that loads or creates an
incrementalRegressionLinearmodel object, theNumPredictorsproperty must reflect the number of predictor variables.
For more information, see Introduction to Code Generation.
Version History
Introduced in R2020b
See Also
Functions
fit|updateMetrics|updateMetricsAndFit|predict|incrementalLearner (RegressionLinear)|incrementalLearner (RegressionSVM)
Objects
Topics
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)