plotInteraction
Plot interaction effects of two predictors in linear regression model
Syntax
Description
plotInteraction(
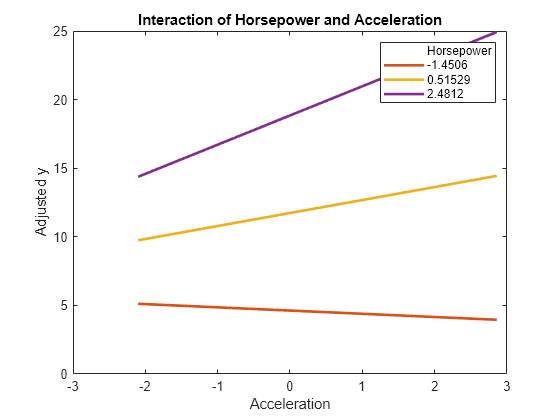
creates a plot of the main effects of the
two selected predictors mdl,var1,var2)var1 and var2 and
their conditional effects
in the linear regression model mdl. Horizontal lines through
the effect values indicate their 95% confidence intervals.
plotInteraction(
specifies the plot type mdl,var1,var2,ptype)ptype. For example, if
ptype is 'predictions', then
plotInteraction plots the adjusted response function as a
function of the second predictor, with the first predictor fixed at specific values.
For details, see Conditional Effect.
h = plotInteraction(___)h. Use h
to modify the properties of a specific line after you create the plot. For a list of
properties, see Line Properties.
Examples
Input Arguments
Output Arguments
More About
Tips
The data cursor displays the values of the selected plot point in a data tip (small text box located next to the data point). The data tip includes the x-axis and y-axis values for the selected point, along with the observation name or number.
Alternative Functionality
A
LinearModelobject provides multiple plotting functions.When creating a model, use
plotAddedto understand the effect of adding or removing a predictor variable.When verifying a model, use
plotDiagnosticsto find questionable data and to understand the effect of each observation. Also, useplotResidualsto analyze the residuals of the model.After fitting a model, use
plotAdjustedResponse,plotPartialDependence, andplotEffectsto understand the effect of a particular predictor. UseplotInteractionto understand the interaction effect between two predictors. Also, useplotSliceto plot slices through the prediction surface.