mvnrnd

Números aleatorios normales multivariantes

Sintaxis

R = mvnrnd(mu,Sigma,n)

R = mvnrnd(mu,Sigma)

Descripción

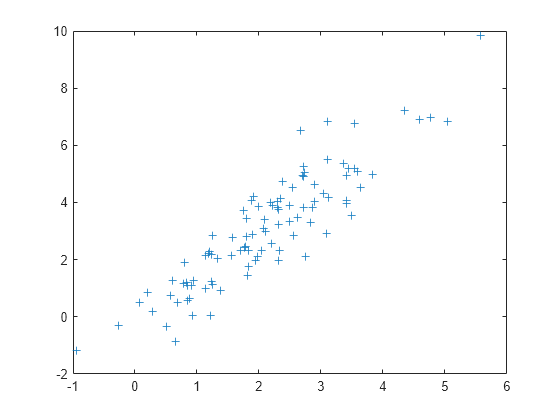
R = mvnrnd(mu,Sigma,n) devuelve una matriz R de n vectores aleatorios seleccionados de la misma distribución normal multivariante, con el vector de media mu y la matriz de covarianzas Sigma. Para obtener más información, consulte Distribución normal multivariante.

R = mvnrnd(mu,Sigma) devuelve una matriz de m por d R de vectores aleatorios obtenidos de m distribuciones independientes normales multivariantes de d dimensiones, con las medias y covarianzas especificadas por mu y Sigma, respectivamente. Cada fila de R es un solo vector aleatorio normal multivariante.

Ejemplos

Generar números aleatorios normales multivariantes

Genere números aleatorios a partir de la misma distribución normal multivariante.

Defina mu y Sigma y genere 100 números aleatorios.

mu = [2 3];
Sigma = [1 1.5; 1.5 3];
rng('default')  % For reproducibility
R = mvnrnd(mu,Sigma,100);

Represente los números aleatorios.

plot(R(:,1),R(:,2),'+')

Muestra de diferentes distribuciones normales multivariantes

Obtenga una muestra de forma aleatoria de 5 distribuciones normales tridimensionales diferentes.

Indique las medias mu y las covarianzas Sigma de las distribuciones. Deje que todas las distribuciones compartan la misma matriz de covarianzas, pero varíe los vectores de media.

firstDim = (1:5)';
mu = repmat(firstDim,1,3)

mu = 5×3

     1     1     1
     2     2     2
     3     3     3
     4     4     4
     5     5     5

Sigma = eye(3)

Sigma = 3×3

     1     0     0
     0     1     0
     0     0     1

Obtenga una muestra aleatoriamente de cada una de las cinco distribuciones.

rng('default')  % For reproducibility
R = mvnrnd(mu,Sigma)

R = 5×3

    1.5377   -0.3077   -0.3499
    3.8339    1.5664    5.0349
    0.7412    3.3426    3.7254
    4.8622    7.5784    3.9369
    5.3188    7.7694    5.7147

Represente los resultados.

scatter3(R(:,1),R(:,2),R(:,3))

Argumentos de entrada

mu — Medias de las distribuciones normales multivariantes

vector numérico | matriz numérica

Medias de las distribuciones normales multivariantes, especificadas como un vector numérico de 1 por d o una matriz numérica de m por d.

• Si mu es un vector, entonces mvnrnd replica el vector para coincidir con las siguiente dimensión de Sigma.

• Si mu es una matriz, cada fila de mu es el vector medio de una sola distribución normal multivariante.

Tipos de datos: single | double

Sigma — Covarianzas de las distribuciones normales multivariantes

matriz semidefinida, positiva y simétrica | arreglo numérico

Las covarianzas de las distribuciones normales multivariantes, especificadas como una matriz semidefinida, positiva y simétrica de d por d o un arreglo numérico de d por d por m.

• Si Sigma es una matriz, mvnrnd replicará la matriz para coincidir con el número de filas de mu.

• Si Sigma es un arreglo, cada página de Sigma, Sigma(:,:,i), corresponderá a la matriz de covarianzas de una sola distribución normal multivariante y, por tanto, se tratará de una matriz semidefinida, positiva y simétrica.

Si las matrices de covarianzas son diagonales, que contienen varianzas en la diagonal sin covarianzas fuera de ellas, también puede especificar Sigma como un vector de 1 por d o un arreglo de 1 por d por m que contenga solo las entradas diagonales.

Tipos de datos: single | double

n — Cantidad de números aleatorios multivariantes

entero escalar positivo

Cantidad de números aleatorios multivariantes, especificada como un entero escalar positivo. n especifica el número de filas de R.

Tipos de datos: single | double

Argumentos de salida

R — Números aleatorios normales multivariantes

matriz numérica

Números aleatorios normales multivariantes, devueltos de una de las siguientes formas:

• Matriz numérica de m por d, donde m y d son las dimensiones especificadas por mu y Sigma

• Matriz numérica de n por d, donde n es el argumento de entrada especificado y d es la dimensión especificada por mu y Sigma

Si mu es una matriz y Sigma es un arreglo, mvnrnd calculará R(i,:) usando mu(i,:) y Sigma(:,:,i).

Más acerca de

Distribución normal multivariante

La distribución normal multivariante es una generalización de la distribución normal univariante a dos o más variables. Tiene dos parámetros, un vector de media μ y una matriz de covarianzas Σ, que son análogos de los parámetros de media y varianza de una distribución normal univariante. Los elementos de la diagonal de Σ contienen las varianzas de cada variable, y los elementos fuera de la diagonal de Σ contienen las covarianzas entre variables.

La función de densidad de probabilidad (pdf) de la distribución normal multivariante dimensional d es

$$y\text{ = }f(x,\mu ,\Sigma )\text{ = }\frac{\text{1}}{\sqrt{\left|\Sigma \right|{\text{(2}\pi \text{)}}^d}}\exp \left(-\frac{\text{1}}{\text{2}}\text{(}x\text{-}\mu \text{) }{\Sigma }^{\text{-1}}\text{(}x\text{-}\mu \text{)'}\right)$$

donde x y μ son vectores de 1 por d y Σ es una matriz definida positiva y simétrica de d por d. Solo mvnrnd admite matrices semidefinidas positivas Σ, que pueden ser singulares. La pdf no puede tener la misma forma cuando Σ es singular.

La función de distribución acumulativa (cdf) multivariante evaluada en x es la probabilidad de que un vector aleatorio v, distribuido como una normal multivariante, se encuentre dentro del rectángulo semiinfinito con límites superiores definido por x:

$$\mathrm{Pr}\{v(1)\le x(1),v(2)\le x(2),\mathrm{...},v(d)\le x(d)\}.$$

Aunque la cdf normal multivariante no tiene una forma cerrada, mvncdf puede calcular los valores de cdf de manera numérica.

Sugerencias

• mvnrnd requiere que la matriz Sigma sea simétrica. Si Sigma tiene una pequeña asimetría, puede usar (Sigma + Sigma')/2 en su lugar para solucionarla.

• En el caso de una sola dimensión, Sigma es la varianza, no la desviación estándar. Por ejemplo, mvnrnd(0,4) es igual a normrnd(0,2), donde 4 es la varianza y 2 es la desviación estándar.

Referencias

[1] Kotz, S., N. Balakrishnan, and N. L. Johnson. Continuous Multivariate Distributions: Volume 1: Models and Applications. 2nd ed. New York: John Wiley & Sons, Inc., 2000.

Capacidades ampliadas

Arreglos GPU

Acelere código mediante la ejecución en una unidad de procesamiento gráfico (GPU) mediante Parallel Computing Toolbox™.

Esta función es totalmente compatible con los arreglos de GPU. Para obtener más información, consulte Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Historial de versiones

Introducido antes de R2006a

Consulte también

mvnpdf | mvncdf | normrnd

Temas

• Distribución normal multivariante

×

Abrir ejemplo

Tiene una versión modificada de este ejemplo. ¿Desea abrir este ejemplo con sus modificaciones?

No, sobrescribir la versión modificada Sí