La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

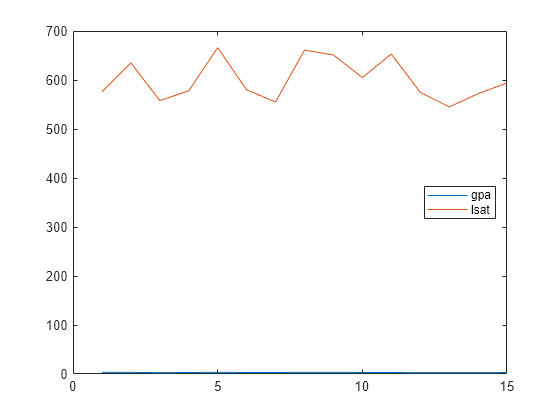
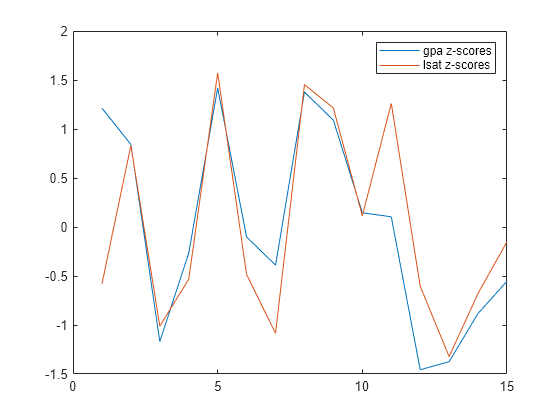
zscore

Puntuaciones z estandarizadas

Sintaxis

Z = zscore(X)

Z = zscore(X,flag)

Z = zscore(X,flag,'all')

Z = zscore(X,flag,dim)

Z = zscore(X,flag,vecdim)

[Z,mu,sigma] = zscore(___)

Descripción

Z = zscore(X) devuelve la puntuación z para cada elemento de X de manera tal que las columnas de X están centradas para obtener una media de 0 y escaladas para obtener una desviación estándar de 1. Z tiene el mismo tamaño que X.

• Si X es un vector, Z es un vector de puntuaciones z.

• Si X es una matriz, Z es una matriz del mismo tamaño que X, y cada columna de Z tiene una media de 0 y una desviación estándar de 1.

• En los arreglos multidimensionales, las puntuaciones z de Z se calculan a lo largo de la primera dimensión no singular de X.

Z = zscore(X,flag) escala X usando la desviación estándar indicada por flag.

• Si flag es 0 (valor predeterminado), zscore escala X usando la desviación estándar de la muestra, con n - 1 en el denominador de la fórmula de la desviación estándar. zscore(X,0) es igual que zscore(X).

• Si flag es 1, zscore escala X usando la desviación estándar de la población, con n en el denominador de la fórmula de la desviación estándar.

Z = zscore(X,flag,'all') estandariza X usando la media y la desviación estándar de todos los valores de X.

Z = zscore(X,flag,dim) estandariza X a lo largo de la dimensión operativa dim. Por ejemplo, para una matriz X, si dim = 1, zscore usa las medias y las desviaciones estándar a lo largo de las columnas de X; si dim = 2, zscore usa las medias y las desviaciones estándar a lo largo de las filas de X.

Z = zscore(X,flag,vecdim) estandariza X sobre las dimensiones especificadas por el vector vecdim. Por ejemplo, si X es una matriz, zscore(X,0,[1 2]) equivale a zscore(X,0,'all') porque cada elemento de una matriz está dentro de la parte del arreglo definida por las dimensiones 1 y 2.

[Z,mu,sigma] = zscore(___) también devuelve las medias y las desviaciones estándar usadas para centrar y escalar, mu y sigma, respectivamente. Puede utilizar cualquiera de los argumentos de entrada de las sintaxis anteriores.

Ejemplos

Puntuaciones z de dos vectores de datos

Calcule y represente las puntuaciones $$z$$ de dos vectores de datos y compare los resultados.

Cargue los datos de muestra.

load lawdata

En el espacio de trabajo se cargan dos variables: gpa y lsat.

Represente ambas variables en los mismos ejes.

plot([gpa,lsat])
legend('gpa','lsat','Location','East')

Es difícil comparar estas dos medidas porque están en una escala muy diferente.

Represente las puntuaciones $$z$$ de gpa y lsat en los mismos ejes.

Zgpa = zscore(gpa);
Zlsat = zscore(lsat);
plot([Zgpa, Zlsat])
legend('gpa z-scores','lsat z-scores','Location','Northeast')

Ahora, puede ver el rendimiento relativo de los individuos con respecto a sus resultados de gpa y lsat. Por ejemplo, los resultados gpa y lsat del tercer individuo son ambos una desviación estándar por debajo de la media de la muestra. El gpa del undécimo individuo está alrededor de la media de la muestra, pero tiene una puntuación lsat de casi 1,25 desviaciones estándar por encima de la media de la muestra.

Compruebe la media y la desviación estándar de las puntuaciones $$z$$ que ha creado.

 mean([Zgpa,Zlsat])

ans = 1×2
10-14 ×

   -0.1088    0.0357

 std([Zgpa,Zlsat])

ans = 1×2

     1     1

Por definición, las puntuaciones $$z$$ de gpa y lsat tienen una media de 0 y una desviación estándar de 1.

Puntuaciones z de una población en comparación con una muestra

Cargue los datos de muestra.

load lawdata

En el espacio de trabajo se cargan dos variables: gpa y lsat.

Calcule las puntuaciones $$z$$ de gpa usando la fórmula de la población para la desviación estándar.

Z1 = zscore(gpa,1); % population formula
Z0 = zscore(gpa,0); % sample formula
disp([Z1 Z0])

    1.2554    1.2128
    0.8728    0.8432
   -1.2100   -1.1690
   -0.2749   -0.2656
    1.4679    1.4181
   -0.1049   -0.1013
   -0.4024   -0.3888
    1.4254    1.3771
    1.1279    1.0896
    0.1502    0.1451
    0.1077    0.1040
   -1.5076   -1.4565
   -1.4226   -1.3743
   -0.9125   -0.8815
   -0.5724   -0.5530

Para una muestra de una población, la fórmula de desviación estándar de la población con $$n$$ en el denominador corresponde a la estimación de máxima verosimilitud de la desviación estándar de la población y podría estar sesgada. La fórmula de la desviación estándar de la muestra, por otro lado, es el estimador no sesgado de la desviación estándar de la población para una muestra.

Puntuaciones z de una matriz de datos

Calcule las puntuaciones $$z$$ usando la media y la desviación estándar calculadas a lo largo de las columnas o filas de una matriz de datos.

Cargue los datos de muestra.

load flu

El arreglo del conjunto de datos flu se carga en el espacio de trabajo. flu tiene 52 observaciones sobre 11 variables. La primera variable contiene fechas (en semanas). Las otras variables contienen estimaciones sobre la gripe para diferentes regiones de Estados Unidos.

Convierta el arreglo del conjunto de datos en una matriz de datos.

flu2 = double(flu(:,2:end));

La nueva matriz de datos, flu2, es una matriz de datos doble de 52 por 10. Las filas corresponden a las semanas y las columnas corresponden a las regiones de Estados Unidos en el arreglo del conjunto de datos flu.

Estandarice la estimación sobre la gripe para cada región (las columnas de flu2).

Z1 = zscore(flu2,[ ],1);

Puede ver las puntuaciones $$z$$ en el editor de variables haciendo doble clic en la matriz Z1 creada en el espacio de trabajo.

Estandarice la estimación sobre la gripe para cada semana (las filas de flu2).

Z2 = zscore(flu2,[ ],2);

Puntuaciones z de un arreglo multidimensional

Encuentre las puntuaciones z de un arreglo multidimensional especificando estandarizar los datos a lo largo de diferentes dimensiones. Compare los resultados al usar los argumentos de entrada 'all', dim y vecdim.

Cree un arreglo de 3 por 4 por 2.

X = reshape(1:24,[3 4 2])

X = 
X(:,:,1) =

     1     4     7    10
     2     5     8    11
     3     6     9    12


X(:,:,2) =

    13    16    19    22
    14    17    20    23
    15    18    21    24

Estandarice X usando la media y la desviación estándar de todos los valores de X.

Zall = zscore(X,0,'all')

Zall = 
Zall(:,:,1) =

   -1.6263   -1.2021   -0.7778   -0.3536
   -1.4849   -1.0607   -0.6364   -0.2121
   -1.3435   -0.9192   -0.4950   -0.0707


Zall(:,:,2) =

    0.0707    0.4950    0.9192    1.3435
    0.2121    0.6364    1.0607    1.4849
    0.3536    0.7778    1.2021    1.6263

El arreglo multidimensional resultante de las puntuaciones z tiene una media de 0 y una desviación estándar de 1. Por ejemplo, calcule la media y la desviación estándar de Zall.

mZall = mean(Zall(:,:,:),'all')

mZall = -9.2519e-18

sZall = std(Zall(:,:,:),0,'all')

sZall = 1.0000

Ahora estandarice X a lo largo de la segunda dimensión.

Zdim = zscore(X,0,2)

Zdim = 
Zdim(:,:,1) =

   -1.1619   -0.3873    0.3873    1.1619
   -1.1619   -0.3873    0.3873    1.1619
   -1.1619   -0.3873    0.3873    1.1619


Zdim(:,:,2) =

   -1.1619   -0.3873    0.3873    1.1619
   -1.1619   -0.3873    0.3873    1.1619
   -1.1619   -0.3873    0.3873    1.1619

Los elementos en cada fila de cada página de Zdim tienen una media de 0 y una desviación estándar de 1. Por ejemplo, calcule la media y la desviación estándar de la primera fila de la segunda página de Zdim.

mZdim = mean(Zdim(1,:,2),'all')

mZdim = 0

sZdim = std(Zdim(1,:,2),0,'all')

sZdim = 1

Finalmente, estandarice X en función de la segunda y la tercera dimensión.

Zvecdim = zscore(X,0,[2 3])

Zvecdim = 
Zvecdim(:,:,1) =

   -1.4289   -1.0206   -0.6124   -0.2041
   -1.4289   -1.0206   -0.6124   -0.2041
   -1.4289   -1.0206   -0.6124   -0.2041


Zvecdim(:,:,2) =

    0.2041    0.6124    1.0206    1.4289
    0.2041    0.6124    1.0206    1.4289
    0.2041    0.6124    1.0206    1.4289

Los elementos en cada porción de Zvecdim(i,:,:) tienen una media de 0 y una desviación estándar de 1. Por ejemplo, calcule la media y la desviación estándar de los elementos de Zvecdim(1,:,:).

mZvecdim = mean(Zvecdim(1,:,:),'all')

mZvecdim = 2.7756e-17

sZvecdim = std(Zvecdim(1,:,:),0,'all')

sZvecdim = 1

Puntuaciones z, media y desviación estándar

Devuelva la media y la desviación estándar usadas para calcular las puntuaciones $$z$$.

Cargue los datos de muestra.

load lawdata

En el espacio de trabajo se cargan dos variables: gpa y lsat.

Devuelva las puntuaciones $$z$$, la media y la desviación estándar de gpa.

[Z,gpamean,gpastdev] = zscore(gpa)

Z = 15×1

    1.2128
    0.8432
   -1.1690
   -0.2656
    1.4181
   -0.1013
   -0.3888
    1.3771
    1.0896
    0.1451
      ⋮

gpamean = 3.0947

gpastdev = 0.2435

Argumentos de entrada

X — Datos de entrada

vector | matriz | arreglo multidimensional

Datos de entrada, especificados como un vector, una matriz o un arreglo multidimensional.

Tipos de datos: double | single

flag — Indicador de la desviación estándar

0 (predeterminado) | 1

Indicador de la desviación estándar usado para calcular las puntuaciones z, especificado como 0 o 1.

• Si flag es 0 (valor predeterminado), zscore escala X usando la desviación estándar de la muestra. zscore(X,0) es igual que zscore(X).

• Si flag es 1, zscore escala X usando la desviación estándar de la población.

dim — Dimensión

escalar entero positivo

Dimensión a lo largo de la que calcular las puntuaciones z de X, especificada como un escalar entero positivo. Si no especifica un valor, el valor predeterminado es la primera dimensión del arreglo cuyo tamaño no sea igual a 1.

Por ejemplo, para una matriz X, si dim = 1, zscore usa las medias y las desviaciones estándar a lo largo de las columnas de X, y si dim = 2, zscore usa las medias y las desviaciones estándar a lo largo de las filas de X.

vecdim — Vector de dimensiones

vector entero positivo

Vector de dimensiones a lo largo del que calcular las puntuaciones z de X, especificado como un vector entero positivo. Cada elemento de vecdim representa una dimensión del arreglo de entrada X. La salida Z tiene las mismas dimensiones que X, pero la media mu y la desviación estándar sigma tienen una longitud de 1 en las dimensiones operativas. El resto de las longitudes de las dimensiones son iguales para X, mu y sigma.

Por ejemplo, si X es un arreglo de 2 por 3 por 3, zscore(X,0,[1 2]) usa las medias y las desviaciones estándar a lo largo de las páginas de X para estandarizar los valores de X.

Tipos de datos: single | double

Argumentos de salida

Z — Puntuaciones z-

vector | matriz | arreglo multidimensional

Puntuaciones z-, devueltas como un vector, una matriz o un arreglo multidimensional. Z tiene las mismas dimensiones que X.

Los valores de Z dependen de si especifica 'all', dim o vecdim. Si no especifica ninguno de estos argumentos de entrada, se aplican las siguientes condiciones:

• Si X es un vector, Z es un vector de puntuaciones z con una media de 0 y una varianza de 1.

• Si X es un arreglo, zscore estandariza a lo largo de la primera dimensión no singular de X.

Para ver un ejemplo que demuestre las diferencias en Z cuando usa 'all', dim y vecdim, consulte Puntuaciones z de un arreglo multidimensional.

mu — Media

escalar | vector | matriz | arreglo multidimensional

Media de X usada para calcular las puntuaciones z, devuelta como un escalar, un vector, una matriz o un arreglo multidimensional. mu tiene una longitud de 1 en las dimensiones operativas especificadas. El resto de las longitudes de las dimensiones son iguales para X e mu.

Por ejemplo, si X es un arreglo de 2 por 3 por 3 y vecdim es [1 2], mu es un arreglo de medias de 1 por 1 por 3. Cada valor de mu corresponde a la media de una página de X.

sigma — Desviación estándar

escalar | vector | matriz | arreglo multidimensional

Desviación estándar de X usada para calcular las puntuaciones z, devuelta como un escalar, un vector, una matriz o un arreglo multidimensional. sigma tiene una longitud de 1 en las dimensiones operativas especificadas. El resto de las longitudes de las dimensiones son iguales para X e sigma.

Por ejemplo, si X es un arreglo de 2 por 3 por 3 y vecdim es [1 2], sigma es un arreglo de desviaciones estándar de 1 por 1 por 3. Cada valor de sigma corresponde a la desviación estándar de una página de X.

Más acerca de

Puntuación z

Para una variable aleatoria X con una media μ y una desviación estándar σ, la puntuación z de un valor x es

$$z=\frac{\left(x-\mu \right)}{\sigma }.$$

. Para los datos de muestra con una media $$\overline{X}$$ y una desviación estándar S, la puntuación z de un punto de datos x es

$$z=\frac{\left(x-\overline{X}\right)}{S}.$$

.

Las puntuaciones z miden la distancia de un punto de datos desde la media en términos de la desviación estándar. Esto también se denomina estandarización de datos. El conjunto de datos estandarizados tiene una media de 0 y una desviación estándar de 1, y conserva las propiedades de forma del conjunto de datos original (misma asimetría y curtosis).

Puede usar las puntuaciones z para colocar los datos en la misma escala antes de realizar más análisis. Esto le permite comparar dos o más conjuntos de datos con diferentes unidades.

Arreglo multidimensional

Un arreglo multidimensional tiene más de dos dimensiones. Por ejemplo, si X es un arreglo de 1 por 3 por 4, X es un arreglo tridimensional.

Primera dimensión no singular

La primera dimensión no singular es la primera dimensión de un arreglo cuyo tamaño no es igual a 1. Por ejemplo, si X es un arreglo de 1 por 2 por 3 por 4, la segunda dimensión es la primera dimensión no singular de X.

Desviación estándar de muestra

La desviación estándar de la muestra S viene dada por

$$S=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left(x_i-\overline{X}\right)}^2}}{n-1}}.$$

S es la raíz cuadrada de un estimador no sesgado de la varianza de la población de la que se extrae X, siempre que X consista en muestras independientes distribuidas de forma idéntica. $$\overline{X}$$ es la media de la muestra.

Observe que el denominador en esta fórmula de varianza es n – 1.

Desviación estándar de la población

Si los datos son toda la población de valores, puede usar la desviación estándar de la población.

$$\sigma =\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left(x_i-\mu \right)}^2}}{n}}.$$

Si X es una muestra aleatoria de una población, la media μ es estimada por la media de la muestra, y σ es el estimador de máxima verosimilitud sesgado de la desviación estándar de la población.

Observe que el denominador en esta fórmula de varianza es n.

Algoritmos

zscore devuelve NaN para cualquier muestra que contenga NaN.

zscore devuelve 0 para cualquier muestra que sea constante (todos los valores son los mismos). Por ejemplo, si X es un vector del mismo valor numérico, Z es un vector de 0.

Capacidades ampliadas

Arreglos altos

Realice cálculos con arreglos que tienen más filas de las que caben en la memoria.

Esta función es totalmente compatible con arreglos altos. Para obtener más información, consulte Arreglos altos.

Generación de código C/C++

Genere código C y C++ mediante MATLAB® Coder™.

Notas y limitaciones de uso:

• Los argumentos de entrada 'all' y vecdim no son compatibles.

• El argumento de entrada dim debe ser una constante en tiempo de compilación.

• Si no especifica el argumento de entrada dim, la dimensión en funcionamiento (o en operación) puede ser diferente en el código generado. Como resultado, se podrían producir errores en el tiempo de ejecución. Para obtener más información, consulte .

Para obtener más información sobre la generación de código, consulte Introduction to Code Generation y General Code Generation Workflow.

Entorno basado en subprocesos

Ejecute código en segundo plano con MATLAB® backgroundPool o acelere código con Parallel Computing Toolbox™ ThreadPool.

Esta función es totalmente compatible con los entornos basados en procesos. Para obtener más información, consulte Ejecutar funciones de MATLAB en entornos basados en subprocesos.

Arreglos GPU

Acelere código mediante la ejecución en una unidad de procesamiento gráfico (GPU) mediante Parallel Computing Toolbox™.

Notas y limitaciones de uso:

• Los argumentos de entrada 'all' y vecdim no son compatibles.

Para obtener más información, consulte Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Historial de versiones

Introducido antes de R2006a

Consulte también

mean | std | normalize | rescale