odeMassMatrix
Description
An odeMassMatrix object represents the mass matrix for a system
of ordinary differential equations.
ode objects can represent problems of the form , where is a mass matrix that can be full or sparse. The mass matrix encodes linear
combinations of derivatives on the left side of the equation.
Create an ode object to
represent the ODE problem, and specify the odeMassMatrix object as the value
of the MassMatrix property to incorporate a mass matrix into the
problem.
Creation
Description
M = odeMassMatrixodeMassMatrix object with empty properties.
M = odeMassMatrix(PropertyName=Value)
Properties
Mass matrix, specified as a matrix or handle to a function that evaluates the mass matrix.
ode objects can represent problems of the form , where is a mass matrix that can be full or sparse. The mass matrix encodes
linear combinations of derivatives on the left side of the equation.
When the mass matrix is nonsingular, the equation simplifies to and the ODE has a solution for any initial value. However, it is often more convenient and natural to express the model in terms of the mass matrix directly using , and avoiding the computation of the matrix inverse reduces the storage and execution time needed to solve the problem.
When the mass matrix is singular, the problem is a system of differential algebraic equations (DAEs). A DAE has a solution only when the initial values are consistent; that is, you must specify the initial slope using the
InitialSlopeproperty of theodeobject such that the initial conditions are all consistent, . For more information, see Solve Differential Algebraic Equations (DAEs).
You can specify the value of the MassMatrix property as:
A constant matrix with calculated values for .
A handle to a function that computes the matrix elements and that accepts two input arguments,
M = Mass(t,y). To give the function access to parameter values in theParametersproperty, specify a third input argument in the function definition,M = Mass(t,y,p).
Example: M = odeMassMatrix(MassMatrix=@Mass) specifies the
function Mass that evaluates the mass matrix.
Example: M = odeMassMatrix(MassMatrix=[1 0; -2 1]) specifies a
constant mass matrix.
Data Types: single | double | function_handle
Complex Number Support: Yes
Singular mass matrix toggle, specified as "maybe",
"yes", or "no". The default value of
"maybe" causes the solver to test whether the problem is a
differential algebraic equation (DAE) by testing whether the mass matrix is singular.
Avoid this check by specifying "yes" if you know the system is a DAE
with a singular mass matrix, or "no" if it is not.
Example:
M = odeMassMatrix(MassMatrix=X,Singular="no")
State dependence of the mass matrix, specified as "weak",
"strong", or "none".
For ODE problems of the form , set the
StateDependenceproperty to"none". This value ensures that the solver calls the mass matrix function with a single argument as inMass(t)(or two arguments as inMass(t,p)if you use theParametersproperty of theodeobject to pass parameters).If the mass matrix depends on
y, then setStateDependenceto either"weak"(default) or"strong". In both cases, the solver calls the mass matrix function with two arguments as inMass(t,y)(or three arguments as inMass(t,y,p)if you use theParametersproperty of theodeobject to pass parameters). However, a value of"weak"results in implicit solvers using approximations when solving algebraic equations.
Example:
M = odeMassMatrix(MassMatrix=@Mass,StateDependence="none") specifies
that the mass matrix function Mass depends only on
t.
Mass matrix sparsity pattern, specified as a sparse matrix. Use this property to
specify the sparsity pattern of the matrix . The sparse matrix S has S(i,j) =
1 if, for any k, the (i,k) component
of depends on component j of y.
This property is similar to the MvPattern option of
odeset.
Note
The SparsityPattern property is used by the
ode15s, ode23t, and
ode23tb solvers when StateDependence is
"strong".
Example:
M =
odeMassMatrix(MassMatrix=@Mass,StateDependence="strong",SparsityPattern=S)
Data Types: single | double
Examples
Consider this system of first-order equations.
The left side of the equations contain time derivatives, . However, because the derivative for does not appear in the system, the equations define a system of differential algebraic equations. Rewriting the system in the form shows a constant, singular mass matrix on the left side.
Solve the system of equations using the initial values [1 1 -2] by creating an ode object to represent the problem.
Specify the initial values in the
InitialValueproperty.Specify the system of equations as an anonymous function in the
ODEFcnproperty.Use an
odeMassMatrixobject to specify the constant, singular mass matrix in theMassMatrixproperty.
F = ode;
F.InitialValue = [1 1 -2];
F.ODEFcn = @(t,y) [y(1)*y(3)-y(2);
y(1)-1;
y(1)+y(2)+y(3)];
F.MassMatrix = odeMassMatrix(MassMatrix=[1 0 0; 0 1 0; 0 0 0],Singular="yes");Display the ode object. The SelectedSolver property shows that the ode15s solver was automatically chosen for this problem.
F
F =
ode with properties:
Problem definition
ODEFcn: @(t,y)[y(1)*y(3)-y(2);y(1)-1;y(1)+y(2)+y(3)]
InitialTime: 0
InitialValue: [1 1 -2]
Jacobian: []
MassMatrix: [1×1 odeMassMatrix]
EquationType: standard
Solver properties
AbsoluteTolerance: 1.0000e-06
RelativeTolerance: 1.0000e-03
Solver: auto
SelectedSolver: ode15s
Show all properties
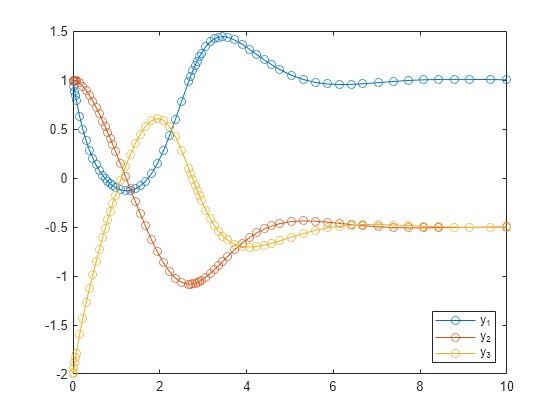
Solve the system of equations over the time interval [0 10] by using the solve method. Plot all three solution components.
S = solve(F,0,10); plot(S.Time,S.Solution,"-o") legend("y_1","y_2","y_3",Location="southeast")
Version History
Introduced in R2023bYou can specify the mass matrix MassMatrix and sparsity pattern
SparsityPattern as single-precision sparse matrices. You can also
specify MassMatrix as a function handle that returns single-precision
outputs.
See Also
ode | odeJacobian | odeEvent | ODEResults | odeset
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)