ode
Description
An ode object defines a system of ordinary differential equations
or differential algebraic equations to solve.
You can solve initial value problems of the form , , or problems that involve a mass matrix, .
Define aspects of the problem using properties of the ode object, such as
ODEFcn, InitialTime, and
InitialValue. You can select a specific solver to use, or let
MATLAB® choose an appropriate solver based on properties of the equations. After you
create an ode object, you can solve the equations using the
solve or solutionFcn object functions.
Creation
Description
F = odeode object
with default properties.
F = ode(PropertyName=Value)ODEFcn,
InitialTime, and InitialValue
properties.
Properties
Problem Definition
Equations to solve, specified as a function handle that defines the system of differential equations to be integrated. The function handle can be an anonymous function or a handle to a named function file.
The function
dydt = ODEFcn(t,y), for a scalartand a column vectory, must return a column vectordydtthat corresponds to .ODEFcnmust accept at least two input arguments,tandy, even if one of the arguments is not used in the function.The function
f = ODEFcn(t,y,yp), whenEquationTypeis"fullyimplicit"and for a scalartand column vectorsyandyp, must return a column vectorfthat corresponds to .ODEFcnmust accept at least three input arguments,t,y, andyp, even if one of the arguments is not used in the function. (since R2024b)The function
dydt = ODEFcn(t,y,Z), whenEquationTypeis"delay"and for a scalart, column vectory, and matrixZ, must return a column vectordydtthat corresponds to when the solver isdde23or , for delays d(j), when the solver isddesd.ODEFcnmust accept at least three input arguments,t,y, andZ, even if one of the arguments is not used in the function. (since R2025a)The function
yp = ODEFcn(t,y,ydel,ypdel), whenEquationTypeis"delay"and for a scalart, column vectory, and matricesydelandypdel, must return a column vectorypthat corresponds to .ODEFcnmust accept at least four arguments,t,y,ydel,ypdel, even if one of the arguments is not used in the function. (since R2025a)
To supply parameter values, define ODEFcn as a function that
accepts three inputs, dydt = ODEFcn(t,y,p), four inputs, f
= ODEFcn(t,y,yp,p) or dydt = ODEFun(t,y,Z,p), or five
inputs, yp = ODEFcn(t,y,ydel,ypdel,p), and then use the
Parameters property to store parameter values (such as in a
struct or cell array).
For example, to solve a single equation , you can use the anonymous function @(t,y)
5*y-3.
For a system of equations, the output of ODEFcn is a vector.
Each element in the vector is the computed value of the right side of one equation.
For example, consider this system of two equations.
An anonymous function that defines these equations is @(t,y)
[y(1)+2*y(2); 3*y(1)+2*y(2)].
Example:
F.ODEFcn = @myFcn specifies a handle to a named function file
myFcn.m containing the equations.
Example: F.ODEFcn = @(t,y) [y(2); -y(1)] specifies an anonymous
function that defines a system of two equations.
Example: F.ODEFcn = @(t,y,yp) [yp(1)-y(2); yp(2)+1] specifies an
anonymous function that defines a system of two equations.
Example: F.ODEFcn = @(t,y,p) 5*y*p(1)-3*p(2) specifies an
anonymous function for a single equation that uses two parameters.
Data Types: function_handle
Initial time for integration, specified as a real scalar. The value of
InitialTime is the beginning of the integration interval where
the initial conditions specified in InitialValue are applied by
the solver before beginning integration steps.
Example:
F.InitialTime = 10;
Data Types: single | double
Value of solution at InitialTime, specified as a scalar or
vector. InitialValue must be a vector with the same length as the
output of ODEFcn so that an initial value is specified for each
equation defined in ODEFcn. The value of
InitialTime is the beginning of the integration interval where
the initial conditions specified in InitialValue are applied by
the solver before beginning integration steps.
Example:
F.InitialValue = 1;
Example:
F.InitialValue = [1 2 3];
Data Types: single | double
Complex Number Support: Yes
Equation parameters, specified as an array of any size or data type. The values
you store in Parameters can be supplied to any of the functions
used for the ODEFcn, Jacobian,
MassMatrix, or EventDefinition properties
by specifying an extra input argument in the function.
For instance, you can supply parameter values stored in the
Parameters property to ODEFcn by
specifying ODEFcn as a function handle that accepts three inputs,
dydt = ODEFcn(t,y,p). For example, F.ODEFcn = @(t,y,p)
5*y*p(1)-3*p(2) specifies an anonymous function for a single equation that
uses two parameters. If you then specify F.Parameters = [2 3], then
ODEFcn uses the parameter values p(1) = 2
and p(2) = 3 whenever the solver calls the function.
Example:
F.Parameters = [0.1 0.5] specifies two parameter
values.
Data Types: single | double
Complex Number Support: Yes
Mass matrix, specified as an odeMassMatrix object, matrix, or handle to a function that evaluates the
mass matrix.
ode objects can represent problems of the form , where is a mass matrix that can be full or sparse. The mass matrix encodes
linear combinations of derivatives on the left side of the equation.
When the mass matrix is nonsingular, the equation simplifies to and the ODE has a solution for any initial value. However, it is often more convenient and natural to express the model in terms of the mass matrix directly using , and avoiding the computation of the matrix inverse reduces the storage and execution time needed to solve the problem.
When the mass matrix is singular, then the problem is a system of differential algebraic equations (DAEs). A DAE has a solution only when the initial values are consistent; that is, you must specify the initial slope using the
InitialSlopeproperty such that the initial conditions are all consistent, . If the specified initial conditions are not consistent with theInitialTime,InitialValue, andMassMatrixproperties, then the solver treats them as guesses and attempts to compute consistent values for the initial slopes that are close to the guesses before continuing to solve the problem. For more information, see Solve Differential Algebraic Equations (DAEs).
You can specify the value of the MassMatrix property as:
An
odeMassMatrixobject, which represents the mass matrix and its associated properties. You can specify whether the mass matrix is singular or has state dependence.A constant matrix with calculated values for .
A handle to a function that computes the matrix elements and that accepts two input arguments,
M = Mass(t,y). To give the function access to parameter values stored in theParametersproperty, specify a third input argument in the function definition,M = Mass(t,y,p).
If you specify a matrix or function handle, then MATLAB converts it to an odeMassMatrix object.
Example: F.MassMatrix = @Mass specifies the function
Mass that evaluates the mass matrix.
Example: F.MassMatrix = [1 0; -2 1] specifies a constant mass
matrix.
Example: F.MassMatrix =
odeMassMatrix(MassMatrix=@Mass,StateDependence="strong",SparsityPattern=S)
specifies a state-dependent mass matrix and the sparsity pattern when the mass matrix
multiplies a vector.
Data Types: single | double | function_handle
Complex Number Support: Yes
Advanced Problem Definition
Since R2024b
Equation form, specified as one of these options:
"standard"for standard ordinary differential equations (ODEs)"fullyimplicit"for implicit ODEs, that is, a system of differential equations of the form . If you specify the Jacobian when theEquationTypeproperty is"fullyimplicit", the Jacobian must be a function handle or cell array."delay"for delay differential equations (DDEs), that is, a system of differential equations of the form , , or . (since R2025a)
Jacobian matrix, specified as an odeJacobian
object, matrix, cell array, or handle to a function that evaluates the Jacobian. The
Jacobian is a matrix of partial derivatives of the functions that define the system of
differential equations.
For stiff ODE problems, providing information about the Jacobian matrix is critical for reliability and efficiency of the solver. If you do not provide the Jacobian, then the ODE solver approximates it numerically using finite differences.
For large systems of equations where it is not feasible to provide the entire analytic Jacobian, you can specify the sparsity pattern of the Jacobian matrix instead. The solver uses the sparsity pattern to calculate a sparse Jacobian.
You can specify the Jacobian property as:
An
odeJacobianobject, which can represent either the Jacobian matrix or its sparsity pattern.A constant matrix with calculated values for .
When
EquationTypeis"fullyimplicit", a two-element cell array with calculated values for the constant Jacobian with respect toyin the first element andypin the second element. If you specify one of the elements as[], the ODE solver approximates the corresponding Jacobian numerically while taking the provided values in the other element into account. (since R2024b)A handle to a function that computes the matrix elements and that accepts two input arguments,
dfdy = Fjac(t,y). To give the function access to parameter values in theParametersproperty, specify a third input argument in the function definition,dfdy = Fjac(t,y,p).When
EquationTypeis"fullyimplicit", a handle to a function that computes the matrix elements and that accepts three input arguments,[dfdy,dfdp] = Fjac(t,y,yp). To give the function access to parameter values in theParametersproperty, specify a fourth input argument in the function definition,[dfdy,dfdp] = Fjac(t,y,yp,p). (since R2024b)
If you specify a matrix, function handle, or cell array, then
MATLAB converts it to an odeJacobian object.
Example: F.Jacobian = @Fjac specifies the function
Fjac that evaluates the Jacobian matrix.
Example: F.Jacobian = [0 1; -2 1] specifies a constant Jacobian
matrix.
Example: F.Jacobian = odeJacobian(SparsityPattern=S) specifies
the Jacobian sparsity pattern using sparse matrix S.
Data Types: single | double | function_handle
Complex Number Support: Yes
Events to detect, specified as an odeEvent
object. Create an odeEvent object to define expressions that trigger
an event when they cross zero. You can specify the direction of the zero crossing and
what to do when an event triggers, including the use of a callback function.
Nonnegative solution components, specified as a scalar index or vector of
indices. Use the NonNegativeVariables property to specify which
solutions the solver must keep nonnegative. If dydt = ODEFcn(t,y),
then the indices correspond to elements in the vector y. For
example, if you specify a value of 3, then the solver keeps the
solution component y(3) nonnegative.
Note
NonNegativeVariables is not available for the
ode23s solver. Additionally, for ode15s,
ode23t, and ode23tb the property is not
available for problems that have a mass matrix.
Example: F.NonNegativeVariables = [1 3] specifies that the first
and third solution components must be kept nonnegative.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Initial value of dy/dt, specified as a vector. Use this
property with the ode15s and ode23t solvers
when solving DAEs. The specified vector is the initial slope such that . If the specified initial conditions are not consistent with the
InitialTime, InitialValue, and
MassMatrix properties, then the solver treats them as guesses
and attempts to compute consistent values for the initial slopes that are close to the
guesses before continuing to solve the problem. For more information, see Solve Differential Algebraic Equations (DAEs).
Data Types: single | double
Sensitivity analysis information, specified as an odeSensitivity
object. The ODE solver performs sensitivity analysis only when the
Sensitivity property is nonempty. The analysis is with respect
to the Parameters property, which must be nonempty and numeric.
See odeSensitivity for more information.
Example: F.Sensitivity = odeSensitivity performs sensitivity
analysis on all parameters.
Example: F.Sensitivity = odeSensitivity(ParameterIndices=1:2)
performs sensitivity analysis on the first two parameters.
Since R2025a
DDE delay information, specified as an odeDelay object. To solve
a DDE using the ODE solver, you must specify the DelayDefinition
property. See odeDelay
for more information.
Example: F.DelayDefinition = odeDelay(ValueDelay=[2; 1],History=[0.1;
0.5]) specifies a DDE that has solution delays [2; 1]
and solution history [0.1; 0.5].
Since R2025a
Separate complex ODE equation into real and imaginary parts while solving,
specified as "off" or "on", or as a numeric or
logical 1 (true) or 0
(false). A value of "on" is equivalent to
true, and "off" is equivalent to
false. Thus, you can use the value of this property as a logical
value. The value is stored as an on/off logical value of type OnOffSwitchState.
When SeparateComplexParts is specified as
"on", each variable of the complex ODE equation is split into
real and imaginary parts while solving and then combined at the end. Use this property
when the ODE is complex and the selected solver fails or takes a long time to
converge. Specifying SeparateComplexParts is especially helpful
for solving implicit and stiff ODEs where the Jacobian is not specified. For more
information on how a complex ODE equation is split into real and imaginary parts, see
Complex ODEs.
Solver Control
Solver method, specified as one of the values in this table. To change the solver
based on specified parameters after creating an ode object, use the
selectSolver function. For example, you can incorporate a stiffness
detection heuristic when selecting a solver by using the
selectSolver function with its
DetectStiffness name-value argument.
| Value | Description |
|---|---|
| Automatically selects a solver based on available problem
information and tolerances. The |
| Similar to |
| Similar to |
| Runge-Kutta (2,3) pair. See |
| Runge-Kutta (4,5) pair. See |
| Runge-Kutta 8(7) pair with a 7th-order continuous extension. See
|
| Runge-Kutta 9(8) pair with an 8th-order continuous extension. See
|
| Variable-step, variable-order (VSVO) solver of orders 1 to 13. See
|
| Variable-step, variable-order (VSVO) solver based on the numerical
differentiation formulas (NDFs) of orders 1 to 5. See |
| Modified Rosenbrock formula of order 2. See |
| Trapezoidal rule using a “free” interpolant. See |
| Implicit Runge-Kutta formula with a trapezoidal rule step as its
first stage and a backward differentiation formula of order 2 as its second
stage. See |
| Variable-step, variable order (VSVO) solver based on the backward
differentiation formulas (BDFs) of orders 1 to 5. See |
| Variable-step, variable-order (VSVO) solver using Adams-Moulton formulas, with the order varying between 1 and 12. Supports sensitivity analysis. See CVODE and CVODES. |
| Variable-step, variable-order (VSVO) solver using backward differentiation formulas (BDFs) in fixed-leading coefficient form, with order varying between 1 and 5. Supports sensitivity analysis. See CVODE and CVODES. |
| Variable-order, variable-coefficient solver using backward differentiation formulas (BDFs) in fixed-leading coefficient form, with order varying between 1 and 5. Supports sensitivity analysis. See IDA and IDAS. |
| Runge-Kutta (2,3) pair. See |
| Fourth-order Runge-Kutta method. See |
| Neutral type delay solver. See |
This property is read-only.
Selected solver, returned as the name of a solver. If the value of
Solver is "auto",
"stiff", or "nonstiff", then the
ode object automatically chooses a solver and sets the value of
SelectedSolver to the name of the chosen solver. If you
manually select a solver, then SelectedSolver and
Solver have the same value.
Solver-specific options, specified as a matlab.ode.options.*
object. The ode object automatically populates the
SolverOptions property with an options object appropriate for
the selected solver. You can check available options for an existing
ode object with the command
properties(F.SolverOptions). Specify options for the ODE problem
by changing property values of the matlab.ode.options.* object. For
example, F.SolverOptions.OutputFcn = @odeplot specifies an output
function that the solver calls after each successful time step.
When the Solver property is "auto",
"stiff", or "nonstiff", the
SolverOptions property is read-only.
This table summarizes the available options for each solver.
| Options Object | Properties |
|---|---|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
Absolute error tolerance, specified as a positive scalar or vector. This tolerance
is a threshold below which the value of the solution becomes unimportant. If the
solution |y| is less than AbsoluteTolerance,
then the solver does not need to obtain any correct digits in |y|.
For this reason, keep in mind the scale of the solution components when setting the
value of AbsoluteTolerance.
If AbsoluteTolerance is a vector, then it must be the same
length as the number of solution components. If AbsoluteTolerance
is a scalar, then the value applies to all solution components.
At each step, the ODE solver estimates the local error e in the
ith component of the solution. To be successful, the step must
have an acceptable error, as determined by both the relative and absolute error
tolerances:
|e(i)| <= max(RelativeTolerance*abs(y(i)),AbsoluteTolerance(i))
Data Types: single | double
Relative error tolerance, specified as a positive scalar. This tolerance measures
the error relative to the magnitude of each solution component. The relative error
tolerance controls the number of correct digits in all solution components, except
those smaller than AbsoluteTolerance.
At each step, the ODE solver estimates the local error e in the
ith component of the solution. To be successful, the step must
have an acceptable error, as determined by both the relative and absolute error
tolerances:
|e(i)| <= max(RelativeTolerance*abs(y(i)),AbsoluteTolerance(i))
Data Types: single | double
Object Functions
solve | Solve ODE over interval or at specified points |
solutionFcn | Construct function that interpolates ODE solution |
selectSolver | Change ODE solver |
Examples
Create an empty ode object, and then specify values for the ODEFcn and InitialValue properties.
F = ode; F.ODEFcn = @(t,y) 2*t; F.InitialValue = 0;
Check which solver is selected for the problem, and then solve the equation over the time range [0 10].
F.SelectedSolver
ans =
SolverID enumeration
ode45
sol = solve(F,0,10)
sol =
ODEResults with properties:
Time: [0 0.2500 0.5000 0.7500 1 1.2500 1.5000 1.7500 2 2.2500 2.5000 2.7500 3 3.2500 3.5000 3.7500 4 4.2500 4.5000 4.7500 5 5.2500 5.5000 5.7500 6 6.2500 6.5000 6.7500 7 7.2500 7.5000 7.7500 8 8.2500 8.5000 8.7500 9 9.2500 9.5000 9.7500 10]
Solution: [0 0.0625 0.2500 0.5625 1.0000 1.5625 2.2500 3.0625 4 5.0625 6.2500 7.5625 9 10.5625 12.2500 14.0625 16 18.0625 20.2500 22.5625 25 27.5625 30.2500 33.0625 36 39.0625 42.2500 45.5625 49 52.5625 56.2500 60.0625 64 68.0625 … ] (1×41 double)
Plot the results.
plot(sol.Time,sol.Solution,"-o")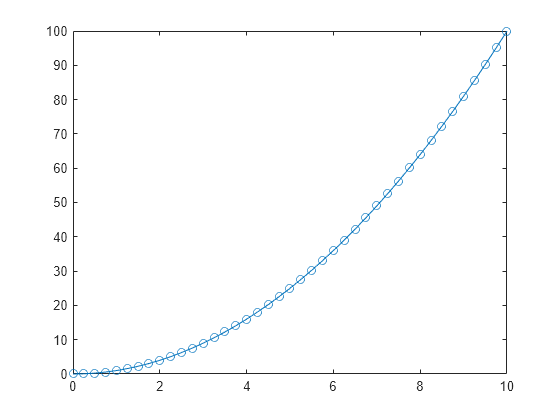
Create an ode object that represents the complex ODE with initial value . Specify the ODEFcn, InitialValue, and SeparateComplexParts properties.
F = ode;
F.ODEFcn = @(t,y) y.*t + 2*1i;
F.InitialValue = 1+1i;
F.SeparateComplexParts = "on";Solve the ODE over the time range [0 2].
sol = solve(F,0,2)
sol =
ODEResults with properties:
Time: [0 0.0251 0.0502 0.0754 0.1005 0.1505 0.2005 0.2505 0.3005 0.3505 0.4005 0.4505 0.5005 0.5505 0.6005 0.6505 0.7005 0.7505 0.8005 0.8505 0.9005 0.9505 1.0005 1.0505 1.1005 1.1505 1.2005 1.2505 1.3005 1.3505 1.4005 1.4505 … ] (1×45 double)
Solution: [1.0000 + 1.0000i 1.0003 + 1.0506i 1.0013 + 1.1018i 1.0028 + 1.1538i 1.0051 + 1.2067i 1.0114 + 1.3146i 1.0203 + 1.4267i 1.0319 + 1.5434i 1.0462 + 1.6655i 1.0633 + 1.7937i 1.0835 + 1.9287i 1.1068 + 2.0712i 1.1334 + 2.2223i … ] (1×45 double)
The Van der Pol oscillator equation is a second-order differential equation. The equation includes a parameter , and the equation becomes stiff when the value of is large.
Using the substitutions and produces a system of two first-order equations.
The Jacobian matrix for these equations is the matrix of partial derivatives of each equation with respect to both and .
Solve the Van der Pol oscillator using and initial values of [2; 0] by creating an ode object to represent the problem.
Store the value of in the
Parametersproperty.Specify the initial values in the
InitialValueproperty.Specify the system of equations in the
ODEFcnproperty, specifying three input arguments so that the value for is passed to the function.Specify a function that calculates the Jacobian matrix in the
Jacobianproperty, specifying three input arguments so that the value for is passed to the function.
F = ode; F.Parameters = 1000; F.InitialValue = [2; 0]; F.ODEFcn = @(t,y,p) [y(2); p(1)*(1-y(1)^2)*y(2)-y(1)]; F.Jacobian = @(t,y,p) [0 1; -2*p(1)*y(1)*y(2)-1 p(1)*(1-y(1)^2)];
Display the ode object. The SelectedSolver property shows that the ode15s solver was automatically chosen for this problem.
F
F =
ode with properties:
Problem definition
ODEFcn: @(t,y,p)[y(2);p(1)*(1-y(1)^2)*y(2)-y(1)]
Parameters: 1000
InitialTime: 0
InitialValue: [2×1 double]
Jacobian: [1×1 odeJacobian]
EquationType: standard
Solver properties
AbsoluteTolerance: 1.0000e-06
RelativeTolerance: 1.0000e-03
Solver: auto
SelectedSolver: ode15s
Show all properties
Solve the system of equations over the time interval [0 3000] by using the solve method. Plot the first solution component.
S = solve(F,0,3000);
plot(S.Time,S.Solution(1,:),"-o")
Create an ode object for the van der Pol equations with mu = 1000 using the built-in function file vdp1000.m. Specify the initial values of y' and y'' as 2 and 0, respectively.
F = ode(ODEFcn=@vdp1000,InitialValue=[2;0])
F =
ode with properties:
Problem definition
ODEFcn: @vdp1000
InitialTime: 0
InitialValue: [2×1 double]
EquationType: standard
Solver properties
AbsoluteTolerance: 1.0000e-06
RelativeTolerance: 1.0000e-03
Solver: auto
SelectedSolver: ode45
Show all properties
The automatically selected solver is ode45. Solve the ODE system over the time interval [0 3000]. Measure the time the ode45 solver takes by using tic and toc.
tic sol45 = solve(F,0,3000); toc
Elapsed time is 17.243319 seconds.
Call the selectSolver function with the DetectStiffness name-value argument to choose a solver using a stiffness detection heuristic. Also specify the IntervalLength name-value argument as 3000.
F.Solver = selectSolver(F,DetectStiffness="on",IntervalLength=3000)F =
ode with properties:
Problem definition
ODEFcn: @vdp1000
InitialTime: 0
InitialValue: [2×1 double]
Jacobian: []
EquationType: standard
Solver properties
AbsoluteTolerance: 1.0000e-06
RelativeTolerance: 1.0000e-03
Solver: ode15s
Show all properties
The selected solver is now ode15s. Solving the ODE system over the time interval [0 3000] using the ode15s solver is faster and more efficient than using the ode45 solver.
tic sol15s = solve(F,0,3000); toc
Elapsed time is 0.244035 seconds.
Consider this system of first-order equations.
The left side of the equations contain time derivatives, . However, because the derivative for does not appear in the system, the equations define a system of differential algebraic equations. Rewriting the system in the form shows a constant, singular mass matrix on the left side.
Solve the system of equations using the initial values [1 1 -2] by creating an ode object to represent the problem.
Specify the initial values in the
InitialValueproperty.Specify the system of equations as an anonymous function in the
ODEFcnproperty.Use an
odeMassMatrixobject to specify the constant, singular mass matrix in theMassMatrixproperty.
F = ode;
F.InitialValue = [1 1 -2];
F.ODEFcn = @(t,y) [y(1)*y(3)-y(2);
y(1)-1;
y(1)+y(2)+y(3)];
F.MassMatrix = odeMassMatrix(MassMatrix=[1 0 0; 0 1 0; 0 0 0],Singular="yes");Display the ode object. The SelectedSolver property shows that the ode15s solver was automatically chosen for this problem.
F
F =
ode with properties:
Problem definition
ODEFcn: @(t,y)[y(1)*y(3)-y(2);y(1)-1;y(1)+y(2)+y(3)]
InitialTime: 0
InitialValue: [1 1 -2]
Jacobian: []
MassMatrix: [1×1 odeMassMatrix]
EquationType: standard
Solver properties
AbsoluteTolerance: 1.0000e-06
RelativeTolerance: 1.0000e-03
Solver: auto
SelectedSolver: ode15s
Show all properties
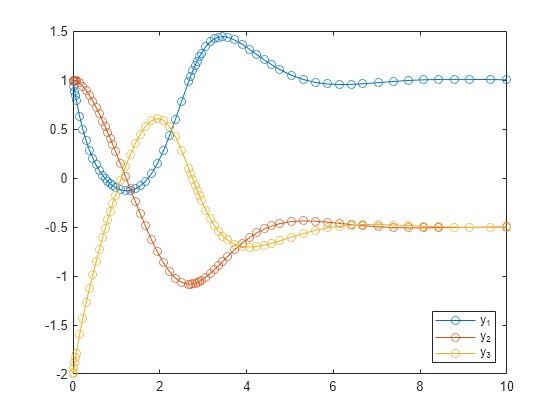
Solve the system of equations over the time interval [0 10] by using the solve method. Plot all three solution components.
S = solve(F,0,10); plot(S.Time,S.Solution,"-o") legend("y_1","y_2","y_3",Location="southeast")
Solve an ODE system with two equations and two parameters, and perform sensitivity analysis on the parameters.
Create an ode object to represent this system of equations.
Specify the initial conditions as and , and parameter values of and . To enable sensitivity analysis of the parameters, set the Sensitivity property of the ode object to an odeSensitivity object.
p = [0.05 1.5]; F = ode(ODEFcn=@(t,y,p) [p(1)*y(1)-y(2); -p(2)*y(2)], ... InitialValue=[2 3], ... Parameters=p, ... Sensitivity=odeSensitivity)
F =
ode with properties:
Problem definition
ODEFcn: @(t,y,p)[p(1)*y(1)-y(2);-p(2)*y(2)]
Parameters: [0.0500 1.5000]
InitialTime: 0
InitialValue: [2 3]
Sensitivity: [1×1 odeSensitivity]
EquationType: standard
Solver properties
AbsoluteTolerance: 1.0000e-06
RelativeTolerance: 1.0000e-03
Solver: auto
SelectedSolver: cvodesnonstiff
Show all properties
Because the equations are nonstiff and sensitivity analysis is enabled, the ode object automatically chooses the cvodesnonstiff solver for this problem.
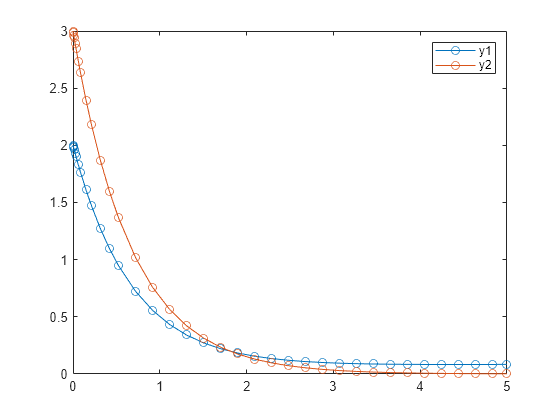
Solve the ODE over the time interval [0 5], and plot the solution for each component.
S = solve(F,0,5)
S =
ODEResults with properties:
Time: [0 2.9540e-09 2.9543e-05 2.2465e-04 4.1976e-04 0.0024 0.0080 0.0137 0.0245 0.0353 0.0611 0.0869 0.1499 0.2129 0.3169 0.4208 0.5248 0.7204 0.9161 1.1118 1.3075 1.5031 1.6988 1.8945 2.0901 2.2858 2.4815 2.6772 2.8728 … ] (1×40 double)
Solution: [2×40 double]
Sensitivity: [2×2×40 double]
plot(S.Time,S.Solution(1,:),"-o",S.Time,S.Solution(2,:),"-o") legend("y1","y2")
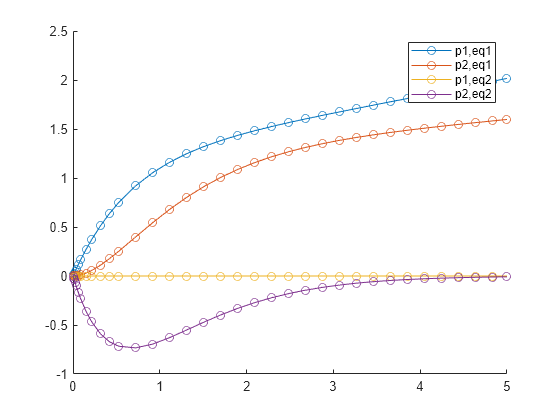
The values in S.Sensitivity are partial derivatives of the equations with respect to the parameters. To examine the effects of the parameter values during the integration, plot the sensitivity values.
figure hold on plot(S.Time,squeeze(S.Sensitivity(1,1,:)),"-o") plot(S.Time,squeeze(S.Sensitivity(1,2,:)),"-o") plot(S.Time,squeeze(S.Sensitivity(2,1,:)),"-o") plot(S.Time,squeeze(S.Sensitivity(2,2,:)),"-o") legend("p1,eq1","p2,eq1","p1,eq2","p2,eq2") hold off
Consider a ball thrown upward with an initial velocity . The ball is subject to acceleration due to gravity aimed downward, so its acceleration is
Rewriting the equation as a first-order system of equations with the substitutions and yields
Solve the equations for the position and velocity of the ball over time.
Define Equations and Initial Conditions
Create a function handle for the first-order system of equations that accepts two inputs for (t,y). Use the value for the acceleration due to gravity.
dydt = @(t,y) [y(2); -9.8];
Next, create a vector with the initial conditions. The ball starts at position at as it is thrown upward with initial velocity .
y0 = [3 20];
Model Ball Bounces as Events
The ball initially travels upward until the force due to gravity causes it to change direction and head back down to the ground. If you solve the equations without more consideration, then the ball falls back downward forever without striking the ground. Instead, you can use an event function to detect when the position of the ball goes to zero where the ground is located. Because the solution component is the position of the ball, the event function tracks the value of so that an event triggers whenever .
Create a function handle for the event function that accepts two inputs for (t,y).
bounceEvent = @(t,y) y(1);
When the ball strikes the ground, its direction changes again as it heads back upwards with a new (smaller) initial velocity. To model this situation, use a callback function along with the event function. When an event triggers, the ODE solver invokes the callback function. The callback function resets the position and initial velocity of the ball so that the integration can restart with the correct initial conditions. When an event occurs, the callback function sets the position and attenuates the velocity by a factor of while reversing its direction back upward. Define a callback function that performs these actions.
function [stop,y] = bounceResponse(t,y) stop = false; y(1) = 0; y(2) = -0.9*y(2); end
(The callback function is included as a local function at the end of the example.)
Create an odeEvent object to represent the bouncing ball events. Specify Direction="descending" so that only events where the position is decreasing are detected. Also, specify Response="callback" so that the solver invokes the callback function when an event occurs.
E = odeEvent(EventFcn=bounceEvent, ... Direction="descending", ... Response="callback", ... CallbackFcn=@bounceResponse)
E =
odeEvent with properties:
EventFcn: @(t,y)y(1)
Direction: descending
Response: callback
CallbackFcn: @bounceResponse
Solve Equations
Create an ode object for the problem, specifying the equations dydt, initial conditions y0, and events E as property values.
F = ode(ODEFcn=dydt,InitialValue=y0,EventDefinition=E);
Integrate the equations over the time interval [0 30] by using the solve method. Specify Refine=8 to generate 8 points per step. The resulting object has properties for the time and solution, and because events are being tracked, the object also displays properties related to the events that triggered during the integration.
S = solve(F,0,30,Refine=8)
S =
ODEResults with properties:
Time: [0 0.0038 0.0075 0.0113 0.0151 0.0188 0.0226 0.0264 0.0301 0.0490 0.0678 0.0867 0.1055 0.1243 0.1432 0.1620 0.1809 0.2751 0.3692 0.4634 0.5576 0.6518 0.7460 0.8402 0.9344 1.3094 1.6844 2.0594 2.4344 2.8094 3.1844 … ] (1×468 double)
Solution: [2×468 double]
EventTime: [4.2265 8.1607 11.7015 14.8882 17.7563 20.3375 22.6606 24.7514 26.6331 28.3267 29.8509]
EventSolution: [2×11 double]
EventIndex: [1 1 1 1 1 1 1 1 1 1 1]
Plot Results
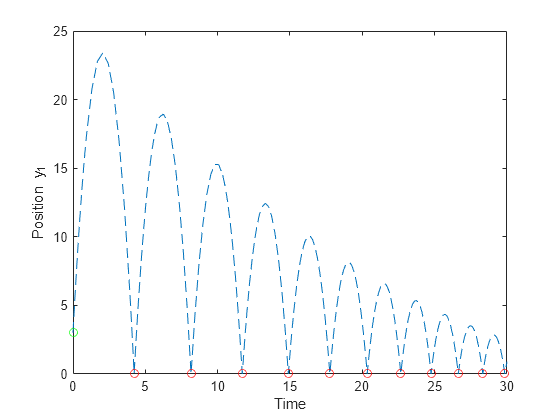
Plot the position of the ball over time, marking the initial position with a green circle and events with red circles.
plot(S.Time,S.Solution(1,:),"--") hold on plot(S.EventTime,S.EventSolution(1,:),"ro") plot(0,y0(1),"go") hold off ylim([0 25]) xlabel("Time") ylabel("Position y_1")
Local Functions
function [stop,y] = bounceResponse(t,y) stop = false; y(1) = 0; y(2) = -0.9*y(2); end
Version History
Introduced in R2023bFor properties that accept matrix values, you can now specify single-precision sparse
matrices. Additionally, for properties that accept function handles, the specified functions
can now return single-precision outputs. If you specify any property as
single, the properties of the ODEResults object returned
by solve and solutionFcn are single. For faster
computation, specify all property values and function handle outputs using as the same
precision.
You can solve delay differential equations (DDEs) using an ode object
by specifying the Solver property as "dde23",
"ddesd", or "ddensd" and specifying the
DelayDefinition property as an odeDelay object. If
you specify only DelayDefinition and not Solver,
the ode object automatically selects a solver.
You can solve ODEs with complex solution values using the ode object by
specifying the SeparateComplexParts property as
"on". Specify SeparateComplexParts as
"on" when the ODE is complex and the selected solver fails or takes a
long time to converge. This is especially helpful for solving implicit and stiff ODEs where
the Jacobian is not specified.
You can now specify the Solver property as
"ode15i" for implicit ODEs. Alternatively, you can specify whether your
ODE is implicit by setting the new EquationType property to
"standard" (default) or "fullyimplicit".
If you specify the Jacobian when EquationType is
"fullyimplicit", the Jacobian must be a function handle or cell array.
Additionally, the ODEFcn property can accept functions of the form
f = ODEFcn(t,y,yp) for implicit ODEs.
You can specify parameters to change the solver after creating an ode
object by using the selectSolver object function. For example, you can incorporate a stiffness
detection heuristic when selecting a solver by using the selectSolver
function with its DetectStiffness name-value argument.
See Also
Objects
Live Editor Tasks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)