surface
Gráfica de superficie primitiva
Sintaxis
Descripción
surface( crea una gráfica de superficie primitiva tridimensional. La función representa los valores en la matriz X,Y,Z)Z como alturas sobre una cuadrícula en el plano x-y que definen X e Y. El color de la superficie varía según las alturas que especifique Z.
A diferencia de surf, la función primitiva surface no llama a newplot antes de la representación y no respeta el valor de la propiedad NextPlot para la figura o los ejes. En cambio, añade la gráfica de superficie a los ejes actuales sin eliminar otros objetos de gráficas ni restablecer las propiedades de los ejes.
surface( crea una gráfica de superficie primitiva y usa los índices de columna y de fila de los elementos de Z)Z como coordenadas x e y.
surface( representa en los ejes que especifica ax,___)ax en lugar de en los ejes actuales. Especifique los ejes como primer argumento de entrada.
surface(___, especifica las propiedades de superficie utilizando uno o más argumentos de par nombre-valor. Por ejemplo, Name,Value)'FaceAlpha',0.5 crea una superficie semitransparente.
s = surface(___) devuelve el objeto de superficie primitiva de la gráfica. Utilice s para modificar la superficie después de crearla. Para obtener una lista de las propiedades, consulte Surface Properties.
Ejemplos
Cree tres matrices del mismo tamaño. Después, represéntelas como una superficie. La superficie utiliza Z tanto para la altura como para el color.
[X,Y] = meshgrid(1:0.5:10,1:20); Z = sin(X) + cos(Y); surface(X,Y,Z)

De forma predeterminada, la superficie se muestra en los ejes utilizando una vista bidimensional. Cambie los ejes a una vista tridimensional.
view(3)
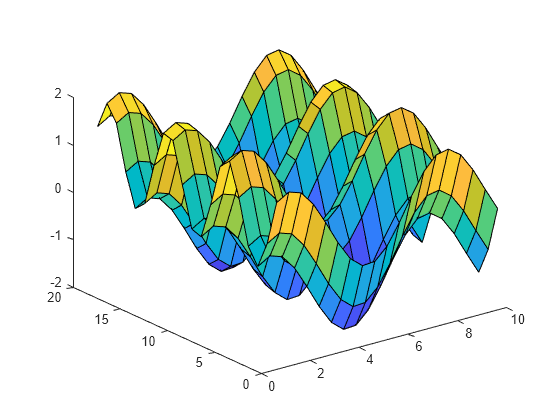
Especifique los colores para una gráfica de superficie incluyendo una cuarta entrada de matriz, C. La gráfica de malla utiliza Z para la altura y C para el color. Especifique los colores utilizando un mapa de colores, que usa números únicos para representar los colores de un espectro. Cuando utilice un mapa de colores, C tiene el mismo tamaño que Z. Añada una barra de colores a la gráfica para mostrar cómo los valores de los datos de C se corresponden con los colores en el mapa de colores, y establezca la vista de la gráfica en la vista tridimensional predeterminada.
[X,Y] = meshgrid(1:0.5:10,1:20); Z = sin(X) + cos(Y); C = X.*Y; surface(X,Y,Z,C) colorbar view(3)

Cree una superficie semitransparente especificando el par nombre-valor FaceAlpha con 0.5 como valor. Para permitir más modificaciones, asigne el objeto de superficie a la variable s.
[X,Y] = meshgrid(-5:.5:5);
Z = Y.*sin(X) - X.*cos(Y);
s = surface(X,Y,Z,'FaceAlpha',0.5);
view(3)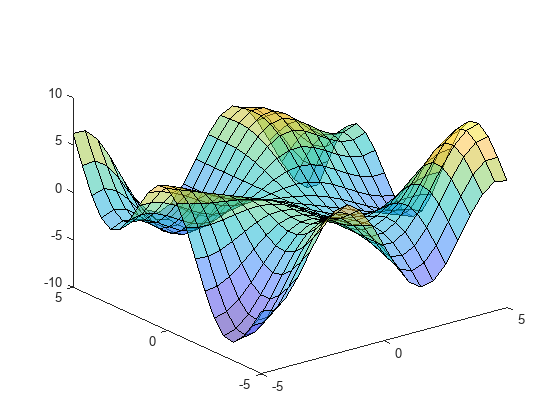
Utilice s para acceder y modificar las propiedades de un objeto de superficie después de crearlo. Por ejemplo, oculte los bordes estableciendo la propiedad EdgeColor.
s.EdgeColor = 'none';
Cree una superficie y muestre una imagen en ella.
Cree tres matrices del mismo tamaño.
[pX,pY,pZ] = peaks(25);
Cargue un conjunto de datos que contenga una imagen de la Tierra. Los datos de la imagen aparecen en una variable del área de trabajo X, y el mapa de colores asociado aparece en map.
load earth
whoYour variables are: X map pX pY pZ
Cree una gráfica de superficie y visualice la imagen a lo largo de la superficie. Dado que los datos de superficie pZ y los datos de color X tienen tamaños diferentes, establezca la superficie FaceColor en 'texturemap'. Establezca la vista de la gráfica en la vista tridimensional predeterminada.
surface(pX,pY,pZ,X,'FaceColor','texturemap', ... 'EdgeColor','none','CDataMapping','direct') colormap(map) view(3)

Argumentos de entrada
Coordenadas x, especificadas como matriz del mismo tamaño que Z o como vector con una longitud n, en el que [m,n] = size(Z). Si no especifica valores para X e Y, surface utiliza los vectores (1:n) y (1:m).
Puede usar la función meshgrid para crear matrices X e Y.
La propiedad XData del objeto Surface guarda las coordenadas x.
Ejemplo: X = 1:10
Ejemplo: X = [1 2 3; 1 2 3; 1 2 3]
Ejemplo: [X,Y] = meshgrid(-5:0.5:5)
Tipos de datos: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration
Coordenadas y, especificadas como matriz del mismo tamaño que Z o como vector con una longitud m, en el que [m,n] = size(Z). Si no especifica valores para X e Y, surface utiliza los vectores (1:n) y (1:m).
Puede usar la función meshgrid para crear las matrices X e Y.
La propiedad YData del objeto de superficie guarda las coordenadas y.
Ejemplo: Y = 1:10
Ejemplo: Y = [1 1 1; 2 2 2; 3 3 3]
Ejemplo: [X,Y] = meshgrid(-5:0.5:5)
Tipos de datos: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration
Coordenadas z, especificadas como matriz. Z debe tener al menos dos filas y dos columnas.
Z especifica la altura de la gráfica de superficie en cada coordenada x-y. Si no especifica los colores, Z también especifica los colores de superficie.
La propiedad ZData del objeto de superficie guarda las coordenadas z.
Ejemplo: Z = [1 2 3; 4 5 6]
Ejemplo: Z = sin(x) + cos(y)
Tipos de datos: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration
Arreglo de colores, especificado como matriz m por n de índices del mapa de colores o como arreglo m por n por 3 de tripletes RGB, en el que Z es m por n.
Para usar colores del mapa de colores, especifique
Ccomo matriz.Cindica un color en el mapa de colores en cada punto de cuadrícula de la superficie. La propiedadCDataMappingdel objeto de superficie controla cómo se corresponden los valores deCcon colores en el mapa de colores.Para usar colores de color real, especifique
Ccomo arreglo de tripletes RGB.
Para obtener más información, consulte Diferencias entre los mapas de colores y el color real.
La propiedad CData del objeto de superficie guarda el arreglo de colores. Para tener un mayor control sobre el color de la superficie, utilice las propiedades FaceColor y EdgeColor.
Ejes en los que representar, especificados como un objeto Axes o PolarAxes. Si no especifica los ejes, surface representa en los ejes actuales o crea un objeto Axes (ejes cartesianos).
Argumentos de par nombre-valor
Especifique pares opcionales de argumentos como Name1=Value1,...,NameN=ValueN, donde Name es el nombre del argumento y Value es el valor correspondiente. Los argumentos nombre-valor deben aparecer después de otros argumentos, pero el orden de los pares no importa.
En las versiones anteriores a R2021a, utilice comas para separar cada nombre y valor, y encierre Name entre comillas.
Ejemplo: surface(X,Y,Z,'FaceAlpha',0.5,'EdgeColor','none') crea una superficie semitransparente sin bordes dibujados.
Nota
Las propiedades que se enumeran aquí son solo un subconjunto. Para obtener una lista completa, consulte Surface Properties.
Color de línea de borde, especificado como uno de los valores enumerados en esta tabla.
| Valor | Descripción |
|---|---|
'none' | No dibuje los bordes. |
'flat' | Utilice un color diferente para cada borde según los valores en la propiedad
|
'interp' | Utilice colores interpolados para cada borde según los valores en la propiedad
|
| Triplete RGB, código de color hexadecimal o nombre del color | Utilice el color especificado para todos los bordes. Esta opción no incluye los valores de color en la propiedad
|
Los tripletes RGB y los códigos de color hexadecimales son útiles para especificar colores personalizados.
Un triplete RGB es un vector fila de tres elementos, cuyos elementos especifican las intensidades de los componentes rojo, verde y azul del color. Las intensidades deben estar en el rango
[0,1]; por ejemplo,[0.4 0.6 0.7].Un código de color hexadecimal es un vector de caracteres o un escalar de cadena que comienza con el símbolo de almohadilla (
#) seguido de tres o seis dígitos hexadecimales, que pueden oscilar entre0yF. Los valores no distinguen entre mayúsculas y minúsculas. Así, los códigos de color"#FF8800","#ff8800","#F80"y"#f80"son equivalentes.
Como alternativa, puede especificar algunos colores frecuentes por su nombre. En esta tabla se enumeran las opciones de color con su nombre, los tripletes RGB equivalentes y los códigos de color hexadecimales.
| Nombre del color | Nombre corto | Triplete RGB | Código de color hexadecimal | Apariencia |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan" | "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
En esta tabla, se enumeran las paletas de colores predeterminados para las gráficas en los temas claro y oscuro.
| Paleta | Colores de la paleta |
|---|---|
Antes de R2025a: La mayoría de las gráficas utilizan estos colores de forma predeterminada. |
|
|
|
Puede obtener los tripletes RGB y los códigos de color hexadecimales de estas paletas usando las funciones orderedcolors y rgb2hex. Por ejemplo, puede obtener los tripletes RGB de la paleta "gem" y convertirlos en códigos de color hexadecimales.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Antes de R2023b: Obtenga los tripletes RGB usando RGB = get(groot,"FactoryAxesColorOrder").
Antes de R2024a: Obtenga los códigos de color hexadecimales usando H = compose("#%02X%02X%02X",round(RGB*255)).
Estilo de línea, especificado como una de las opciones enumeradas en esta tabla.
| Estilo de línea | Descripción | Línea resultante |
|---|---|---|
"-" | Línea continua |
|
"--" | Línea discontinua |
|
":" | Línea de puntos |
|
"-." | Línea de puntos y rayas |
|
"none" | Sin línea | Sin línea |
Color de cara, especificado como uno de los valores de esta tabla.
| Valor | Descripción |
|---|---|
'flat' | Utilice un color diferente para cada cara según los valores en la propiedad
|
'interp' | Utilice colores interpolados para cada cara según los valores en la propiedad
|
| Triplete RGB, código de color hexadecimal o nombre del color | Utilice el color especificado para todas las caras. Esta opción no incluye los valores de color en la propiedad
|
'texturemap' | Transforme los datos de color de CData, para que se adapte a la superficie. |
'none' | No dibuje las caras. |
Los tripletes RGB y los códigos de color hexadecimales son útiles para especificar colores personalizados.
Un triplete RGB es un vector fila de tres elementos, cuyos elementos especifican las intensidades de los componentes rojo, verde y azul del color. Las intensidades deben estar en el rango
[0,1]; por ejemplo,[0.4 0.6 0.7].Un código de color hexadecimal es un vector de caracteres o un escalar de cadena que comienza con el símbolo de almohadilla (
#) seguido de tres o seis dígitos hexadecimales, que pueden oscilar entre0yF. Los valores no distinguen entre mayúsculas y minúsculas. Así, los códigos de color"#FF8800","#ff8800","#F80"y"#f80"son equivalentes.
Como alternativa, puede especificar algunos colores frecuentes por su nombre. En esta tabla se enumeran las opciones de color con su nombre, los tripletes RGB equivalentes y los códigos de color hexadecimales.
| Nombre del color | Nombre corto | Triplete RGB | Código de color hexadecimal | Apariencia |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan" | "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
En esta tabla, se enumeran las paletas de colores predeterminados para las gráficas en los temas claro y oscuro.
| Paleta | Colores de la paleta |
|---|---|
Antes de R2025a: La mayoría de las gráficas utilizan estos colores de forma predeterminada. |
|
|
|
Puede obtener los tripletes RGB y los códigos de color hexadecimales de estas paletas usando las funciones orderedcolors y rgb2hex. Por ejemplo, puede obtener los tripletes RGB de la paleta "gem" y convertirlos en códigos de color hexadecimales.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Antes de R2023b: Obtenga los tripletes RGB usando RGB = get(groot,"FactoryAxesColorOrder").
Antes de R2024a: Obtenga los códigos de color hexadecimales usando H = compose("#%02X%02X%02X",round(RGB*255)).
Transparencia de cara, especificada como uno de estos valores:
Escalar en el intervalo
[0,1]: utiliza una transparencia uniforme en todas las caras. Un valor de1es totalmente opaco y0es totalmente transparente. Los valores situados entre0y1son semitransparentes. Esta opción no utiliza los valores de transparencia en la propiedadAlphaData.'flat': utiliza una transparencia diferente para cada cara según los valores en la propiedadAlphaData. El valor de transparencia del primer vértice determina la transparencia de toda la cara. En primer lugar, debe especificar la propiedadAlphaDatacomo matriz del mismo tamaño que la propiedadZData. La propiedadFaceColortambién se debe establecer en'flat'.'interp': utilice transparencia interpolada para cada cara según los valores de la propiedadAlphaData. La transparencia varía en cada cara interpolando los valores en los vértices. En primer lugar, debe especificar la propiedadAlphaDatacomo matriz del mismo tamaño que la propiedadZData. La propiedadFaceColortambién se debe establecer en'interp'.'texturemap': transforma los datos deAlphaData, para que se adapten a la superficie.
Efecto de los objetos de luz en las caras, especificado como uno de estos valores:
'flat': aplica la luz uniformemente en toda la cara. Utilice este valor para ver objetos con caras.'gouraud': varía la luz en las distintas caras. Calcula la luz en los vértices y, después, interpola linealmente la luz en las distintas caras. Utilice este valor para ver superficies curvas.'none': no aplica luz de objetos de luz a las caras.
Para añadir un objeto de luz a los ejes, utilice la función light.
Nota
Se ha eliminado el valor 'phong'. En su lugar, utilice 'gouraud'.
Historial de versiones
Introducido antes de R2006aCree gráficas de superficie en coordenadas polares especificando un objeto PolarAxes como primer argumento.
Consulte también
Funciones
Propiedades
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)



















