Representar datos como una superficie

La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

Funciones para representar cuadrículas de datos

Las gráficas MATLAB^® definen una superficie a partir de las coordenadas z de puntos en una cuadrícula rectangular del plano x-y. La gráfica se forma uniendo puntos adyacentes con líneas rectas. Las gráficas de superficie son útiles para visualizar matrices que son demasiado grandes para mostrarse en forma numérica y para representar funciones de dos variables.

MATLAB puede crear diferentes formas de gráficas de superficie. Las gráficas de malla son superficies de malla que colorean solo las líneas que conectan los puntos de definición. Las gráficas de superficie muestran tanto las líneas de conexión como las caras de la superficie en color. En esta tabla se enumeran las distintas formas que pueden adoptar.

Función	Se usa para crear
`mesh`, `surf`	Gráfica de superficie
`meshc`, `surfc`	Gráfica de superficie con diagrama de contorno debajo
`meshz`	Gráfica de superficie con diagrama de cortina (plano de referencia)
`pcolor`	Gráfica de superficie plana (el valor solo es proporcional al color)
`surfl`	Gráfica de superficie iluminada desde la dirección especificada
`surface`	Función de bajo nivel (en la que se basan las funciones de alto nivel) para crear objetos de gráficas de superficie

Funciones de cuadrícula e interpolación de datos

Estas funciones son útiles cuando tiene que reestructurar e interpolar datos para poder representarlos como una superficie.

Función	Se usa para crear
`meshgrid`	Cuadrícula rectangular en espacio en 2D y 3D
`griddata`	Interpolar datos dispersos
`griddedInterpolant`	Interpolante para datos de malla
`scatteredInterpolant`	Interpolar datos dispersos

Para ver un análisis más detallado acerca de cómo interpolar datos, consulte Interpolating Gridded Data y Interpolating Scattered Data.

Gráficas de malla y de superficie

Los comandos mesh y surf crean gráficas de superficie en 3D de datos de matrices. Si Z es una matriz cuyos elementos Z(i,j) definen la altura de una superficie sobre una cuadrícula (i,j) subyacente, entonces

mesh(Z)

genera una vista de malla coloreada de la superficie y la muestra en una vista en 3D. De forma similar,

surf(Z)

genera una vista coloreada, con caras, de la superficie y la muestra en una vista en 3D. Normalmente, las caras son cuadriláteros, cada uno de un color constante, contorneado con líneas de malla negras, pero el comando shading permite eliminar las líneas de malla (shading flat) o seleccionar un sombreado interpolado en la cara (shading interp).

Las propiedades de objetos de superficie proporcionan controles adicionales sobre el aspecto visual de la superficie. Puede especificar estilos de líneas de borde, marcadores de vértices, coloreado de caras, características de iluminación, etc.

Visualización de funciones de dos variables

Para mostrar una función de dos variables, z = f (x,y), genere las matrices X e Y, que constan de filas y columnas repetidas, respectivamente, sobre el dominio de la función. Utilizará estas matrices para evaluar y representar la función.
La función meshgrid transforma el dominio especificado por dos vectores x e y en matrices X e Y. A continuación, usará estas matrices para evaluar funciones de dos variables: Las filas de X son copias del vector x y las columnas de Y son copias del vector y.

Ejemplo 1. Ejemplo: Ilustrar el uso de meshgrid

Para ilustrar el uso de meshgrid, considere la función sin(r)/r o sinc. Para evaluar esta función entre -8 y 8 tanto en x como en y, solo tiene que pasar un argumento de vector a meshgrid, que luego se usa en ambas direcciones.

[X,Y] = meshgrid(-8:.5:8);
R = sqrt(X.^2 + Y.^2) + eps;

La matriz R contiene la distancia desde el centro de la matriz, que es el origen. Añadir eps evita la división entre cero (en el paso siguiente) que produce valores Inf en los datos.

Formar la función sinc y representar Z con mesh da lugar a la superficie en 3D.

Z = sin(R)./R;
figure
mesh(X,Y,Z)

Eliminación de líneas ocultas

De forma predeterminada, MATLAB elimina las líneas ocultas en las gráficas de malla, aunque las caras de la gráfica no estén rellenas. Puede desactivar la eliminación de líneas ocultas y permitir que las caras de una gráfica de malla sean transparentes con el comando hidden:

hidden off

Destacar la forma de la superficie

MATLAB ofrece varias técnicas que pueden mejorar el contenido informativo de sus gráficas. Por ejemplo, la siguiente gráfica de la función sinc usa los mismos datos que la gráfica anterior, pero utiliza iluminación, ajustes de vista y un mapa de colores diferente para destacar la forma de la función representada (daspect, axis, view, camlight).

figure
colormap hsv
surf(X,Y,Z,'FaceColor','interp',...
   'EdgeColor','none',...
   'FaceLighting','gouraud')
daspect([5 5 1])
axis tight
view(-50,30)
camlight left

Consulte la función surf para obtener más información sobre gráficas de superficie.

Gráficas de superficie de datos muestreados de manera no uniforme

Puede usar meshgrid para crear una cuadrícula de puntos de datos muestreados de manera uniforme en los que evaluar y representar la función sinc. A continuación, MATLAB construye la gráfica de la superficie, conectando elementos de matriz vecinos para formar una malla de cuadriláteros.

Para producir una gráfica de superficie a partir de datos muestreados de manera no uniforme, utilice scatteredInterpolant para interpolar los valores en puntos espaciados uniformemente y, a continuación, use mesh y surf de la forma habitual.

Ejemplo: mostrar datos no uniformes en una superficie

El siguiente ejemplo evalúa la función sinc en puntos aleatorios dentro de un intervalo específico y, a continuación, genera datos muestreados de manera uniforme para mostrarlos como una gráfica de superficie. El proceso incluye las siguientes tareas:

Use linspace para generar valores espaciados uniformemente sobre el intervalo de datos muestreados de manera desigual.
Use meshgrid para generar la cuadrícula de representación con la salida de linspace.
Use scatteredInterpolant para interpolar los datos muestreados irregularmente en la cuadrícula espaciada regularmente devuelta por meshgrid.
Use una función de representación para mostrar los datos.

Genere datos muestreados de manera desigual dentro del intervalo [-8, 8] y úselos para evaluar la función:
```
x = rand(100,1)*16 - 8;
y = rand(100,1)*16 - 8;
r = sqrt(x.^2 + y.^2) + eps;
z = sin(r)./r;
```
La función linspace proporciona una forma apropiada de crear datos espaciados de manera uniforme con el número de elementos deseado. Las siguientes instrucciones producen vectores sobre el intervalo de los datos aleatorios con la misma resolución que la generada por la instrucción -8:.5:8 del ejemplo sinc anterior:
```
xlin = linspace(min(x),max(x),33);
ylin = linspace(min(y),max(y),33);
```
A continuación, utilice estos puntos para generar una cuadrícula espaciada de manera uniforme:
```
[X,Y] = meshgrid(xlin,ylin);
```
La clave de este proceso es usar scatteredInterpolant para interpolar los valores de la función en los puntos espaciados de manera uniforme, según los valores de la función en los puntos de datos originales (que son aleatorios en este ejemplo). Esta instrucción utiliza la interpolación lineal predeterminada para generar los nuevos datos:
```
f = scatteredInterpolant(x,y,z);
Z = f(X,Y);
```

Represente los datos interpolados y los no uniformes para producir:

figure
mesh(X,Y,Z) %interpolated
axis tight; hold on
plot3(x,y,z,'.','MarkerSize',15) %nonuniform

Remodelar datos

Suponga que tiene una recopilación de datos con los siguientes tripletes (X, Y, Z):

X	Y	Z
1	1	152
2	1	89
3	1	100
4	1	100
5	1	100
1	2	103
2	2	0
3	2	100
4	2	100
5	2	100
1	3	89
2	3	13
3	3	100
4	3	100
5	3	100
1	4	115
2	4	100
3	4	187
4	4	200
5	4	111
1	5	100
2	5	85
3	5	111
4	5	97
5	5	48

Puede representar datos que estén en forma de vector con varios tipos de gráficas de MATLAB, como surf, contour y stem3, reestructurando los datos primero. Use los valores (X, Y) para definir las coordenadas en un plano x-y en las que hay un valor Z. Las funciones reshape y transpose pueden reestructurar los datos de modo que los tripletes (X, Y, Z) formen una cuadrícula rectangular:

x = reshape(X,5,5)';
y = reshape(Y,5,5)';
z = reshape(Z,5,5)';

Remodelar los datos da como resultado tres arreglos de 5 por 5:

x =

     1     2     3     4     5
     1     2     3     4     5
     1     2     3     4     5
     1     2     3     4     5
     1     2     3     4     5

y =

     1     1     1     1     1
     2     2     2     2     2
     3     3     3     3     3
     4     4     4     4     4
     5     5     5     5     5

z =

   152    89   100   100   100
   103     0   100   100   100
    89    13   100   100   100
   115   100   187   200   111
   100    85   111    97    48

Ahora, puede representar los valores de Z con respecto a X e Y. Por ejemplo, cree una gráfica de tallos 3D:

stem3(x,y,z,'MarkerFaceColor','g')

Superficies paramétricas

Las funciones que dibujan superficies pueden tomar dos argumentos vectoriales o matriciales adicionales para describir superficies con datos x e y específicos. Si Z es una matriz de m por n, x es un vector de n, e y es un vector de m,

mesh(x,y,Z,C)

describe una superficie de malla con vértices de color C(i,j), situados en los puntos

(x(j), y(i), Z(i,j))

donde x corresponde a las columnas de Z e y con sus filas.

En términos más generales, si X, Y, Z y C son matrices de las mismas dimensiones,

mesh(X,Y,Z,C)

describe una superficie de malla con vértices de color C(i,j), situados en los puntos

(X(i,j), Y(i,j), Z(i,j))

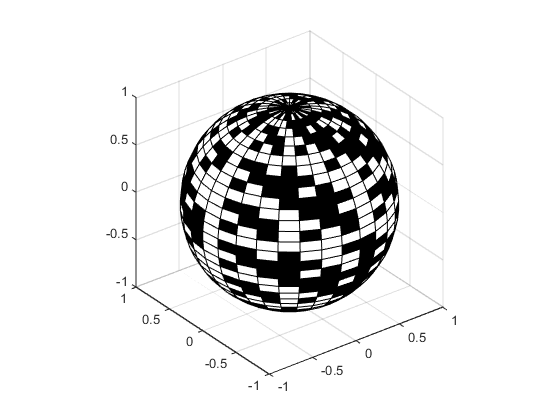
Este ejemplo usa coordenadas esféricas para dibujar una esfera y colorearla con el patrón de más y menos de una matriz de Hadamard, una matriz ortogonal utilizada en la teoría de codificación del procesamiento de señales. Los vectores theta y phi están en el intervalo -π ≤ theta ≤ π y -π/2 ≤ phi ≤ π/2. Dado que theta es un vector fila y phi es un vector columna, las multiplicaciones que producen las matrices X, Y y Z son productos vectoriales externos.

figure
k = 5;
n = 2^k-1;
theta = pi*(-n:2:n)/n;
phi = (pi/2)*(-n:2:n)'/n;
X = cos(phi)*cos(theta);
Y = cos(phi)*sin(theta);
Z = sin(phi)*ones(size(theta));
colormap([0 0 0;1 1 1])
C = hadamard(2^k); 
surf(X,Y,Z,C)
axis square

X	Y	Z
1	1	152
2	1	89
3	1	100
4	1	100
5	1	100
1	2	103
2	2	0
3	2	100
4	2	100
5	2	100
1	3	89
2	3	13
3	3	100
4	3	100
5	3	100
1	4	115
2	4	100
3	4	187
4	4	200
5	4	111
1	5	100
2	5	85
3	5	111
4	5	97
5	5	48

X	Y	Z
1	1	152
2	1	89
3	1	100
4	1	100
5	1	100
1	2	103
2	2	0
3	2	100
4	2	100
5	2	100
1	3	89
2	3	13
3	3	100
4	3	100
5	3	100
1	4	115
2	4	100
3	4	187
4	4	200
5	4	111
1	5	100
2	5	85
3	5	111
4	5	97
5	5	48

X	Y	Z
1	1	152
2	1	89
3	1	100
4	1	100
5	1	100
1	2	103
2	2	0
3	2	100
4	2	100
5	2	100
1	3	89
2	3	13
3	3	100
4	3	100
5	3	100
1	4	115
2	4	100
3	4	187
4	4	200
5	4	111
1	5	100
2	5	85
3	5	111
4	5	97
5	5	48