Calcular los pares motores de las articulaciones para equilibrar una fuerza y momento de punto final

Abrir script en vivo

Generar pares motor para equilibrar una fuerza de punto final que actúa sobre el cuerpo del efector final de un robot plano. Para calcular los pares motor de las articulaciones con diversos métodos, utilice las funciones de objeto geometricJacobian y inverseDynamics para un modelo de robot rigidBodyTree.

Inicializar el robot

El robot twoJointRigidBodyTree es un robot plano 2D. Las configuraciones de articulaciones se generan como vectores columna.

twoJointRobot = twoJointRigidBodyTree("column");

Configuración del problema

La fuerza de punto final eeForce es un vector columna con una combinación de fuerza lineal y momento que actúa sobre el cuerpo del efector final ("tool"). Observe que este vector se expresa en el marco de coordenadas de la base y se muestra a continuación.

fx = 2; 
fy = 2;
fz = 0;
nx = 0;
ny = 0;
nz = 3;
eeForce = [nx;ny;nz;fx;fy;fz];
eeName = "tool";

Especifique la configuración de articulaciones del robot para los pares motor de equilibrado.

q = [pi/3;pi/4];
Tee = getTransform(twoJointRobot,q,eeName);

Método de jacobiana geométrica

Utilizando el principio del trabajo virtual [1], encuentre el par motor de equilibrado utilizando la función de objeto geometricJacobian y multiplicando la traspuesta de la jacobiana por el vector de fuerza de punto final.

J = geometricJacobian(twoJointRobot,q,eeName);
jointTorques = J' * eeForce;
fprintf("Joint torques using geometric Jacobian (Nm): [%.3g, %.3g]",jointTorques);

Joint torques using geometric Jacobian (Nm): [1.41, 1.78]

Dinámica inversa para una fuerza transformada espacialmente

Con otro método, calcule el par motor de equilibrado calculando la dinámica inversa con la fuerza de punto final transformada espacialmente al marco base.

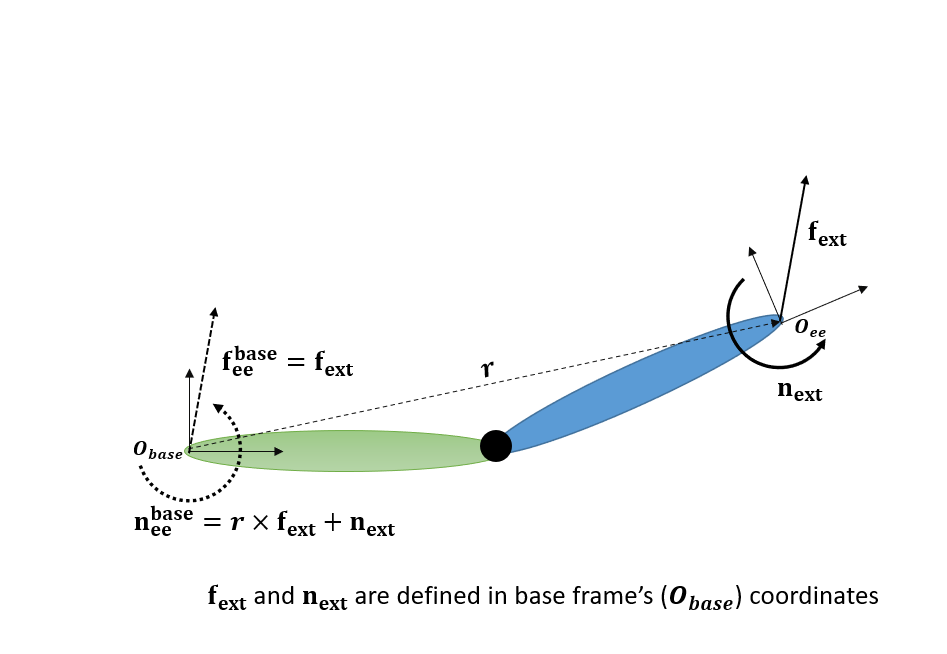
Transformar espacialmente una fuerza desde el marco del efector final al marco base significa ejercer presión sobre una nueva fuerza en un marco que resulta estar situado junto al marco base en el espacio, pero que sigue fijado al cuerpo del efector final; esta nueva fuerza tiene el mismo efecto que la fuerza original sobre la que se ejerció presión en el origen de ee. En la figura siguiente, $f_{ext}$ y $n_{ext}$ son la fuerza y el momento lineales de punto final, respectivamente, y $f_{ee}^{base}$ y $n_{ee}^{base}$ son las fuerzas y los momentos transformados espacialmente, respectivamente. En el fragmento siguiente, fbase_ee es la fuerza transformada espacialmente.

r = tform2trvec(Tee);
fbase_ee = [cross(r,[fx fy fz])' + [nx;ny;nz]; fx;fy;fz];
fext = -externalForce(twoJointRobot, eeName, fbase_ee);
jointTorques2 = inverseDynamics(twoJointRobot, q, [], [], fext);
fprintf("Joint torques using inverse dynamics (Nm): [%.3g, %.3g]",jointTorques2)

Joint torques using inverse dynamics (Nm): [1.41, 1.78]

Dinámica inversa para la fuerza del efector final

En lugar de transformar espacialmente la fuerza de punto final al marco base, utilice un tercer método expresando la fuerza del efector final en su propio marco de coordenadas (fee_ee). Transforme los vectores de momento y fuerza lineal en el marco de coordenadas del efector final. Luego, especifique esa fuerza y la configuración actual para la función externalForce. Calcule la dinámica inversa a partir de este vector de fuerza.

eeLinearForce = Tee \ [fx;fy;fz;0];
eeMoment = Tee \ [nx;ny;nz;0];
fee_ee = [eeMoment(1:3); eeLinearForce(1:3)];
fext = -externalForce(twoJointRobot,eeName,fee_ee,q);
jointTorques3 = inverseDynamics(twoJointRobot, q, [], [], fext);
fprintf("Joint torques using inverse dynamics (Nm): [%.3g, %.3g]",jointTorques3);

Joint torques using inverse dynamics (Nm): [1.41, 1.78]

Referencias

[1]Siciliano, B., Sciavicco, L., Villani, L., & Oriolo, G. (2009). Differential kinematics and statics. Robotics: Modelling, Planning and Control, 105-160.

[2]Harry Asada, and John Leonard. 2.12 Introduction to Robotics. Fall 2005. Capítulo 6 Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. Licencia: Creative Commons BY-NC-SA.