peig
Pseudospectrum using eigenvector method
Syntax
Description
[
implements the eigenvector spectral estimation method and returns S,wo] = peig(x,p)S,
the pseudospectrum estimate of the input signal x, and a vector
wo of normalized frequencies (in rad/sample) at which the
pseudospectrum is evaluated. The pseudospectrum is calculated using estimates of the
eigenvectors of a correlation matrix associated with the input data
x. You can specify the signal subspace dimension using the input
argument p.
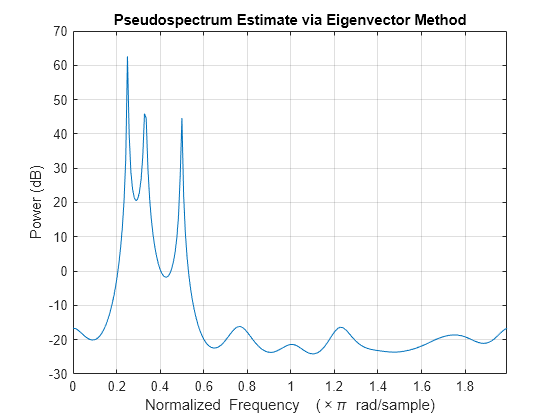
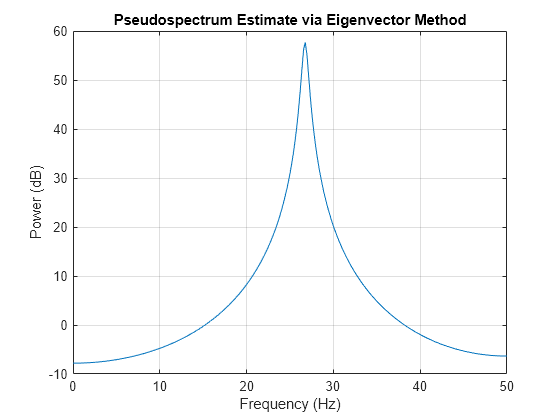
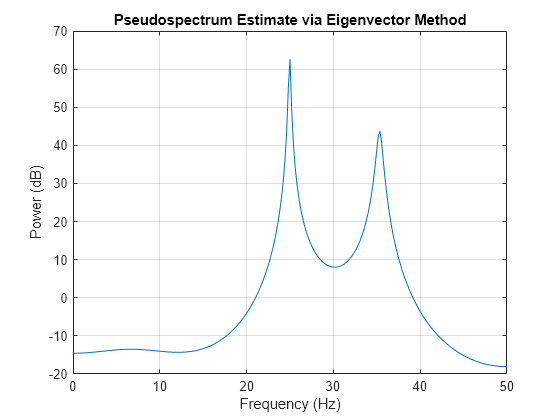
peig(___) with no output arguments plots the
pseudospectrum in the current figure window.
Examples
Input Arguments
Output Arguments
Algorithms
The eigenvector method estimates the pseudospectrum from a signal or a correlation matrix
using a weighted version of the MUSIC algorithm derived from Schmidt's eigenspace analysis
method [1]
[2]. The algorithm performs
eigenspace analysis of the signal's correlation matrix to estimate the signal's frequency
content. If you do not supply the correlation matrix, the eigenvalues and eigenvectors of the
signal's correlation matrix are estimated using svd. This algorithm is particularly suitable for signals that are the sum of
sinusoids with additive white Gaussian noise.
The eigenvector method produces a pseudospectrum estimate given by
where N is the dimension of the eigenvectors and vkis the kth eigenvector of the correlation matrix of the input signal. The integer p is the dimension of the signal subspace, so the eigenvectors vk used in the sum correspond to the smallest eigenvalues λk of the correlation matrix. The eigenvectors used span the noise subspace. The vector e(f) consists of complex exponentials, so the inner product vkHe(f) amounts to a Fourier transform. This is used for computation of the pseudospectrum. The FFT is computed for each vk and then the squared magnitudes are summed and scaled.
References
[1] Marple, S. Lawrence. Digital Spectral Analysis. Englewood Cliffs, NJ: Prentice-Hall, 1987, pp. 373–378.
[2] Schmidt, R. O. “Multiple Emitter Location and Signal Parameter Estimation.” IEEE® Transactions on Antennas and Propagation. Vol. AP-34, March, 1986, pp. 276–280.
[3] Stoica, Petre, and Randolph L. Moses. Spectral Analysis of Signals. Upper Saddle River, NJ: Prentice Hall, 2005.
Extended Capabilities
Version History
Introduced before R2006a