Extended Kalman Filter
Estimate states of discrete-time nonlinear system using extended Kalman filter
Libraries:
Control System Toolbox /
State Estimation
System Identification Toolbox /
Estimators
Description
The Extended Kalman Filter block estimates the states of a discrete-time nonlinear system using the first-order discrete-time extended Kalman filter algorithm.
Consider a plant with states x, input u, output y, process noise w, and measurement noise v. Assume that you can represent the plant as a nonlinear system.

Using the state transition and measurement functions of the system and the extended Kalman filter algorithm, the block produces state estimates for the current time step. For information about the algorithm, see Extended and Unscented Kalman Filter Algorithms for Online State Estimation.
You create the nonlinear state transition function and measurement functions for the system and specify these functions in the block. The block supports state estimation of a system with multiple sensors that are operating at different sampling rates. You can specify up to five measurement functions, each corresponding to a sensor in the system. You can also specify the Jacobians of the state transition and measurement functions. If you do not specify them, the software numerically computes the Jacobians. For more information, see State Transition and Measurement Functions.
Examples
Estimate States of Nonlinear System with Multiple, Multirate Sensors
Use an Extended Kalman Filter block to estimate the states of a system with multiple sensors that are operating at different sampling rates.
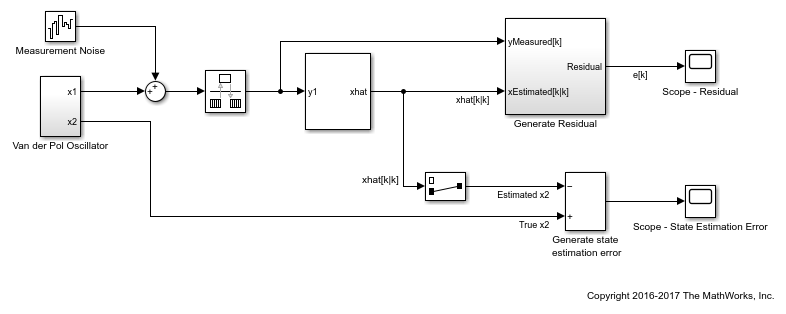
Compute Residuals and State Estimation Errors
Estimate the states of a discrete-time Van der Pol oscillator and compute state estimation errors and residuals for validating the estimation. The residuals are the output estimation errors, that is, they are the difference between the measured and estimated outputs.
Nonlinear State Estimation of a Degrading Battery System
Estimate the states of a nonlinear system using an unscented Kalman filter in Simulink®.
Ports
Input
Measured system outputs corresponding to each measurement function that you specify in the block. The number of ports equals the number of measurement functions in your system. You can specify up to five measurement functions. For example, if your system has two sensors, you specify two measurement functions in the block. The first port y1 is available by default. When you click Apply, the software generates port y2 corresponding to the second measurement function.
Specify the ports as N-dimensional vectors, where N is the number of quantities measured by the corresponding sensor. For example, if your system has one sensor that measures the position and velocity of an object, then there is only one port y1. The port is specified as a 2-dimensional vector with values corresponding to position and velocity.
Dependencies
The first port y1 is available by default. Ports y2 to y5 are generated when you click Add Measurement, and click Apply.
Data Types: single | double
Additional optional input argument to the state transition function
f other than the state x and
process noise w. For information about state
transition functions see, State Transition and Measurement Functions.
Suppose that your system has nonadditive process noise, and the state
transition function f has the following form:
x(k+1) =
f(x(k),w(k),StateTransitionFcnInputs)
Here k is the time step, and
StateTransitionFcnInputs is an additional input
argument other than x and
w.
If you create f using a MATLAB® function (.m file), the software
generates the port StateTransitionFcnInputs when
you click Apply. You can specify the inputs to
this port as a scalar, vector, or matrix.
If your state transition function has more than one additional input, use a Simulink Function (Simulink) block to specify the function. When you use a Simulink Function block, you provide the additional inputs directly to the Simulink Function block using Inport (Simulink) blocks. No input ports are generated for the additional inputs in the Extended Kalman Filter block. For an example, see Online State Estimation Using Identified Nonlinear Models (System Identification Toolbox).
Dependencies
This port is generated only if both of the following conditions are satisfied:
You specify
fin Function using a MATLAB function, andfis on the MATLAB path.frequires only one additional input argument apart fromxandw.
Data Types: single | double
Additional optional inputs to the measurement functions other than the
state x and measurement noise v.
For information about measurement functions see, State Transition and Measurement Functions.
MeasurementFcn1Inputs corresponds to the first
measurement function that you specify, and so on. For example, suppose
that your system has three sensors and nonadditive measurement noise,
and the three measurement functions h1,
h2, and h3 have the following
form:
y1[k] = h1(x[k],v1[k],MeasurementFcn1Inputs)
y2[k] = h2(x[k],v2[k],MeasurementFcn2Inputs)
y3[k] = h3(x[k],v3[k])
Here k is the time step, and
MeasurementFcn1Inputs and
MeasurementFcn2Inputs are the additional input
arguments to h1 and h2.
If you specify h1, h2, and
h3 using MATLAB functions (.m files) in
Function, the software generates ports
MeasurementFcn1Inputs and
MeasurementFcn2Inputs when you click
Apply. You can specify the inputs to these
ports as scalars, vectors, or matrices.
If your measurement functions have more than one additional input, use Simulink Function (Simulink) blocks to specify the functions. When you use a Simulink Function block, you provide the additional inputs directly to the Simulink Function block using Inport (Simulink) blocks. No input ports are generated for the additional inputs in the Extended Kalman Filter block. For an example, see Online State Estimation Using Identified Nonlinear Models (System Identification Toolbox).
Dependencies
A port corresponding to a measurement function
h is generated only if both of the following
conditions are satisfied:
You specify
hin Function using a MATLAB function, andhis on the MATLAB path.hrequires only one additional input argument apart fromxandv.
Data Types: single | double
Time-varying process noise covariance, specified as a scalar, vector, or matrix depending on the value of the Process noise parameter:
Process noise is
Additive— Specify the covariance as a scalar, an Ns-element vector, or an Ns-by-Ns matrix, where Ns is the number of states of the system. Specify a scalar if there is no cross-correlation between process noise terms, and all the terms have the same variance. Specify a vector of length Ns, if there is no cross-correlation between process noise terms, but all the terms have different variances.Process noise is
Nonadditive— Specify the covariance as a W-by-W matrix, where W is the number of process noise terms in the state transition function.
Dependencies
This port is generated if you specify the process noise covariance as Time-Varying. The port appears when you click Apply.
Data Types: single | double
Time-varying measurement noise covariances for up to five measurement functions of the system, specified as matrices. The sizes of the matrices depend on the value of the Measurement noise parameter for the corresponding measurement function:
Measurement noise is
Additive— Specify the covariance as an N-by-N matrix, where N is the number of measurements of the system.Measurement noise is
Nonadditive— Specify the covariance as a V-by-V matrix, where V is the number of measurement noise terms in the corresponding measurement function.
Dependencies
A port is generated if you specify the measurement noise covariance as Time-Varying for the corresponding measurement function. The port appears when you click Apply.
Data Types: single | double
Suppose that measured output data is not available at all time
points at the port y1 that corresponds to the
first measurement function. Use a signal value other than 0 at
the Enable1 port to enable the correction of
estimated states when measured data is available. Specify the port
value as 0 when measured data is not available.
Similarly, if measured output data is not available at all time points
at the port yi for
the ith measurement
function, specify the corresponding port Enablei as
a value other than 0.
Dependencies
A port corresponding to a measurement function is generated if you select Add Enable port for that measurement function. The port appears when you click Apply.
Data Types: single | double | Boolean
Output
Estimated states, returned as a vector of size Ns, where Ns is the number of states of the system. To access the individual states, use the Selector (Simulink) block.
When the Use the current measurements to improve state
estimates parameter is selected, the block outputs the
corrected state estimate at
time step k, estimated using measured outputs until
time k. If you clear this parameter, the block
returns the predicted state estimate for
time k, estimated using measured output until a
previous time k-1. Clear this parameter if your
filter is in a feedback loop and there is an algebraic loop in your Simulink model.
Data Types: single | double
State estimation error covariance, returned as an Ns-by-Ns matrix, where Ns is the number of states of the system. To access the individual covariances, use the Selector (Simulink) block.
Dependencies
This port is generated if you select Output state estimation error covariance in the System Model tab, and click Apply.
Data Types: single | double
Parameters
System Model Tab
State Transition
The state transition function calculates the
Ns-element state vector of the system at time step
k+1, given the state vector at time step
k. Ns is the number of states
of the nonlinear system. You create the state transition function and
specify the function name in Function. For example,
if vdpStateFcn.m is the state transition function
that you created and saved, specify Function as
vdpStateFcn.
The inputs to the function you create depend on whether you specify the process noise as additive or nonadditive in Process noise.
Process noise is
Additive— The state transition function f specifies how the states evolve as a function of state values at previous time step:x(k+1) = f(x(k),Us1(k),...,Usn(k)),where
x(k)is the estimated state at timek, andUs1,...,Usnare any additional input arguments required by your state transition function, such as system inputs or the sample time. To see an example of a state transition function with additive process noise, typeedit vdpStateFcnat the command line.Process noise is
Nonadditive— The state transition function also specifies how the states evolve as a function of the process noisew:x(k+1) = f(x(k),w(k),Us1(k),...,Usn(k)).
For more information, see State Transition and Measurement Functions.
You can create f using a Simulink Function (Simulink) block or
as a MATLAB function (.m file).
You can use a MATLAB function only if f has one additional input argument
Us1other thanxandw.x(k+1) = f(x(k),w(k),Us1(k))The software generates an additional input port StateTransitionFcnInputs to specify this argument.
If you are using a Simulink Function block, specify
xandwusing Argument Inport (Simulink) blocks and the additional inputsUs1,...,Usnusing Inport (Simulink) blocks in the Simulink Function block. The Argument name parameter of the Argument Inport (Simulink) and Argument Outport (Simulink) blocks in the Simulink Function block must be different from each other. You do not provideUs1,...,Usnto the Extended Kalman Filter block. For an example, see Online State Estimation Using Identified Nonlinear Models (System Identification Toolbox).
Programmatic Use
Block Parameter:
StateTransitionFcn |
| Type: character vector, string |
Default:
'myStateTransitionFcn' |
Jacobian of state transition function f, specified as one of the following:
off— The software computes the Jacobian numerically. This computation may increase processing time and numerical inaccuracy of the state estimation.on— You create a function to compute the Jacobian, and specify the name of the function in Jacobian. For example, ifvdpStateJacobianFcn.mis the Jacobian function, specify Jacobian asvdpStateJacobianFcn. If you create the state transition function f using a Simulink Function (Simulink) block, then create the Jacobian using a Simulink Function block. If you create f using a MATLAB function (.mfile), then create the Jacobian using a MATLAB function.The function calculates the partial derivatives of the state transition function with respect to the states and process noise. The number of inputs to the Jacobian function must equal the number of inputs of the state transition function and must be specified in the same order in both functions. The number of outputs of the Jacobian function depends on the Process noise parameter:
Process noise is
Additive— The function calculates the partial derivative of the state transition function f with respect to the states (). The output is an Ns-by-Ns Jacobian matrix, where Ns is the number of states.To see an example of a Jacobian function for additive process noise, type
edit vdpStateJacobianFcnat the command line.Process noise is
Nonadditive— The function must also return a second output that is the partial derivative of the state transition function f with respect to the process noise terms (). The second output is returned as an Ns-by-W matrix, where W is the number of process noise terms in the state transition function.
Programmatic Use
Block Parameter:
HasStateTransitionJacobianFcn |
| Type: character vector |
Values:
'off','on' |
Default:
'off' |
Block Parameter:
StateTransitionJacobianFcn |
| Type: character vector, string |
Default:
'' |
Process noise characteristics, specified as one of the following values:
Additive— Process noisewis additive, and the state transition function f that you specify in Function has the following form:x(k+1) = f(x(k),Us1(k),...,Usn(k)),where
x(k)is the estimated state at timek, andUs1,...,Usnare any additional input arguments required by your state transition function.Nonadditive— Process noise is nonadditive, and the state transition function specifies how the states evolve as a function of the state and process noise at the previous time step:x(k+1) = f(x(k),w(k),Us1(k),...,Usn(k)).
Programmatic Use
Block Parameter: HasAdditiveProcessNoise |
| Type: character vector |
Values: 'Additive', 'Nonadditive' |
Default: 'Additive' |
Time-invariant process noise covariance, specified as a scalar, vector, or matrix depending on the value of the Process noise parameter:
Process noise is
Additive— Specify the covariance as a scalar, an Ns-element vector, or an Ns-by-Ns matrix, where Ns is the number of states of the system. Specify a scalar if there is no cross-correlation between process noise terms and all the terms have the same variance. Specify a vector of length Ns, if there is no cross-correlation between process noise terms but all the terms have different variances.Process noise is
Nonadditive— Specify the covariance as a W-by-W matrix, where W is the number of process noise terms.
If the process noise covariance is time-varying, select Time-varying. The block generates input port Q to specify the time-varying covariance.
Dependencies
This parameter is enabled if you do not specify the process noise as Time-Varying.
Programmatic Use
Block Parameter: ProcessNoise |
| Type: character vector, string |
Default: '1' |
If you select this parameter, the block includes an additional input port Q to specify the time-varying process noise covariance.
Programmatic Use
Block Parameter: HasTimeVaryingProcessNoise |
| Type: character vector |
Values: 'off', 'on' |
Default: 'off' |
Initialization
Initial state estimate value, specified as an Ns-element vector, where Ns is the number of states in the system. Specify the initial state values based on your knowledge of the system.
Programmatic Use
Block Parameter: InitialState |
| Type: character vector, string |
Default: '0' |
State estimation error covariance, specified as a scalar, an Ns-element vector, or an Ns-by-Ns matrix, where Ns is the number of states of the system. If you specify a scalar or vector, the software creates an Ns-by-Ns diagonal matrix with the scalar or vector elements on the diagonal.
Specify a high value for the covariance when you do not have confidence in the initial state values that you specify in Initial state.
Programmatic Use
Block Parameter: InitialStateCovariance |
| Type: character vector, string |
Default: '1' |
Measurement
The measurement function calculates the N-element
output measurement vector of the nonlinear system at time step
k, given the state vector at time step
k. You create the measurement function and
specify the function name in Function. For example,
if vdpMeasurementFcn.m is the measurement function
that you created and saved, specify Function as
vdpMeasurementFcn.
The inputs to the function you create depend on whether you specify the measurement noise as additive or nonadditive in Measurement noise.
Measurement noise is
Additive— The measurement function h specifies how the measurements evolve as a function of state Values:y(k) = h(x(k),Um1(k),...,Umn(k)),where
y(k)andx(k)are the estimated output and estimated state at timek, andUm1,...,Umnare any optional input arguments required by your measurement function. For example, if you are using a sensor for tracking an object, an additional input could be the sensor position.To see an example of a measurement function with additive process noise, type
edit vdpMeasurementFcnat the command line.Measurement noise is
Nonadditive— The measurement function also specifies how the output measurement evolves as a function of the measurement noisev:y(k) = h(x(k),v(k),Um1(k),...,Umn(k)).To see an example of a measurement function with nonadditive process noise, type
edit vdpMeasurementNonAdditiveNoiseFcn.
For more information, see State Transition and Measurement Functions.
You can create h using a Simulink Function (Simulink) block or
as a MATLAB function (.m file).
You can use a MATLAB function only if h has one additional input argument
Um1other thanxandv.y[k] = h(x[k],v[k],Um1(k))The software generates an additional input port MeasurementFcn
iInputs to specify this argument for the ith measurement function.If you are using a Simulink Function block, specify
xandvusing Argument Inport (Simulink) blocks and the additional inputsUm1,...,Umnusing Inport (Simulink) blocks in the Simulink Function block. The Argument name parameter of the Argument Inport (Simulink) and Argument Outport (Simulink) blocks in the Simulink Function block must be different from each other. You do not provideUm1,...,Umnto the Extended Kalman Filter block. For an example, see Online State Estimation Using Identified Nonlinear Models (System Identification Toolbox).
If you have multiple sensors in your system, you can specify multiple measurement functions. You can specify up to five measurement functions using the Add Measurement button. To remove measurement functions, use Remove Measurement.
Programmatic Use
Block Parameter:
MeasurementFcn1,
MeasurementFcn2,
MeasurementFcn3,
MeasurementFcn4,
MeasurementFcn5 |
| Type: character vector, string |
Default:
'myMeasurementFcn' |
Jacobian of measurement function h, specified as one of the following:
off— The software computes the Jacobian numerically. This computation may increase processing time and numerical inaccuracy of the state estimation.on— You create a function to compute the Jacobian of the measurement function h, and specify the name of the function in Jacobian. For example, ifvdpMeasurementJacobianFcn.mis the Jacobian function, specifyMeasurementJacobianFcnasvdpMeasurementJacobianFcn. If you create h using a Simulink Function (Simulink) block, then create the Jacobian using a Simulink Function block. If you create h using a MATLAB function (.mfile), then create the Jacobian using a MATLAB function.The function calculates the partial derivatives of the measurement function h with respect to the states and measurement noise. The number of inputs to the Jacobian function must equal the number of inputs to the measurement function and must be specified in the same order in both functions. The number of outputs of the Jacobian function depends on the Measurement noise parameter:
Measurement noise is
Additive— The function calculates the partial derivatives of the measurement function with respect to the states (). The output is as an N-by-Ns Jacobian matrix, where N is the number of measurements of the system and Ns is the number of states.To see an example of a Jacobian function for additive measurement noise, type
edit vdpMeasurementJacobianFcnat the command line.Measurement noise is
Nonadditive— The function also returns a second output that is the partial derivative of the measurement function with respect to the measurement noise terms (). The second output is returned as an N-by-V Jacobian matrix, where V is the number of measurement noise terms.
Programmatic Use
Block Parameter:
HasMeasurementJacobianFcn1,
HasMeasurementJacobianFcn2,
HasMeasurementJacobianFcn3,
HasMeasurementJacobianFcn4,HasMeasurementJacobianFcn5 |
| Type: character vector |
Values:
'off','on' |
Default:
'off' |
Block Parameter:
MeasurementJacobianFcn1,
MeasurementJacobianFcn2,
MeasurementJacobianFcn3,
MeasurementJacobianFcn4,
MeasurementJacobianFcn5 |
| Type: character vector |
Default:
'' |
Measurement noise characteristics, specified as one of the following values:
Additive— Measurement noisevis additive, and the measurement function h that you specify in Function has the following form:y(k) = h(x(k),Um1(k),...,Umn(k)),where
y(k)andx(k)are the estimated output and estimated state at timek, andUm1,...,Umnare any optional input arguments required by your measurement function.Nonadditive— Measurement noise is nonadditive, and the measurement function specifies how the output measurement evolves as a function of the state and measurement noise:y(k) = h(x(k),v(k),Um1(k),...,Umn(k)).
Programmatic Use
Block Parameter: HasAdditiveMeasurementNoise1, HasAdditiveMeasurementNoise2, HasAdditiveMeasurementNoise3, HasAdditiveMeasurementNoise4, HasAdditiveMeasurementNoise5 |
| Type: character vector |
Values: 'Additive', 'Nonadditive' |
Default: 'Additive' |
Select this parameter to enable measurement wrapping to estimate states when you have circular measurements that are independent of your model states. If you select this parameter, then the measurement function you specify must include the following two outputs:
The measurement, specified as a N-element output measurement vector of the nonlinear system at time step k, given the state vector at time step k. N is the number of measurements of the system.
The measurement wrapping bounds, specified as an N-by-
2matrix where, the first column provides the minimum measurement bound and the second column provides the maximum measurement bound.
Enabling the Enable measurement wrapping check box wraps the measurement residuals in a defined bound, which helps to prevent the filter from divergence due to incorrect measurement residual values. For an example, see State Estimation with Wrapped Measurements Using Extended Kalman Filter.
Programmatic Use
Block Parameter:
EnableMeasurementWrapping1,
EnableMeasurementWrapping2,
EnableMeasurementWrapping3,
EnableMeasurementWrapping4,
EnableMeasurementWrapping5 |
| Type: character vector |
Values: 'off',
'on' |
Default: 'off' |
Time-invariant process noise covariance, specified as a scalar, vector, or matrix depending on the value of the Process noise parameter:
Process noise is
Additive— Specify the covariance as a scalar, an Ns-element vector, or an Ns-by-Ns matrix, where Ns is the number of states of the system. Specify a scalar if there is no cross-correlation between process noise terms and all the terms have the same variance. Specify a vector of length Ns, if there is no cross-correlation between process noise terms but all the terms have different variances.Process noise is
Nonadditive— Specify the covariance as a W-by-W matrix, where W is the number of process noise terms.
If the process noise covariance is time-varying, select Time-varying. The block generates input port Q to specify the time-varying covariance.
Dependencies
This parameter is enabled if you do not specify the process noise as Time-Varying.
Programmatic Use
Block Parameter:
ProcessNoise |
| Type: character vector, string |
Default:
'1' |
If you select this parameter for the measurement noise covariance of
the first measurement function, the block includes an additional input
port R1. You specify the time-varying measurement
noise covariance in R1. Similarly, if you select
Time-varying for the
ith measurement
function, the block includes an additional input port
Ri to specify
the time-varying measurement noise covariance for that function.
Programmatic Use
Block Parameter:
HasTimeVaryingMeasurementNoise1,
HasTimeVaryingMeasurementNoise2,
HasTimeVaryingMeasurementNoise3,
HasTimeVaryingMeasurementNoise4,
HasTimeVaryingMeasurementNoise5 |
| Type: character vector |
Values:
'off',
'on' |
Default:
'off' |
Suppose that measured output data is not available at all time
points at the port y1 that corresponds to the
first measurement function. Select Add Enable port to
generate an input port Enable1. Use a signal
at this port to enable the correction of estimated states only when
measured data is available. Similarly, if measured output data is
not available at all time points at the port yi for
the ith measurement
function, select the corresponding Add Enable port.
Programmatic Use
Block Parameter: HasMeasurementEnablePort1, HasMeasurementEnablePort2, HasMeasurementEnablePort3, HasMeasurementEnablePort4, HasMeasurementEnablePort5 |
| Type: character vector |
Values: 'off', 'on' |
Default: 'off' |
Settings
When this parameter is selected, the block outputs the corrected
state estimate at
time step k, estimated using measured outputs until
time k. If you clear this parameter, the block
returns the predicted state estimate for
time k, estimated using measured output until a
previous time k-1. Clear this parameter if your
filter is in a feedback loop and there is an algebraic loop in your Simulink model.
Programmatic Use
Block Parameter: UseCurrentEstimator |
| Type: character vector |
Values: 'off', 'on' |
Default: 'on' |
If you select this parameter, a state estimation error covariance output port P is generated in the block.
Programmatic Use
Block Parameter:
OutputStateCovariance |
| Type: character vector |
Values:
'off','on' |
Default: 'off' |
Use this parameter to specify the data type for all block parameters.
Programmatic Use
Block Parameter: DataType |
| Type: character vector |
Values: 'single', 'double' |
Default: 'double' |
Block sample time, specified as a positive scalar. If the sample times of your state transition and measurement functions are different, select Enable multirate operation in the Multirate tab, and specify the sample times in the Multirate tab instead.
Dependencies
This parameter is available if in the Multirate tab,
the Enable multirate operation parameter is off.
Programmatic Use
Block Parameter: SampleTime |
| Type: character vector, string |
Default: '1' |
Multirate Tab
Select this parameter if the sample times of the state transition and measurement functions are different. You specify the sample times in the Multirate tab, in Sample time.
Programmatic Use
Block Parameter: EnableMultirate |
| Type: character vector |
Values: 'off', 'on' |
Default: 'off' |
If the sample times for state transition and measurement functions are different, specify Sample time. Specify the sample times for the measurement functions as positive integer multiples of the state transition sample time. The sample times you specify correspond to the following input ports:
Ports corresponding to state transition function — Additional input to state transition function StateTransitionFcnInputs and time-varying process noise covariance Q. The sample times of these ports must always equal the state transition function sample time, but can differ from the sample time of the measurement functions.
Ports corresponding to ith measurement function — Measured output y
i, additional input to measurement function MeasurementFcniInputs, enable signal at port Enablei, and time-varying measurement noise covariance Ri. The sample times of these ports for the same measurement function must always be the same, but can differ from the sample time for the state transition function and other measurement functions.
Dependencies
This parameter is available if in the Multirate tab, the
Enable multirate operation parameter is
on.
Programmatic Use
Block Parameter:
StateTransitionFcnSampleTime,
MeasurementFcn1SampleTime1,
MeasurementFcn1SampleTime2,
MeasurementFcn1SampleTime3,
MeasurementFcn1SampleTime4,
MeasurementFcn1SampleTime5 |
| Type: character vector, string |
Default: '1' |
More About
The algorithm computes the state estimates of the nonlinear system using state transition and measurement functions specified by you. You can specify up to five measurement functions, each corresponding to a sensor in the system. The software lets you specify the noise in these functions as additive or nonadditive.
Additive Noise Terms — The state transition and measurements equations have the following form:
Here f is a nonlinear state transition function that describes the evolution of states
xfrom one time step to the next. The nonlinear measurement function h relatesxto the measurementsyat time stepk.wandvare the zero-mean, uncorrelated process and measurement noises, respectively. These functions can also have additional optional input arguments that are denoted byusandumin the equations. For example, the additional arguments could be time stepkor the inputsuto the nonlinear system. There can be multiple such arguments.Note that the noise terms in both equations are additive. That is,
x(k+1)is linearly related to the process noisew(k), andy(k)is linearly related to the measurement noisev(k). For additive noise terms, you do not need to specify the noise terms in the state transition and measurement functions. The software adds the terms to the output of the functions.Nonadditive Noise Terms — The software also supports more complex state transition and measurement functions where the state x[k] and measurement y[k] are nonlinear functions of the process noise and measurement noise, respectively. When the noise terms are nonadditive, the state transition and measurements equation have the following form:
Extended Capabilities
The state transition, measurement, and Jacobian functions that you specify must use only the MATLAB commands and Simulink blocks that support code generation. For a list of blocks that support code generation, see Blocks Supported for Code Generation (Simulink Coder). For a list of commands that support code generation, see Functions and Objects Supported for C/C++ Code Generation (MATLAB Coder).
Generated code uses an algorithm that is different from the algorithm that the Extended Kalman Filter block itself uses. You might see some numerical differences in the results obtained using the two methods.
Version History
Introduced in R2017aStarting in R2020b, numerical improvements in the Extended Kalman Filter algorithm might produce results that are different from the results you obtained in previous versions.
See Also
Blocks
Functions
Topics
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)