Esta página se ha traducido mediante traducción automática. Haga clic aquí para ver la última versión en inglés.

ga

Encontrar el mínimo de una función mediante un algoritmo genético

Sintaxis

x = ga(fun,nvars)

x = ga(fun,nvars,A,b)

x = ga(fun,nvars,A,b,Aeq,beq)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon,options)

x = ga(problem)

[x,fval] = ga(___)

[x,fval,exitflag,output] = ga(___)

[x,fval,exitflag,output,population,scores] = ga(___)

Descripción

x = ga(fun,nvars) encuentra un mínimo local sin restricciones, x, para la función objetivo, fun. nvars es la dimensión (número de variables de diseño) de fun.

Nota

En Pasar parámetros adicionales se explica cómo pasar parámetros adicionales a la función objetivo y a las funciones de restricción no lineales, si fuera necesario.

x = ga(fun,nvars,A,b) encuentra un mínimo local x para fun, sujeto a las desigualdades lineales A*x ≤ b . ga evalúa el producto matricial A*x como si x estuviera transpuesto (A*x').

x = ga(fun,nvars,A,b,Aeq,beq) encuentra un mínimo local x para fun, sujeto a las igualdades lineales Aeq*x = beq y A*x ≤ b . (Establezca A=[] y b=[] si no existen desigualdades lineales). ga evalúa el producto matricial Aeq*x como si x estuviera transpuesto (Aeq*x').

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub) define un conjunto de límites inferior y superior en las variables de diseño, x, de modo que se encuentre una solución en el rango lb ≤ x ≤ ub. (Establezca Aeq=[] y beq=[] si no existen igualdades lineales).

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon) somete la minimización a las restricciones definidas en nonlcon. La función nonlcon acepta x y devuelve los vectores C y Ceq, que representan las desigualdades e igualdades no lineales respectivamente. ga minimiza fun de modo que C(x) ≤ 0 y Ceq(x) = 0. (Establezca lb=[] y ub=[] si no existen límites).

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options) se minimiza con los parámetros de optimización predeterminados reemplazados por valores en options. (Establezca nonlcon=[] si no existen restricciones no lineales). Cree options utilizando optimoptions.

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon) o x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon,options) requiere que las variables enumeradas en intcon tomen valores enteros.

Nota

Cuando hay restricciones de números enteros, ga no acepta restricciones de igualdad no lineal, solo restricciones de desigualdad no lineal.

x = ga(problem) encuentra el mínimo para problem, una estructura descrita en problem.

[x,fval] = ga(___), para cualquier argumento de entrada anterior, también devuelve fval, el valor de la función de aptitud en x.

[x,fval,exitflag,output] = ga(___) también devuelve exitflag, un entero que identifica el motivo por el cual finalizó el algoritmo, y output, una estructura que contiene la salida de cada generación y otra información sobre el rendimiento del algoritmo.

[x,fval,exitflag,output,population,scores] = ga(___) también devuelve una matriz population, cuyas filas son la población final, y un vector scores, las puntuaciones de la población final.

Ejemplos

Optimizar una función no suave usando ga

El archivo ps_example.m se incluye cuando ejecuta este ejemplo. Represente la función.

xi = linspace(-6,2,300);
yi = linspace(-4,4,300);
[X,Y] = meshgrid(xi,yi);
Z = ps_example([X(:),Y(:)]);
Z = reshape(Z,size(X));
surf(X,Y,Z,'MeshStyle','none')
colormap 'jet'
view(-26,43)
xlabel('x(1)')
ylabel('x(2)')
title('ps\_example(x)')

Encuentra el mínimo de esta función usando ga .

rng default % For reproducibility
x = ga(@ps_example,2)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -4.6793   -0.0860

Minimizar una función no uniforme con restricciones lineales

Utilice el algoritmo genético para minimizar la función ps_example en la región x(1) + x(2) >= 1 y x(2) <= 5 + x(1). Esta función se incluye cuando se ejecuta este ejemplo.

Primero, convierta las dos restricciones de desigualdad a la forma matricial A*x <= b . En otras palabras, obtenga las variables x en el lado izquierdo de la desigualdad y haga que ambas desigualdades sean menores o iguales:

-x(1) -x(2) <= -1

-x(1) + x(2) <= 5

A = [-1,-1;
    -1,1];
b = [-1;5];

Resuelva el problema restringido usando ga .

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

    0.9990    0.0000

Las restricciones se satisfacen dentro del valor predeterminado de la tolerancia de restricción, 1e-3. Para ver esto, calcule A*x' - b, que debe tener componentes negativos.

disp(A*x' - b)

    0.0010
   -5.9990

Minimizar una función no uniforme con restricciones de igualdad y desigualdad lineales

Utilice el algoritmo genético para minimizar la función ps_example en la región x(1) + x(2) >= 1 y x(2) == 5 + x(1). Esta función se incluye cuando se ejecuta este ejemplo.

Primero, convierta las dos restricciones a la forma matricial A*x <= b y Aeq*x = beq. En otras palabras, obtenga las variables x en el lado izquierdo de las expresiones y convierta la desigualdad en la forma menor o igual:

-x(1) -x(2) <= -1

-x(1) + x(2) == 5

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;

Resuelva el problema restringido usando ga .

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b,Aeq,beq)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -2.0005    2.9995

Verifique que las restricciones se cumplan dentro del valor predeterminado de ConstraintTolerance, 1e-3.

disp(A*x' - b)

   1.0000e-03

disp(Aeq*x' - beq)

   8.5897e-09

Optimizar con restricciones y límites lineales

Utilice el algoritmo genético para minimizar la función ps_example en la región x(1) + x(2) >= 1 y x(2) == 5 + x(1). La función ps_example se incluye cuando ejecuta este ejemplo. Además, establezca los límites 1 <= x(1) <= 6 y -3 <= x(2) <= 8.

Primero, convierta las dos restricciones lineales a la forma matricial A*x <= b y Aeq*x = beq. En otras palabras, obtenga las variables x en el lado izquierdo de las expresiones y convierta la desigualdad en la forma menor o igual:

-x(1) -x(2) <= -1

-x(1) + x(2) == 5

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;

Establezca los límites lb y ub.

lb = [1 -3];
ub = [6 8];

Resuelva el problema restringido usando ga .

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b,Aeq,beq,lb,ub)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

    1.0000    6.0000

Verifique que las restricciones lineales se cumplan dentro del valor predeterminado de ConstraintTolerance, 1e-3.

disp(A*x' - b)

   -6.0000

disp(Aeq*x' - beq)

  -7.9765e-08

Optimizar con restricciones no lineales utilizando ga

Utilice el algoritmo genético para minimizar la función ps_example en la región $2{\mathit{x}}_1^2+{\mathit{x}}_2^2\le 3$ y $$(x_1+1{)}^2=(x_2/2{)}^4$$. La función ps_example se incluye cuando ejecuta este ejemplo.

Para ello, utilice la función ellipsecons.m que devuelve la restricción de desigualdad en la primera salida, c, y la restricción de igualdad en la segunda salida, ceq. La función ellipsecons se incluye cuando ejecuta este ejemplo. Examine el código ellipsecons.

type ellipsecons

function [c,ceq] = ellipsecons(x)

c = 2*x(1)^2 + x(2)^2 - 3;
ceq = (x(1)+1)^2 - (x(2)/2)^4;

Incluya un identificador de función para ellipsecons como argumento nonlcon.

nonlcon = @ellipsecons;
fun = @ps_example;
rng default % For reproducibility
x = ga(fun,2,[],[],[],[],[],[],nonlcon)

Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -0.9766    0.0362

Compruebe que las restricciones no lineales se satisfacen en x . Las restricciones se satisfacen cuando c ≤ 0 y ceq = 0 dentro del valor predeterminado de ConstraintTolerance, 1e-3.

[c,ceq] = nonlcon(x)

c = 
-1.0911

ceq = 
5.4645e-04

Minimizar con opciones no predeterminadas

Utilice el algoritmo genético para minimizar la función ps_example en la región x(1) + x(2) >= 1 y x(2) == 5 + x(1) utilizando una tolerancia de restricción que sea menor que la predeterminada. La función ps_example se incluye cuando ejecuta este ejemplo.

Primero, convierta las dos restricciones a la forma matricial A*x <= b y Aeq*x = beq. En otras palabras, obtenga las variables x en el lado izquierdo de las expresiones y convierta la desigualdad en la forma menor o igual:

-x(1) -x(2) <= -1

-x(1) + x(2) == 5

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;

Para obtener una solución más precisa, establezca una tolerancia de restricción de 1e-6. Y para monitorear el progreso del solucionador, configure una función de gráfico.

options = optimoptions('ga','ConstraintTolerance',1e-6,'PlotFcn', @gaplotbestf);

Resolver el problema de minimización.

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b,Aeq,beq,[],[],[],options)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

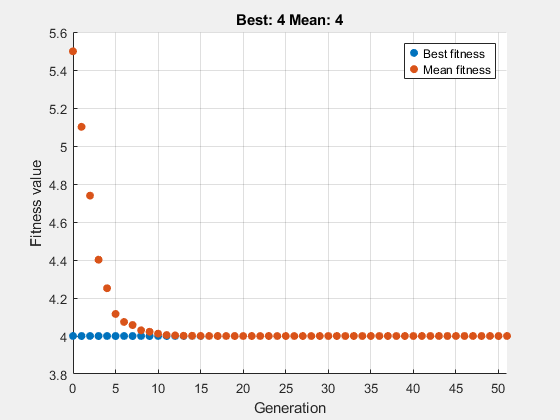
x = 1×2

   -2.0000    3.0000

Compruebe que las restricciones lineales se satisfacen dentro de 1e-6.

disp(A*x' - b)

   9.9809e-07

disp(Aeq*x' - beq)

  -7.3589e-08

Minimizar una función no lineal con restricciones de números enteros

Utilice el algoritmo genético para minimizar la función ps_example sujeta a la restricción de que x(1) es un entero. Esta función se incluye cuando se ejecuta este ejemplo.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
x = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon)

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -5.0000   -0.0834

Obtener la solución y el valor de la función

Utilice el algoritmo genético para minimizar un problema no lineal restringido a números enteros. Obtenga tanto la ubicación del mínimo como el valor mínimo de la función. La función objetivo, ps_example, se incluye cuando ejecuta este ejemplo.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
[x,fval] = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon)

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -5.0000   -0.0834

fval = 
-1.8344

Compare este resultado con la solución del problema sin restricciones.

[x,fval] = ga(fun,2)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -4.6906   -0.0078

fval = 
-1.9918

Obtener información de diagnóstico

Utilice el algoritmo genético para minimizar la función ps_example restringida a tener un valor entero x(1). La función ps_example se incluye cuando ejecuta este ejemplo. Para comprender el motivo por el cual el solucionador se detuvo y cómo ga buscó un mínimo, obtenga los resultados exitflag y output. Además, grafique el valor mínimo observado de la función objetivo a medida que avanza el solucionador.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
options = optimoptions('ga','PlotFcn', @gaplotbestf);
[x,fval,exitflag,output] = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon,options)

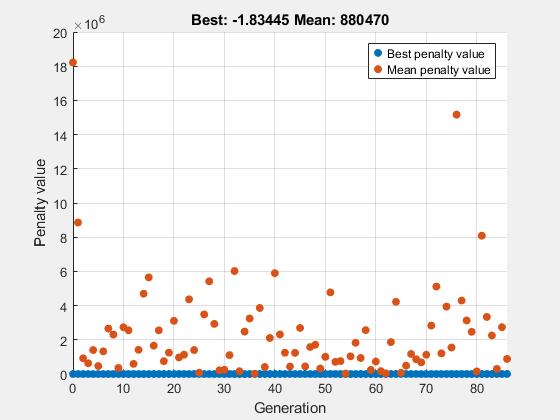
ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -5.0000   -0.0834

fval = 
-1.8344

exitflag = 
1

output = struct with fields:
      problemtype: 'integerconstraints'
         rngstate: [1x1 struct]
      generations: 86
        funccount: 3311
          message: 'ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and ...'
    maxconstraint: 0
       hybridflag: []

Obtener población y puntuaciones finales

Utilice el algoritmo genético para minimizar la función ps_example restringida a tener un valor entero x(1). La función ps_example se incluye cuando ejecuta este ejemplo. Obtenga todas las salidas, incluida la población final y el vector de puntuaciones.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
[x,fval,exitflag,output,population,scores] = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon);

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

Examine los primeros 10 miembros de la población final y sus puntuaciones correspondientes. Tenga en cuenta que x(1) tiene un valor entero para todos estos miembros de la población. El algoritmo entero ga genera únicamente poblaciones factibles para números enteros.

disp(population(1:10,:))

   1.0e+03 *

   -0.0050   -0.0001
   -0.0050   -0.0001
   -1.6420    0.0027
   -1.5070    0.0010
   -0.4540    0.0104
   -0.2530   -0.0011
   -0.1210   -0.0003
   -0.1040    0.1314
   -0.0140   -0.0010
    0.0160   -0.0002

disp(scores(1:10))

   1.0e+06 *

   -0.0000
   -0.0000
    2.6798
    2.2560
    0.2016
    0.0615
    0.0135
    0.0099
    0.0001
    0.0000

Argumentos de entrada

fun — Función objetivo

identificador de función | nombre de función

Función objetivo, especificada como un identificador de función o un nombre de función. Escriba la función objetivo para aceptar un vector de fila de longitud nvars y devolver un valor escalar.

Cuando la opción 'UseVectorized' es true, escriba fun para aceptar una matriz pop por nvars, donde pop es el tamaño de la población actual. En este caso, fun devuelve un vector de la misma longitud que pop que contiene los valores de la función de aptitud. Asegúrese de que fun no asuma ningún tamaño particular para pop, ya que ga puede pasar un solo miembro de una población incluso en un cálculo vectorizado.

Ejemplo: fun = @(x)(x-[4,2]).^2

Tipos de datos: char | function_handle | string

nvars — Número de variables

entero positivo

Número de variables, especificado como un entero positivo. El solucionador pasa vectores de fila de longitud nvars a fun.

Ejemplo: 4

Tipos de datos: double

A — Restricciones de desigualdad lineales

matriz real

Restricciones de desigualdad lineales, especificadas como una matriz real. A es una matriz M por nvars, donde M es el número de desigualdades.

A codifica las M desigualdades lineales

A*x <= b,

donde x es el vector columna de nvars variables x(:) y b es un vector columna con M elementos.

Por ejemplo, para especificar

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

Dar estas restricciones:

A = [1,2;3,4;5,6];
b = [10;20;30];

Ejemplo: Para especificar que las variables de control suman 1 o menos, proporcione las restricciones A = ones(1,N) y b = 1.

Tipos de datos: double

b — Restricciones de desigualdad lineales

vector real

Restricciones de desigualdad lineales, especificadas como un vector real. b es un vector de M elementos relacionado con la matriz A. Si pasa b como un vector fila, los solvers convierten internamente b en el vector columna b(:).

b codifica las M desigualdades lineales

A*x <= b,

donde x es el vector columna de N variables x(:) y A es una matriz de tamaño M por N.

Por ejemplo, para especificar

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

Dar estas restricciones:

A = [1,2;3,4;5,6];
b = [10;20;30];

Ejemplo: Para especificar que las variables de control suman 1 o menos, proporcione las restricciones A = ones(1,N) y b = 1.

Tipos de datos: double

Aeq — Restricciones de igualdad lineales

matriz real

Restricciones de igualdad lineales, especificadas como una matriz real. Aeq es una matriz Me por nvars, donde Me es el número de igualdades.

Aeq codifica las Me igualdades lineales

Aeq*x = beq,

donde x es el vector columna de N variables x(:) y beq es un vector columna con Me elementos.

Por ejemplo, para especificar

x₁ + 2 x₂ + 3 x₃ = 10
2 x₁ + 4 x₂ + x₃ = 20,

Dar estas restricciones:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Ejemplo: Para especificar que las variables de control suman 1, proporcione las restricciones Aeq = ones(1,N) y beq = 1.

Tipos de datos: double

beq — Restricciones de igualdad lineales

vector real

Restricciones de igualdad lineales, especificadas como un vector real. beq es un vector de Me elementos relacionado con la matriz Aeq. Si pasa beq como un vector fila, los solvers convierten internamente beq en el vector columna beq(:).

beq codifica las Me igualdades lineales

Aeq*x = beq,

donde x es el vector columna de N variables x(:) y Aeq es una matriz de tamaño Meq por N.

Por ejemplo, para especificar

x₁ + 2 x₂ + 3 x₃ = 10
2 x₁ + 4 x₂ + x₃ = 20,

Dar estas restricciones:

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Ejemplo: Para especificar que las variables de control suman 1, proporcione las restricciones Aeq = ones(1,N) y beq = 1.

Tipos de datos: double

lb — Límites inferiores

[] (predeterminado) | vector o arreglo real

Límites inferiores, especificados como un vector real o un arreglo de dobles. lb representa los límites inferiores elemento por elemento en lb ≤ x ≤ ub.

Internamente, ga convierte un arreglo lb en el vector lb(:).

Ejemplo: lb = [0;-Inf;4] significa x(1) ≥ 0, x(3) ≥ 4.

Tipos de datos: double

ub — Límites superiores

[] (predeterminado) | vector o arreglo real

Límites superiores, especificados como un vector real o un arreglo de dobles. ub representa los límites superiores elemento por elemento en lb ≤ x ≤ ub.

Internamente, ga convierte un arreglo ub en el vector ub(:).

Ejemplo: ub = [Inf;4;10] significa x(2) ≤ 4, x(3) ≤ 10.

Tipos de datos: double

nonlcon — Restricciones no lineales

identificador de función | nombre de función

Límites no lineales, especificados como un identificador de función o un nombre de función. nonlcon es una función que acepta un vector o arreglo x y devuelve dos arreglos, c(x) y ceq(x).

• c(x) es el arreglo de restricciones de desigualdad no lineales de x. ga intenta satisfacer

  c(x) <= 0

  para todas las entradas de c .

• ceq(x) es el arreglo de restricciones de igualdad no lineales de x. ga intenta satisfacer

  ceq(x) = 0

  para todas las entradas de ceq .

Por ejemplo:

x = ga(@myfun,4,A,b,Aeq,beq,lb,ub,@mycon)

donde mycon es una función de MATLAB^® como

function [c,ceq] = mycon(x)
c = ...     % Compute nonlinear inequalities at x.
ceq = ...   % Compute nonlinear equalities at x.

Para obtener más información, consulte Restricciones no lineales.

Para aprender a utilizar restricciones vectorizadas, consulte Vectorized Constraints.

Nota

ga no exige que se satisfagan restricciones no lineales cuando la opción PopulationType está establecida en 'bitString' o 'custom'.

Si intcon no está vacío, la segunda salida de nonlcon (ceq) debe ser una entrada vacía ([]).

Para obtener información sobre cómo ga utiliza nonlcon, consulte Algoritmos de resolución de restricciones no lineales para algoritmos genéticos.

Tipos de datos: char | function_handle | string

options — Opciones de optimización

salida de optimoptions | estructura

Opciones de optimización, especificadas como la salida de optimoptions o una estructura.

optimoptions oculta las opciones enumeradas en cursiva. Consulte Options that optimoptions Hides.

• Los valores en {} denotan el valor predeterminado.

• {}* representa el valor predeterminado cuando hay restricciones lineales y para MutationFcn también cuando hay límites.

• I* indica el valor predeterminado para restricciones de números enteros o indica consideraciones especiales para restricciones de números enteros.

• NM indica que la opción no se aplica a gamultiobj.

Opciones para ga y gamultiobj

Opción	Descripción	Valores
ConstraintTolerance	Determina la viabilidad con respecto a restricciones no lineales. Además, max(sqrt(eps),ConstraintTolerance) determina la viabilidad con respecto a las restricciones lineales. Para una estructura de opciones, utilice TolCon .	Escalar no negativo | {1e-3}
CreationFcn	Función que crea la población inicial. Especifique como nombre de una función de creación incorporada o un identificador de función. Consulte Population Options.	{'gacreationuniform'} | {'gacreationlinearfeasible'}* | 'gacreationnonlinearfeasible' | {'gacreationuniformint'}I* para ga | {'gacreationsobol'}I* para gamultiobj | Función de creación personalizada
CrossoverFcn	Función que utiliza el algoritmo para crear hijos cruzados. Especifique como nombre de una función de cruce incorporada o un identificador de función. Consulte Crossover Options.	{'crossoverscattered'} para ga, {'crossoverintermediate'}* para gamultiobj | {'crossoverlaplace'}I* | 'crossoverheuristic' | 'crossoversinglepoint' | 'crossovertwopoint' | 'crossoverarithmetic' | Función de cruce personalizada
CrossoverFraction	La fracción de la población en la siguiente generación, sin incluir a los niños de la élite, que crea la función de cruce.	Escalar no negativo | {0.8}
Display	Nivel de visualización.	'off' | 'iter' | 'diagnose' | {'final'}
DistanceMeasureFcn	Función que calcula la medida de la distancia de los individuos. Especifique como nombre una función de medición de distancia incorporada o un identificador de función. El valor se aplica a la variable de decisión o espacio de diseño (genotipo) o al espacio de función (fenotipo). El valor predeterminado 'distancecrowding' está en el espacio de funciones (fenotipo). Sólo para gamultiobj. Consulte Multiobjective Options. Para una estructura de opciones, utilice un identificador de función, no un nombre.	{'distancecrowding'} significa lo mismo que {@distancecrowding,'phenotype'} | {@distancecrowding,'genotype'} | Función de distancia personalizada
EliteCount	NM Entero positivo que especifica cuántos individuos de la generación actual tienen garantizada la supervivencia hasta la siguiente generación. No se utiliza en gamultiobj .	Número entero no negativo | {ceil(0.05*PopulationSize)} | {0.05*(default PopulationSize)} para problemas de números enteros mixtos
FitnessLimit	NM Si la función de aptitud alcanza el valor de FitnessLimit, el algoritmo se detiene.	Escalar | {-Inf}
FitnessScalingFcn	Función que escala los valores de la función de aptitud. Especifique como nombre de una función de escala incorporada o un identificador de función. Opción no disponible para gamultiobj.	{'fitscalingrank'} | 'fitscalingshiftlinear' | 'fitscalingprop' | 'fitscalingtop' | Función de escala de aptitud personalizada
FunctionTolerance	El algoritmo se detiene si el cambio relativo promedio en el valor de la función de mejor aptitud a lo largo de MaxStallGenerations generaciones es menor o igual a FunctionTolerance. Si StallTest es 'geometricWeighted', entonces el algoritmo se detiene si el cambio relativo promedio ponderado es menor o igual a FunctionTolerance. Para gamultiobj, el algoritmo se detiene cuando el promedio geométrico del cambio relativo en el valor de la dispersión a lo largo de options.MaxStallGenerations generaciones es menor que options.FunctionTolerance, y el spread final es menor que el spread medio a lo largo de las últimas options.MaxStallGenerations generaciones. Consulte gamultiobj Algorithm. Para una estructura de opciones, utilice TolFun .	Escalar no negativo | {1e-6} para ga, {1e-4} para gamultiobj
HybridFcn	I* Función que continúa la optimización después de que ga termina. Especifique como un nombre o un identificador de función. Alternativamente, un arreglo de celdas que especifica la función híbrida y sus opciones. Consulte ga Hybrid Function. Para gamultiobj, la única función híbrida es @fgoalattain. Consulte gamultiobj Hybrid Function. Cuando el problema tiene restricciones de números enteros, no se puede utilizar una función híbrida. Consulte Cuándo utilizar una función híbrida.	Nombre o identificador de la función | 'fminsearch' | 'patternsearch' | 'fminunc' | 'fmincon' | {[]} o Arreglo de celdas de 1 por 2 | {@solver, hybridoptions}, donde solver = fminsearch, patternsearch, fminunc o fmincon {[]}.
InitialPenalty	NM I* Valor inicial del parámetro de penalización	Escalar positivo | {10}
InitialPopulationMatrix	Población inicial utilizada para sembrar el algoritmo genético. Tiene hasta PopulationSize filas y N columnas, donde N es el número de variables. Puede pasar una población parcial, es decir, una con menos de PopulationSize filas. En ese caso, el algoritmo genético utiliza CreationFcn para generar los miembros restantes de la población. Consulte Population Options. Para una estructura de opciones, utilice InitialPopulation .	Matriz | {[]}
InitialPopulationRange	Matriz o vector que especifica el rango de los individuos de la población inicial. Se aplica a la función de creación gacreationuniform. ga desplaza y escala el rango inicial predeterminado para que coincida con cualquier límite finito. Para una estructura de opciones, utilice PopInitRange .	Matriz o vector | {[-10;10]} para componentes no acotados, {[-1e4+1;1e4+1]} para componentes no acotados de problemas con restricciones enteras, {[lb;ub]} para componentes acotados, con el rango predeterminado modificado para que coincida con los límites unilaterales
InitialScoresMatrix	Puntuaciones iniciales utilizadas para determinar la aptitud física. Tiene hasta PopulationSize filas y Nf columnas, donde Nf es el número de funciones de aptitud (1 para ga, mayor que 1 para gamultiobj). Puedes pasar una matriz de puntuaciones parciales, es decir, una con menos de PopulationSize filas. En ese caso, el solucionador completa las puntuaciones cuando evalúa las funciones de aptitud. Para una estructura de opciones, utilice InitialScores .	Vector columna para objetivo único | matriz para multiobjetivo | {[]}
MaxGenerations	Número máximo de iteraciones antes de que el algoritmo se detenga. Para una estructura de opciones, utilice Generations .	Entero no negativo |{100*numberOfVariables} para ga, {200*numberOfVariables} para gamultiobj
MaxStallGenerations	El algoritmo se detiene si el cambio relativo promedio en el valor de la función de mejor aptitud a lo largo de MaxStallGenerations generaciones es menor o igual a FunctionTolerance. Si StallTest es 'geometricWeighted', entonces el algoritmo se detiene si el cambio relativo promedio ponderado es menor o igual a FunctionTolerance. Para gamultiobj, el algoritmo se detiene cuando el promedio geométrico del cambio relativo en el valor de la dispersión a lo largo de options.MaxStallGenerations generaciones es menor que options.FunctionTolerance, y el spread final es menor que el spread medio a lo largo de las últimas options.MaxStallGenerations generaciones. Consulte gamultiobj Algorithm. Para una estructura de opciones, utilice StallGenLimit .	Entero no negativo | {50} para ga, {100} para gamultiobj
MaxStallTime	NM El algoritmo se detiene si no hay mejora en la función objetivo durante MaxStallTime segundos, medidos por tic y toc. Para una estructura de opciones, utilice StallTimeLimit .	Escalar positivo | {Inf}
MaxTime	El algoritmo se detiene después de ejecutarse durante MaxTime segundos, según lo medido por tic y toc. Este límite se aplica después de cada iteración, por lo que ga puede superar el límite cuando una iteración lleva un tiempo considerable. Para una estructura de opciones, utilice TimeLimit .	Escalar no negativo | {Inf}
MigrationDirection	Dirección de la migración. Consulte Migration Options.	'both' | {'forward'}
MigrationFraction	Escalar de 0 a 1 que especifica la fracción de individuos de cada subpoblación que migra a una subpoblación diferente. Consulte Migration Options.	Escalar | {0.2}
MigrationInterval	Entero positivo que especifica el número de generaciones que tienen lugar entre las migraciones de individuos entre subpoblaciones. Consulte Migration Options.	Entero positivo | {20}
MutationFcn	Función que produce hijos de mutación. Especifique como nombre de una función de mutación incorporada o un identificador de función. Consulte Mutation Options.	{'mutationgaussian'} para ga sin restricciones | {'mutationadaptfeasible'}* para gamultiobj y para ga con restricciones | {'mutationpower'}I* | 'mutationpositivebasis' | 'mutationuniform' | Función de mutación personalizada
NonlinearConstraintAlgorithm	Algoritmo de restricción no lineal. Consulte Algoritmos de resolución de restricciones no lineales para algoritmos genéticos. Opción inmutable para gamultiobj . Para una estructura de opciones, utilice NonlinConAlgorithm .	{'auglag'} para ga, {'penalty'} para gamultiobj
OutputFcn	Funciones que ga llama en cada iteración. Especifique como un identificador de función o un arreglo de celdas de identificadores de función. Consulte Output Function Options. Para una estructura de opciones, utilice OutputFcns .	Identificador de función o arreglo de celdas de identificadores de función | {[]}
ParetoFraction	Escalar de 0 a 1 que especifica la fracción de individuos que se deben mantener en el primer frente de Pareto mientras el solucionador selecciona individuos de frentes superiores, solo para gamultiobj. Consulte Multiobjective Options.	Escalar | {0.35}
PenaltyFactor	NM I* Parámetro de actualización de penalización.	Escalar positivo | {100}
PlotFcn	Función que grafica los datos calculados por el algoritmo. Especifique como nombre de una función de gráfico incorporada, un identificador de función o un arreglo de celdas de nombres incorporados o identificadores de función. Consulte Plot Options. Para una estructura de opciones, utilice PlotFcns .	ga o gamultiobj: {[]} | 'gaplotdistance' | 'gaplotgenealogy' | 'gaplotselection' | 'gaplotscorediversity' |'gaplotscores' | 'gaplotstopping' | 'gaplotmaxconstr' | Función de gráfico personalizada ga solamente: 'gaplotbestf' | 'gaplotbestindiv' | 'gaplotexpectation' | 'gaplotrange' gamultiobj solamente: 'gaplotpareto' | 'gaplotparetodistance' | 'gaplotrankhist' | 'gaplotspread'
PlotInterval	Entero positivo que especifica el número de generaciones entre llamadas consecutivas a las funciones de gráfico.	Entero positivo | {1}
PopulationSize	Tamaño de la población.	Entero positivo | {50} cuando numberOfVariables <= 5, {200} en caso contrario | {min(max(10*nvars,40),100)} para problemas con números enteros mixtos
PopulationType	Tipo de datos de la población. Debe ser 'doubleVector' para problemas de números enteros mixtos.	'bitstring' | 'custom' | {'doubleVector'} ga ignora todas las restricciones cuando PopulationType se establece en 'bitString' o 'custom'. Consulte Population Options.
SelectionFcn	Función que selecciona a los padres de los hijos del cruce y de la mutación. Especifique como nombre de una función de selección incorporada o de un identificador de función. gamultiobj utiliza sólo 'selectiontournament'.	{'selectionstochunif'} para ga, {'selectiontournament'} para gamultiobj | 'selectionremainder' | 'selectionuniform' | 'selectionroulette' | Función de selección personalizada
StallTest	NM Tipo de prueba de detención.	'geometricWeighted' | {'averageChange'}
UseParallel	Calcular funciones de aptitud y restricción no lineal en paralelo. Consulte Vectorize and Parallel Options (User Function Evaluation) y Cómo utilizar el procesamiento paralelo en Global Optimization Toolbox.	true | {false}
UseVectorized	Especifica si las funciones están vectorizadas. Consulte Vectorize and Parallel Options (User Function Evaluation) y Vectorize the Fitness Function. Para una estructura de opciones, utilice Vectorized con los valores 'on' o 'off'.	true | {false}

Ejemplo: optimoptions('ga','PlotFcn',@gaplotbestf)

intcon — Variables enteras

vector de números enteros positivos

Variables enteras, especificadas como un vector de números enteros positivos que toman valores de 1 a nvars. Cada valor en intcon representa un componente x que tiene un valor entero.

Nota

Cuando intcon no está vacío, nonlcon debe devolver vacío para ceq. Para obtener más información sobre programación de números enteros, consulte Mixed Integer ga Optimization.

Ejemplo: Para especificar que las entradas pares en x tienen valores enteros, establezca intcon en 2:2:nvars

Tipos de datos: double

problem — Descripción del problema

estructura

Descripción del problema, especificada como una estructura que contiene estos campos.

fitnessfcn	Funciones de aptitud
nvars	Número de variables de diseño
Aineq	Matriz A para restricciones de desigualdad lineales
Bineq	Vector b para restricciones de desigualdad lineales
Aeq	Matriz Aeq para restricciones de igualdad lineales
Beq	Vector beq para restricciones de igualdad lineales
lb	Límite inferior en x
ub	Límite superior en x
nonlcon	Funciones de restricción no lineales
intcon	Índices de variables enteras
rngstate	Campo para reiniciar el estado del generador de números aleatorios
solver	'ga'
options	Opciones creadas usando optimoptions o una estructura de opciones

Debe especificar los campos fitnessfcn, nvars y options. El resto es opcional para ga.

Tipos de datos: struct

Argumentos de salida

x — Solución

vector real

Solución, devuelta como un vector real. x es el mejor punto que ga encontró durante sus iteraciones.

fval — Valor de la función objetivo en la solución

número real

Valor de la función objetivo en la solución, devuelto como un número real. Por lo general, fval = fun(x).

exitflag — Razón por la que ga se ha detenido

valor entero

Razón por la que ga se detuvo y se devolvió como un entero.

Indicador de salida	Significado
1	Sin restricciones no lineales: el cambio acumulativo promedio en el valor de la función de aptitud a lo largo de MaxStallGenerations generaciones es inferior a FunctionTolerance y la vulneración de restricciones es inferior a ConstraintTolerance.
	Con restricciones no lineales: la magnitud de la medida de complementariedad (consulte Medida de complementariedad) es inferior a sqrt(ConstraintTolerance), el subproblema se resuelve utilizando una tolerancia inferior a FunctionTolerance y la vulneración de restricciones es inferior a ConstraintTolerance.
3	El valor de la función de aptitud no ha cambiado en MaxStallGenerations generaciones y la vulneración de restricciones es inferior a ConstraintTolerance.
4	La magnitud del paso es menor que la precisión de la máquina y la infracción de la restricción es menor que ConstraintTolerance.
5	Se ha alcanzado el límite de aptitud mínimo FitnessLimit y la vulneración de restricciones es inferior a ConstraintTolerance.
0	Se ha sobrepasado el número máximo de generaciones MaxGenerations.
-1	Optimización terminada por una función de salida o una función de gráfica.
-2	No se ha encontrado ningún punto factible.
-4	Se ha sobrepasado el límite de tiempo de detención MaxStallTime.
-5	Se ha sobrepasado el límite de tiempo MaxTime.

Cuando existen restricciones de números enteros, ga utiliza el valor de aptitud de penalización en lugar del valor de aptitud para los criterios de detención.

output — Información sobre el proceso de optimización

estructura

Información sobre el proceso de optimización, devuelta como estructura con estos campos:

• problemtype — Tipo de problema, uno de los siguientes:

  • 'unconstrained'

  • 'boundconstraints'

  • 'linearconstraints'

  • 'nonlinearconstr'

  • 'integerconstraints'

• rngstate — Estado del generador de números aleatorios MATLAB, justo antes de que comenzara el algoritmo. Puede utilizar los valores en rngstate para reproducir la salida de ga. Consulte Reproduce Results.

• generations — Número de generaciones calculadas.

• funccount — Número de evaluaciones de la función de aptitud.

• message — Motivo por el cual finalizó el algoritmo.

• maxconstraint — Infracción de restricción máxima, si la hay.

• hybridflag — Indicador de salida de la función híbrida. Se relaciona con HybridFcn options . No aplicable a gamultiobj .

population — Población final

matriz

Población final, devuelta como una matriz PopulationSize por nvars. Las filas de population son los individuos.

scores — Puntuaciones finales

vector columna

Puntuaciones finales, devueltas como un vector de columna.

• Para problemas no enteros, los puntajes finales son los valores de la función de aptitud de las filas de population.

• Para los problemas de números enteros, los puntajes finales son los valores de aptitud de penalización de los miembros de la población. Consulte Integer ga Algorithm.

Más acerca de

Medida de complementariedad

En el solucionador de restricciones no lineales de Lagrange Aumentado, la medida de complementariedad es la norma del vector cuyos elementos son c_iλ_i, donde c_i es la infracción de la restricción de desigualdad no lineal y λ_i es el multiplicador de Lagrange correspondiente. Consulte Algoritmo genético lagrangiano aumentado.

Sugerencias

• Para escribir una función con parámetros adicionales a las variables independientes que pueden ser llamadas por ga, consulte Pasar parámetros adicionales.

• Para los problemas que utilizan el tipo de población Double Vector (el predeterminado), ga no acepta funciones cuyas entradas sean del tipo complex. Para resolver problemas que involucran datos complejos, escriba sus funciones de modo que acepten vectores reales, separando las partes reales e imaginarias.

Algoritmos

Para obtener una descripción del algoritmo genético, consulte Cómo funciona el algoritmo genético.

Para obtener una descripción del algoritmo de programación entera mixta, consulte Integer ga Algorithm.

Para obtener una descripción de los algoritmos de restricción no lineal, consulte Algoritmos de resolución de restricciones no lineales para algoritmos genéticos.

Funcionalidad alternativa

App

La tarea Optimize de Live Editor proporciona una interfaz visual para ga.

Referencias

[1] Goldberg, David E., Genetic Algorithms in Search, Optimization & Machine Learning, Addison-Wesley, 1989.

[2] A. R. Conn, N. I. M. Gould, and Ph. L. Toint. “A Globally Convergent Augmented Lagrangian Algorithm for Optimization with General Constraints and Simple Bounds”, SIAM Journal on Numerical Analysis, Volume 28, Number 2, pages 545–572, 1991.

[3] A. R. Conn, N. I. M. Gould, and Ph. L. Toint. “A Globally Convergent Augmented Lagrangian Barrier Algorithm for Optimization with General Inequality Constraints and Simple Bounds”, Mathematics of Computation, Volume 66, Number 217, pages 261–288, 1997.

Capacidades ampliadas

Soporte paralelo automático

Acelere código mediante la ejecución automática de cálculo paralelo mediante Parallel Computing Toolbox™.

Para ejecutar en paralelo, establezca la opción 'UseParallel' en true.

options = optimoptions('solvername','UseParallel',true)

Para obtener más información, consulte Cómo utilizar el procesamiento paralelo en Global Optimization Toolbox.

Historial de versiones

Introducido antes de R2006a

R2019b: ga realiza menos evaluaciones de la función física

Cuando la función de aptitud es determinista, ga no reevalúa la función de aptitud en individuos de élite (los mejores actuales). Puede controlar este comportamiento accediendo al nuevo campo state.EvalElites y modificándolo en una función de salida personalizada o una función de gráfico personalizada. De manera similar, cuando la población inicial tiene miembros duplicados, ga evalúa cada miembro único solo una vez. Puede controlar este comportamiento en una función de salida personalizada o en una función de gráfico personalizada accediendo y modificando el nuevo campo state.HaveDuplicates. Para obtener más detalles, consulte Custom Output Function for Genetic Algorithm o Función de gráfico personalizada.

Para obtener detalles sobre los dos nuevos campos, consulte The State Structure.

Consulte también

gamultiobj | optimoptions | particleswarm | patternsearch | Optimize

Temas

• Algoritmo genético
• Comience a utilizar Global Optimization Toolbox
• Configuración de problema de optimización basada en solvers