imufilter
Orientación a partir de lecturas de acelerómetro y giroscopio.
Descripción
imufilter System object™ fusiona datos del sensor acelerómetro y giroscopio para estimar la orientación del dispositivo.
Para estimar la orientación del dispositivo:
Cree el objeto
imufiltery configure sus propiedades.Llame al objeto con argumentos, como si fuera una función.
Para más información sobre el funcionamiento de los System objects, consulte ¿Qué son los System Objects?
Creación
Descripción
FUSE = imufilterFUSE, para la fusión de datos del acelerómetro y el giroscopio para estimar la orientación del dispositivo. El filtro utiliza un vector de estado de nueve elementos para rastrear el error en la estimación de la orientación, la estimación del sesgo del giroscopio y la estimación de la aceleración lineal.
FUSE = imufilter('ReferenceFrame',RF)imufilter System object que fusiona datos del acelerómetro y del giroscopio para estimar la orientación del dispositivo en relación con el marco de referencia RF.
FUSE = imufilter(___,Name=Value)
Ejemplo: FUSE = imufilter('SampleRate',200,'GyroscopeNoise',1e-6) crea un System object, FUSE, con una frecuencia de muestreo de 200 Hz y un ruido de giroscopio establecido en 1e-6 radianes por segundo al cuadrado.
Argumentos de entrada
Marco de referencia del filtro, especificado como 'NED' (Noreste-Abajo) o 'ENU' (Este-Norte-Arriba).
Tipos de datos: char | string
Propiedades
A menos que se indique lo contrario, las propiedades son no ajustables, lo que significa que no puede modificar sus valores después de llamar al objeto. Los objetos se bloquean cuando llama a ellos, y la función release los desbloquea.
Si una propiedad es ajustable, puede modificar su valor en cualquier momento.
Para obtener más información sobre cómo modificar los valores de las propiedades, consulte Diseñar sistemas en MATLAB utilizando System objects.
Frecuencia de muestreo de los datos del sensor de entrada en Hz, especificada como un escalar finito positivo.
Ajustable: No
Tipos de datos: single | double | uint8 | uint16 | uint32 | uint64 | int8 | int16 | int32 | int64
Factor de diezmado mediante el cual se reduce la frecuencia de muestreo de los datos del sensor de entrada, especificado como un escalar entero positivo.
El número de filas de las entradas, accelReadings y gyroReadings, debe ser un múltiplo del factor de diezmado.
Ajustable: No
Tipos de datos: single | double | uint8 | uint16 | uint32 | uint64 | int8 | int16 | int32 | int64
Varianza del ruido de la señal del acelerómetro en (m/s2)2, especificada como un escalar real positivo.
Ajustable: Yes
Tipos de datos: single | double | uint8 | uint16 | uint32 | uint64 | int8 | int16 | int32 | int64
Varianza del ruido de la señal del giroscopio en (rad/s)2, especificada como un escalar real positivo.
Ajustable: Yes
Tipos de datos: single | double | uint8 | uint16 | uint32 | uint64 | int8 | int16 | int32 | int64
Varianza de la deriva del giroscopio en (rad/s)2, especificada como un escalar real positivo.
Ajustable: Yes
Tipos de datos: single | double | uint8 | uint16 | uint32 | uint64 | int8 | int16 | int32 | int64
Varianza del ruido de aceleración lineal en (m/s2)2, especificada como un escalar real positivo. La aceleración lineal se modela como un proceso de ruido blanco filtrado de paso bajo.
Ajustable: Yes
Tipos de datos: single | double | uint8 | uint16 | uint32 | uint64 | int8 | int16 | int32 | int64
Factor de caída para la deriva de aceleración lineal, especificado como un escalar en el rango [0,1). Si la aceleración lineal cambia rápidamente, configure LinearAccelerationDecayFactor en un valor más bajo. Si la aceleración lineal cambia lentamente, configure LinearAccelerationDecayFactor en un valor más alto. La deriva de la aceleración lineal se modela como un proceso de ruido blanco filtrado por paso bajo.
Ajustable: Yes
Tipos de datos: single | double | uint8 | uint16 | uint32 | uint64 | int8 | int16 | int32 | int64
Matriz de covarianza para el ruido del proceso, especificada como una matriz de 9 por 9. El valor predeterminado es:
Columns 1 through 6
0.000006092348396 0 0 0 0 0
0 0.000006092348396 0 0 0 0
0 0 0.000006092348396 0 0 0
0 0 0 0.000076154354947 0 0
0 0 0 0 0.000076154354947 0
0 0 0 0 0 0.000076154354947
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
Columns 7 through 9
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0.009623610000000 0 0
0 0.009623610000000 0
0 0 0.009623610000000La matriz de covarianza del proceso inicial tiene en cuenta el error en el modelo de proceso.
Tipos de datos: single | double | uint8 | uint16 | uint32 | uint64 | int8 | int16 | int32 | int64
Formato de orientación de salida, especificado como 'quaternion' o 'Rotation matrix'. El tamaño de la salida depende del tamaño de entrada, N, y del formato de orientación de salida:
'quaternion'–– La salida es un N por 1quaternion.'Rotation matrix'–– La salida es una matriz de rotación de 3 por 3 por N.
Tipos de datos: char | string
Uso
Descripción
[ fusiona las lecturas del acelerómetro y del giroscopio para calcular las mediciones de orientación y velocidad angular. El algoritmo supone que el dispositivo está parado antes de la primera llamada.orientation,angularVelocity,residualData] = FUSE(accelReadings,gyroReadings)
Argumentos de entrada
Lecturas del acelerómetro en el sistema de coordenadas del cuerpo del sensor en m/s2, especificadas como una matriz N por 3. N es el número de muestras y las tres columnas de accelReadings representan las [x y z] mediciones. Se supone que las lecturas del acelerómetro corresponden a la frecuencia de muestreo especificada por la propiedad SampleRate.
Tipos de datos: single | double
Lecturas del giroscopio en el sistema de coordenadas del cuerpo del sensor en rad/s, especificadas como una matriz de N por 3. N es el número de muestras y las tres columnas de gyroReadings representan las [x y z] mediciones. Se supone que las lecturas del giroscopio corresponden a la frecuencia de muestreo especificada por la propiedad SampleRate.
Tipos de datos: single | double
Argumentos de salida
Orientación que puede rotar cantidades de un sistema de coordenadas global a un sistema de coordenadas corporales, devuelta como cuaterniones o un arreglo. El tamaño y el tipo de orientation dependen de si la propiedad OrientationFormat está establecida en 'quaternion' o 'Rotation matrix':
'quaternion'–– La salida es un vector de cuaterniones M por 1, con el mismo tipo de datos subyacente que las entradas.'Rotation matrix'–– La salida es un arreglo de matrices de rotación de 3 por 3 por M del mismo tipo de datos que las entradas.
El número de muestras de entrada, N, y la propiedad DecimationFactor determinan M.
Puede utilizar orientation en una función rotateframe para rotar cantidades desde un sistema de coordenadas global a un sistema de coordenadas del cuerpo del sensor.
Tipos de datos: quaternion | single | double
Velocidad angular con el sesgo del giroscopio eliminado en el sistema de coordenadas del cuerpo del sensor en rad/s, devuelta como un arreglo M por 3. El número de muestras de entrada, N, y la propiedad DecimationFactor determinan M.
Tipos de datos: single | double
Desde R2024a
Datos residuales y de covarianza residual, devueltos como una estructura.
Tipos de datos: struct
Funciones del objeto
Para usar una función de objeto, especifique el System object como el primer argumento de entrada. Por ejemplo, para liberar recursos de sistema de un System object llamado obj, utilice la siguiente sintaxis:
release(obj)
Ejemplos
Cargue el archivo rpy_9axis, que contiene datos registrados de los sensores acelerómetro, giroscopio y magnetómetro de un dispositivo que oscila en cabeceo (alrededor del eje y), luego en guiñada (alrededor del eje z) y luego en balanceo (alrededor del eje x). El archivo también contiene la frecuencia de muestreo de la grabación.
load 'rpy_9axis.mat' sensorData Fs accelerometerReadings = sensorData.Acceleration; gyroscopeReadings = sensorData.AngularVelocity;
Cree un imufilter System object™ con una frecuencia de muestreo establecida en la frecuencia de muestreo de los datos del sensor. Especifique un factor de diezmado de dos para reducir el coste computacional del algoritmo.
decim = 2; fuse = imufilter('SampleRate',Fs,'DecimationFactor',decim);
Pase las lecturas del acelerómetro y del giroscopio al objeto imufilter, fuse, para generar una estimación de la orientación del cuerpo del sensor a lo largo del tiempo. De forma predeterminada, la orientación se genera como un vector de cuaterniones.
q = fuse(accelerometerReadings,gyroscopeReadings);
La orientación se define por el desplazamiento angular requerido para rotar un sistema de coordenadas principal a un sistema de coordenadas secundario. Trazar la orientación en ángulos de Euler en grados a lo largo del tiempo.
La fusión imufilter estima correctamente el cambio de orientación a partir de una orientación inicial asumida orientada al norte. Sin embargo, el eje x del dispositivo apuntaba hacia el sur cuando se grabó. Para estimar correctamente la orientación relativa a la orientación inicial verdadera o relativa a NED, utilice ahrsfilter.
time = (0:decim:size(accelerometerReadings,1)-1)/Fs; plot(time,eulerd(q,'ZYX','frame')) title('Orientation Estimate') legend('Z-axis', 'Y-axis', 'X-axis') xlabel('Time (s)') ylabel('Rotation (degrees)')

Modele una IMU inclinable que contenga un acelerómetro y un giroscopio utilizando imuSensor System object ™. Utilice modelos ideales y realistas para comparar los resultados del seguimiento de orientación utilizando imufilter System object.
Cargue una estructura que describa el movimiento ground-truth y una frecuencia de muestreo. La estructura de movimiento describe rotaciones secuenciales:
guiñada: 120 grados en dos segundos
paso: 60 grados en un segundo
rollo: 30 grados durante medio segundo
balanceo: -30 grados durante medio segundo
tono: -60 grados en un segundo
guiñada: -120 grados durante dos segundos
En la última etapa, la estructura de movimiento combina la primera, segunda y tercera rotación en una rotación de un solo eje. La aceleración, la velocidad angular y la orientación se definen en el sistema de coordenadas NED local.
load y120p60r30.mat motion fs accNED = motion.Acceleration; angVelNED = motion.AngularVelocity; orientationNED = motion.Orientation; numSamples = size(motion.Orientation,1); t = (0:(numSamples-1)).'/fs;
Cree un objeto de sensor IMU ideal y un objeto de filtro IMU predeterminado.
IMU = imuSensor('accel-gyro','SampleRate',fs); aFilter = imufilter('SampleRate',fs);
En un bucle:
Simule la salida de la IMU alimentando el movimiento ground-truth al objeto del sensor de la IMU.
Filtre la salida de la IMU utilizando el objeto de filtro de IMU predeterminado.
orientation = zeros(numSamples,1,'quaternion'); for i = 1:numSamples [accelBody,gyroBody] = IMU(accNED(i,:),angVelNED(i,:),orientationNED(i,:)); orientation(i) = aFilter(accelBody,gyroBody); end release(aFilter)
Trazar la orientación a lo largo del tiempo.
figure(1) plot(t,eulerd(orientation,'ZYX','frame')) xlabel('Time (s)') ylabel('Rotation (degrees)') title('Orientation Estimation -- Ideal IMU Data, Default IMU Filter') legend('Z-axis','Y-axis','X-axis')

Modifique las propiedades de su imuSensor para modelar sensores del mundo real. Ejecute el ciclo nuevamente y trace la estimación de orientación a lo largo del tiempo.
IMU.Accelerometer = accelparams( ... 'MeasurementRange',19.62, ... 'Resolution',0.00059875, ... 'ConstantBias',0.4905, ... 'AxesMisalignment',2, ... 'NoiseDensity',0.003924, ... 'BiasInstability',0, ... 'TemperatureBias', [0.34335 0.34335 0.5886], ... 'TemperatureScaleFactor',0.02); IMU.Gyroscope = gyroparams( ... 'MeasurementRange',4.3633, ... 'Resolution',0.00013323, ... 'AxesMisalignment',2, ... 'NoiseDensity',8.7266e-05, ... 'TemperatureBias',0.34907, ... 'TemperatureScaleFactor',0.02, ... 'AccelerationBias',0.00017809, ... 'ConstantBias',[0.3491,0.5,0]); orientationDefault = zeros(numSamples,1,'quaternion'); for i = 1:numSamples [accelBody,gyroBody] = IMU(accNED(i,:),angVelNED(i,:),orientationNED(i,:)); orientationDefault(i) = aFilter(accelBody,gyroBody); end release(aFilter) figure(2) plot(t,eulerd(orientationDefault,'ZYX','frame')) xlabel('Time (s)') ylabel('Rotation (degrees)') title('Orientation Estimation -- Realistic IMU Data, Default IMU Filter') legend('Z-axis','Y-axis','X-axis')

La capacidad del imufilter para rastrear los datos ground-truth se reduce significativamente cuando se modela una IMU realista. Para mejorar el rendimiento, modifique las propiedades de su objeto imufilter. Estos valores se determinaron empíricamente. Ejecute el ciclo nuevamente y trace la estimación de orientación a lo largo del tiempo.
aFilter.GyroscopeNoise = 7.6154e-7; aFilter.AccelerometerNoise = 0.0015398; aFilter.GyroscopeDriftNoise = 3.0462e-12; aFilter.LinearAccelerationNoise = 0.00096236; aFilter.InitialProcessNoise = aFilter.InitialProcessNoise*10; orientationNondefault = zeros(numSamples,1,'quaternion'); for i = 1:numSamples [accelBody,gyroBody] = IMU(accNED(i,:),angVelNED(i,:),orientationNED(i,:)); orientationNondefault(i) = aFilter(accelBody,gyroBody); end release(aFilter) figure(3) plot(t,eulerd(orientationNondefault,'ZYX','frame')) xlabel('Time (s)') ylabel('Rotation (degrees)') title('Orientation Estimation -- Realistic IMU Data, Nondefault IMU Filter') legend('Z-axis','Y-axis','X-axis')

Para cuantificar el rendimiento mejorado del imufilter modificado, grafique la distancia del cuaternión entre el movimiento de ground-truth y la orientación devuelta por el imufilter con propiedades predeterminadas y no predeterminadas.
qDistDefault = rad2deg(dist(orientationNED,orientationDefault)); qDistNondefault = rad2deg(dist(orientationNED,orientationNondefault)); figure(4) plot(t,[qDistDefault,qDistNondefault]) title('Quaternion Distance from True Orientation') legend('Realistic IMU Data, Default IMU Filter', ... 'Realistic IMU Data, Nondefault IMU Filter') xlabel('Time (s)') ylabel('Quaternion Distance (degrees)')

Este ejemplo muestra cómo eliminar el sesgo del giroscopio de una IMU usando imufilter.
Utilice kinematicTrajectory para crear una trayectoria con dos partes. La primera parte tiene una velocidad angular constante alrededor de los ejes y y z. La segunda parte tiene una velocidad angular variable en los tres ejes.
duration = 60*8; fs = 20; numSamples = duration * fs; rng('default') % Seed the RNG to reproduce noisy sensor measurements. initialAngVel = [0,0.5,0.25]; finalAngVel = [-0.2,0.6,0.5]; constantAngVel = repmat(initialAngVel,floor(numSamples/2),1); varyingAngVel = [linspace(initialAngVel(1), finalAngVel(1), ceil(numSamples/2)).', ... linspace(initialAngVel(2), finalAngVel(2), ceil(numSamples/2)).', ... linspace(initialAngVel(3), finalAngVel(3), ceil(numSamples/2)).']; angVelBody = [constantAngVel; varyingAngVel]; accBody = zeros(numSamples,3); traj = kinematicTrajectory('SampleRate',fs); [~,qNED,~,accNED,angVelNED] = traj(accBody,angVelBody);
Crea un imuSensor System object ™, IMU, con un giroscopio no ideal. Llame a IMU con la aceleración, la velocidad angular y la orientación de la ground-truth .
IMU = imuSensor('accel-gyro', ... 'Gyroscope',gyroparams('RandomWalk',0.003,'ConstantBias',0.3), ... 'SampleRate',fs); [accelReadings, gyroReadingsBody] = IMU(accNED,angVelNED,qNED);
Crea un imufilter System object, fuse. Llame a fuse con las lecturas del acelerómetro y del giroscopio modelados.
fuse = imufilter('SampleRate',fs, 'GyroscopeDriftNoise', 1e-6); [~,angVelBodyRecovered] = fuse(accelReadings,gyroReadingsBody);
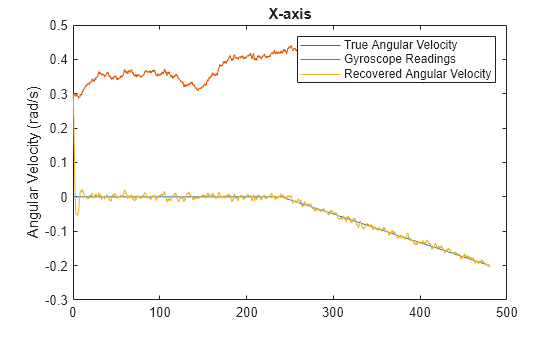
Trace la velocidad angular ground-truth, las lecturas del giroscopio y la velocidad angular recuperada para cada eje.
La velocidad angular devuelta desde imufilter compensa el efecto del sesgo del giroscopio a lo largo del tiempo y converge a la velocidad angular real.
time = (0:numSamples-1)'/fs; figure(1) plot(time,angVelBody(:,1), ... time,gyroReadingsBody(:,1), ... time,angVelBodyRecovered(:,1)) title('X-axis') legend('True Angular Velocity', ... 'Gyroscope Readings', ... 'Recovered Angular Velocity') ylabel('Angular Velocity (rad/s)')
figure(2) plot(time,angVelBody(:,2), ... time,gyroReadingsBody(:,2), ... time,angVelBodyRecovered(:,2)) title('Y-axis') ylabel('Angular Velocity (rad/s)')

figure(3) plot(time,angVelBody(:,3), ... time,gyroReadingsBody(:,3), ... time,angVelBodyRecovered(:,3)) title('Z-axis') ylabel('Angular Velocity (rad/s)') xlabel('Time (s)')

Algoritmos
Nota: El siguiente algoritmo sólo se aplica a un marco de referencia NED.
imufilter utiliza la estructura de filtro Kalman de seis ejes descrita en [1]. El algoritmo intenta rastrear los errores de orientación, desplazamiento del giroscopio y aceleración lineal para generar la orientación final y la velocidad angular. En lugar de rastrear la orientación directamente, el filtro Kalman indirecto modela el proceso de error, x, con una actualización recursiva:
donde xk es un vector de 9 por 1 que consta de:
θk –– Vector de error de orientación de 3 por 1, en radianes, en el tiempo k
bk –– Vector de sesgo de velocidad angular cero del giroscopio 3 por 1, en radianes por segundo, en el tiempo k
ak –– Vector de error de aceleración de 3 por 1 medido en el marco del sensor, en g, en el tiempo k
wk –– Vector de ruido aditivo de 9 por 1
Fk –– modelo de transición de estados
Dado que xk se define como el proceso de error, la estimación a priori siempre es cero y, por lo tanto, el modelo de transición de estado, Fk, es cero. Esta idea da como resultado la siguiente reducción de las ecuaciones estándar de Kalman:
Ecuaciones de Kalman estándar:
Ecuaciones de Kalman utilizadas en este algoritmo:
donde
xk− –– estimación del estado predicho (a priori); el proceso de error
Pk− –– estimación de covarianza prevista (a priori)
yk –– innovación
Sk –– covarianza de la innovación
Kk –– Ganancia de Kalman
xk+ –– estimación de estado actualizada (a posteriori)
Pk+ –– estimación de covarianza actualizada (a posteriori)
k representa la iteración, el superíndice + representa una estimación a posteriori y el superíndice − representa una estimación a priori.
El gráfico y los siguientes pasos describen una iteración basada en un solo cuadro a través del algoritmo.

Antes de la primera iteración, las entradas accelReadings y gyroReadings se dividen en cuadros de 1 por 3 y cuadros de DecimationFactor por 3, respectivamente. El algoritmo utiliza las lecturas del acelerómetro más actuales correspondientes a la mayor parte de las lecturas del giroscopio.
Siga el algoritmo para obtener una explicación de cada etapa de la descripción detallada.

El algoritmo modela la aceleración y el cambio angular como procesos lineales.

La orientación del cuadro actual se predice estimando primero el cambio angular respecto del cuadro anterior:
donde N es el factor de diezmado especificado por la propiedad DecimationFactor, y fs es la frecuencia de muestreo especificada por la propiedad SampleRate. Los paréntesis indican las dimensiones de la matriz.
El cambio angular se convierte en cuaterniones utilizando la sintaxis de construcción rotvec quaternion:
La estimación de orientación anterior se actualiza girándola por Δ Q:
Durante la primera iteración, la estimación de orientación, q−, se inicializa mediante ecompass con el supuesto de que el eje x apunta al norte.
El vector de gravedad se interpreta como la tercera columna del cuaternión, q−, en forma de matriz de rotación:
Consulte ecompass para obtener una explicación de por qué la tercera columna de rPrior puede interpretarse como el vector de gravedad.
Se realiza una segunda estimación del vector de gravedad restando la estimación de aceleración lineal decaida de la iteración anterior de las lecturas del acelerómetro:
El modelo de error es la diferencia entre la estimación de la gravedad de las lecturas del acelerómetro y la estimación de la gravedad de las lecturas del giroscopio: .

Las ecuaciones de Kalman utilizan la estimación de gravedad derivada de las lecturas del giroscopio, g, y la observación del proceso de error, z, para actualizar las matrices de ganancia de Kalman y de covarianza intermedia. La ganancia de Kalman se aplica a la señal de error, z, para generar una estimación de error a posteriori, x+.

El modelo de observación asigna el estado observado de 1 por 3, g, al estado real de 3 por 9, H.
El modelo de observación se construye como:
donde gx, gy y gz son los elementos x, y y z del vector de gravedad estimado a partir de la orientación, respectivamente. κ es una constante determinada por las propiedades SampleRate y DecimationFactor: κ = DecimationFactor/SampleRate.
Consulte las secciones 7.3 y 7.4 de [1] para obtener una derivación del modelo de observación.
La covarianza de innovación es una matriz de 3 por 3 que se utiliza para rastrear la variabilidad en las mediciones. La matriz de covarianza de innovación se calcula como:
donde
H es la matriz del modelo de observación
P− es la estimación predicha (a priori) de la covarianza del modelo de observación calculado en la iteración anterior
R es la covarianza del ruido del modelo de observación, calculada como:
Las siguientes propiedades definen la varianza del ruido del modelo de observación:
κ –– (DecimationFactor/SampleRate)2
β –– GyroscopeDriftNoise
η –– GyroscopeNoise
λ –– AccelerometerNoise
La covarianza de la estimación del error es una matriz de 9 por 9 que se utiliza para rastrear la variabilidad en el estado.
La matriz de covarianza de estimación de error se actualiza como:
donde K es la ganancia de Kalman, H es la matriz de medición y P− es la covarianza de estimación de error calculada durante la iteración anterior.
La covarianza de la estimación del error es una matriz de 9 por 9 que se utiliza para rastrear la variabilidad en el estado. La covarianza de estimación de error a priori, P−, se establece en la covarianza de ruido del proceso, Q, determinada durante la iteración anterior. Q se calcula como una función de la covarianza de estimación de error a posteriori, P+. Al calcular Q, se supone que los términos de correlación cruzada son insignificantes en comparación con los términos de autocorrelación y se establecen en cero:
dónde
P+ –– es la covarianza de estimación de error actualizada (a posteriori)
β –– GyroscopeDriftNoise
η –– GyroscopeNoise
Consulte la sección 10.1 de [1] para obtener una derivación de los términos de la matriz de error del proceso.
La matriz de ganancia de Kalman es una matriz de 9 por 3 que se utiliza para ponderar la innovación. En este algoritmo, la innovación se interpreta como el proceso de error, z.
La matriz de ganancia de Kalman se construye como:
donde
P- –– covarianza del error previsto
H –– modelo de observación
S –– covarianza de la innovación
La estimación del error a posterior se determina combinando la matriz de ganancia de Kalman con el error en las estimaciones del vector de gravedad:

La estimación de orientación se actualiza multiplicando la estimación anterior por el error:
La estimación de la aceleración lineal se actualiza decayendo la estimación de la aceleración lineal de la iteración anterior y restando el error:
donde
La estimación del desplazamiento del giroscopio se actualiza restando el error de desplazamiento del giroscopio del desplazamiento del giroscopio de la iteración anterior:
Para estimar la velocidad angular, se promedia el marco de gyroReadings y se resta el desplazamiento del giroscopio calculado en la iteración anterior:
donde N es el factor de diezmado especificado por la propiedad DecimationFactor.
La estimación de compensación del giroscopio se inicializa en ceros para la primera iteración.
Referencias
[1] Open Source Sensor Fusion. https://github.com/memsindustrygroup/Open-Source-Sensor-Fusion/tree/master/docs
[2] Roetenberg, D., H.J. Luinge, C.T.M. Baten, and P.H. Veltink. "Compensation of Magnetic Disturbances Improves Inertial and Magnetic Sensing of Human Body Segment Orientation." IEEE Transactions on Neural Systems and Rehabilitation Engineering. Vol. 13. Issue 3, 2005, pp. 395-405.
Capacidades ampliadas
Indicaciones y limitaciones de uso:
Consulte System Objects in MATLAB Code Generation (MATLAB Coder).
Este System object también admite la generación estricta de código de precisión simple.
Historial de versiones
Introducido en R2018bObjeto imufilter, FUSE devuelve un tercer argumento de salida, residualData, que contiene residuos y covarianza residual almacenados como una estructura.
Consulte también
ecompass | imuSensor | ahrsfilter | gpsSensor
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)