La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

bsplinepolytraj

Generar trayectorias polinómicas con B-splines

Desde R2019a

Sintaxis

[q,qd,qdd,pp] = bsplinepolytraj(controlPoints,tInterval,tSamples)

Descripción

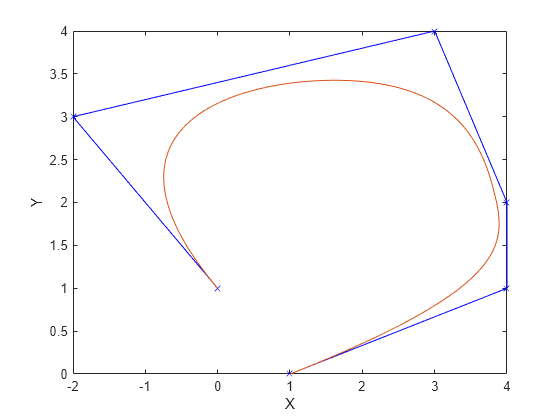
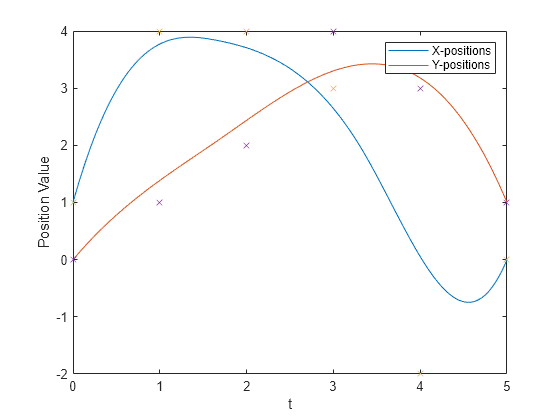
[q,qd,qdd,pp] = bsplinepolytraj(controlPoints,tInterval,tSamples) genera una trayectoria B-spline cúbica por tramos que cae en el polígono de control definido por controlPoints. La trayectoria se muestrea uniformemente entre los tiempos de inicio y fin dados en tInterval. La función devuelve las posiciones, velocidades y aceleraciones de las muestras de tiempo de entrada, tSamples. También devuelve la forma polinómica por tramos pp de la trayectoria polinómica con relación al tiempo.

Ejemplos

Calcular la trayectoria B-spline para movimientos planos en 2D

Utilice la función bsplinepolytraj con un conjunto determinado de puntos de control xy en 2D. La B-spline utiliza estos puntos de control para crear una trayectoria dentro del polígono. También se indican los tiempos de inicio y fin de la trayectoria.

cpts = [1 4 4 3 -2 0; 0 1 2 4 3 1];
tpts = [0 5];

Calcule la trayectoria B-spline. La función genera las posiciones de la trayectoria, (q), la velocidad (qd), la aceleración (qdd), el vector de tiempo (tvec) y los coeficientes polinómicos (pp) del polinomio que alcanza los waypoints utilizando los puntos de control.

tvec = 0:0.01:5;
[q, qd, qdd, pp] = bsplinepolytraj(cpts,tpts,tvec);

Represente los resultados. Muestre los puntos de control y la trayectoria resultante dentro de ellos.

figure
plot(cpts(1,:),cpts(2,:),'xb-')
hold all
plot(q(1,:), q(2,:))
xlabel('X')
ylabel('Y')
hold off

Represente la posición de cada uno de los elementos de la trayectoria B-spline. Estas trayectorias son polinomios cúbicos por tramos parametrizados en el tiempo.

figure
plot(tvec,q)
hold all
plot([0:length(cpts)-1],cpts,'x')
xlabel('t')
ylabel('Position Value')
legend('X-positions','Y-positions')
hold off

Interpolar con B-spline

Cree waypoints para interpolarlos con una B-spline.

wpts1 = [0 1 2.1 8 4 3];
wpts2 = [0 1 1.3 .8 .3 .3];
wpts = [wpts1; wpts2];
L = length(wpts) - 1;

Forme matrices utilizadas para calcular los puntos internos del polígono de control.

r = zeros(L+1, size(wpts,1));
A = eye(L+1);
for i= 1:(L-1)
    A(i+1,(i):(i+2)) = [1 4 1];
    r(i+1,:) = 6*wpts(:,i+1)';
end

Anule los puntos finales, y seleccione r0 y rL.

A(2,1:3) = [3/2 7/2 1]; 
A(L,(L-1):(L+1)) = [1 7/2 3/2]; 

r(1,:) = (wpts(:,1) + (wpts(:,2) - wpts(:,1))/2)';
r(end,:) = (wpts(:,end-1) + (wpts(:,end) - wpts(:,end-1))/2)';

dInterior = (A\r)';

Construya un polígono de control completo y use bsplinepolytraj para calcular un polinomio con nuevos puntos de control.

cpts = [wpts(:,1) dInterior wpts(:,end)];
t = 0:0.01:1;
q = bsplinepolytraj(cpts, [0 1], t);

Represente los resultados. Muestre los waypoints originales, el polígono calculado y la B-spline interpolada.

figure;
hold all
plot(wpts1, wpts2, 'o');
plot(cpts(1,:), cpts(2,:), 'x-');
plot(q(1,:), q(2,:));
legend('Original waypoints', 'Computed control polygon', 'B-spline');

[1] Farin, Sección 9.1

Argumentos de entrada

controlPoints — Puntos del polígono de control

matriz de n por p

Puntos del polígono de control de la trayectoria B-spline, especificados como una matriz de n por p, en la que n es la dimensión de la trayectoria y p es el número de puntos de control.

Ejemplo: [1 4 4 3 -2 0; 0 1 2 4 3 1]

Tipos de datos: single | double

tInterval — Tiempos de inicio y fin de la trayectoria

vector de dos elementos

Tiempos de inicio y finalización de la trayectoria, especificados como un vector de dos elementos.

Ejemplo: [0 10]

Tipos de datos: single | double

tSamples — Muestras de tiempo de la trayectoria

vector

Muestras de tiempo de la trayectoria, especificadas como vector. La posición de salida, q, la velocidad, qd, y las aceleraciones, qdd, se muestrean en estos intervalos de tiempo.

Ejemplo: 0:0.01:10

Tipos de datos: single | double

Argumentos de salida

q — Posiciones de trayectoria

vector

Posiciones de la trayectoria en las muestras de tiempo dadas en tSamples, devueltas como vector.

Tipos de datos: single | double

qd — Velocidades de trayectoria

vector

Velocidades de la trayectoria en las muestras de tiempo dadas en tSamples, devueltas como vector.

Tipos de datos: single | double

qdd — Aceleraciones de trayectoria

vector

Aceleraciones de la trayectoria en las muestras de tiempo dadas en tSamples, devueltas como vector.

Tipos de datos: single | double

pp — Polinomio por tramos

estructura

Polinomio por tramos, devuelto como una estructura que define el polinomio de cada sección de la trayectoria por tramos. Puede crear sus propios polinomios por tramos utilizando mkpp, o evaluar el polinomio en los tiempos especificados mediante ppval. La estructura contiene los siguientes campos:

• form: 'pp'.

• breaks: el vector de p elementos de los tiempos en los que la trayectoria por tramos cambia de forma. p es el número de waypoints.

• coefs: matriz de n (p–1) por order para los coeficientes de los polinomios. n (p–1) es la dimensión de la trayectoria multiplicada por el número de pieces. Cada conjunto de n filas define los coeficientes del polinomio que ha descrito cada trayectoria variable.

• pieces: p–1. El número de breaks menos 1.

• order: El grado del polinomio +1. Por ejemplo, los polinomios cúbicos son de grado cuatro.

• dim: n. La dimensión de las posiciones de los puntos de control.

Referencias

[1] Farin, Gerald E. Curves and Surfaces for Computer Aided Geometric Design: A Practical Guide. San Diego, CA: Academic Press, 1993.

Capacidades ampliadas

Generación de código C/C++
Genere código C y C++ mediante MATLAB® Coder™.

Historial de versiones

Introducido en R2019a

Consulte también

contopptraj | cubicpolytraj | quinticpolytraj | rottraj | transformtraj | trapveltraj

×

Abrir ejemplo

Tiene una versión modificada de este ejemplo. ¿Desea abrir este ejemplo con sus modificaciones?

No, sobrescribir la versión modificada Sí