La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

trapveltraj

Generar trayectorias con perfiles de velocidad trapezoidal

Sintaxis

[q,qd,qdd,tSamples,pp] = trapveltraj(wayPoints,numSamples)

[q,qd,qdd,tSamples,pp] = trapveltraj(wayPoints,numSamples,Name,Value)

Descripción

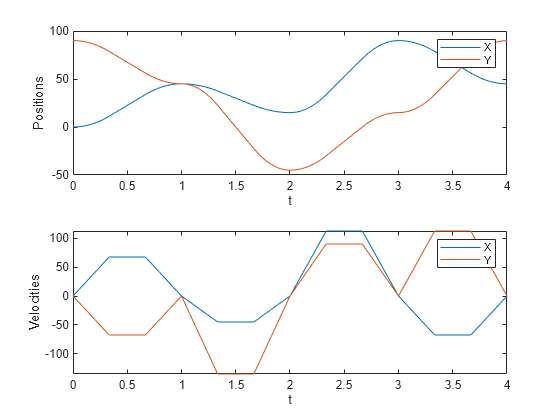
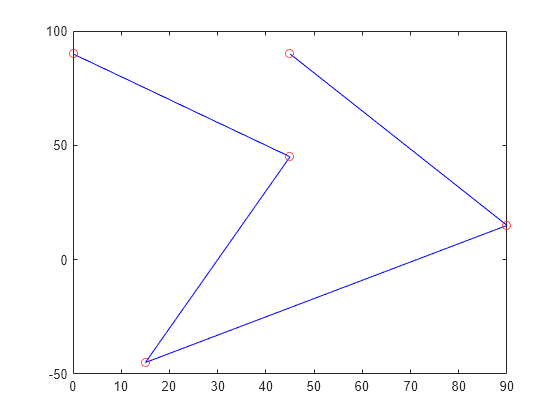
[q,qd,qdd,tSamples,pp] = trapveltraj(wayPoints,numSamples) genera una trayectoria a través de un conjunto dado de waypoints de entrada que siguen un perfil de velocidad trapezoidal. La función genera las posiciones, velocidades y aceleraciones de las muestras de tiempo dadas, tSamples, basándose en el número de muestras especificado, numSamples. También devuelve la forma polinómica por tramos pp de la trayectoria polinómica con relación al tiempo.

[q,qd,qdd,tSamples,pp] = trapveltraj(wayPoints,numSamples,Name,Value) especifica parámetros adicionales usando argumentos de par Name,Value.

Ejemplos

Calcular la trayectoria de velocidad trapezoidal para movimientos planos en 2D

Utilice la función trapveltraj con un conjunto determinado de waypoints xy en 2D.

wpts = [0 45 15 90 45; 90 45 -45 15 90];

Calcule la trayectoria para un número de muestras determinado (501). La función genera las posiciones de la trayectoria, (q), la velocidad (qd), la aceleración (qdd), el vector de tiempo (tvec) y los coeficientes polinómicos (pp) del polinomio que alcanza los waypoints utilizando velocidades trapezoidales.

[q,qd,qdd,tvec,pp] = trapveltraj(wpts,501);

Represente las trayectorias de las posiciones x e y y el perfil de velocidad trapezoidal entre cada waypoint.

subplot(2,1,1)
plot(tvec, q)
xlabel('t')
ylabel('Positions')
legend('X','Y')
subplot(2,1,2)
plot(tvec, qd)
xlabel('t')
ylabel('Velocities')
legend('X','Y')

También puede verificar las posiciones reales en el plano 2D. Represente las diferentes filas del vector q y los waypoints como las posiciones x e y.

figure
plot(q(1,:),q(2,:),'-b',wpts(1,:),wpts(2,:),'or')

Argumentos de entrada

wayPoints — Waypoints para una trayectoria

matriz de n por p

Puntos de los waypoints de la trayectoria, especificados como una matriz de n por p, en la que n es la dimensión de la trayectoria y p es el número de waypoints.

Ejemplo: [1 4 4 3 -2 0; 0 1 2 4 3 1]

Tipos de datos: single | double

numSamples — Número de muestras en la trayectoria de salida

número entero positivo

Número de muestras en la trayectoria de salida, especificado como un número entero positivo.

Tipos de datos: single | double

Argumentos de par nombre-valor

Especifique pares de argumentos opcionales como Name1=Value1,...,NameN=ValueN, donde Name es el nombre del argumento y Value es el valor correspondiente. Los argumentos nombre-valor deben aparecer después de los otros argumentos, pero el orden de los pares no importa.

En versiones anteriores a R2021a, use comas para separar cada nombre y valor, y encierre Name entre comillas.

Ejemplo: 'PeakVelocity',5

Nota

Debido a la naturaleza del perfil de velocidad trapezoidal, solo puede definir como máximo dos de los siguientes parámetros.

PeakVelocity — Velocidad máxima del perfil de velocidad

escalar | Vector de n elementos | matriz de n por (p–1)

Velocidad máxima del segmento de perfil, especificada como un par separado por comas compuesto por 'PeakVelocity' y un escalar, un vector o una matriz. Esta velocidad máxima es la velocidad más alta alcanzada durante el perfil de velocidad trapezoidal.

Se aplica un valor escalar a todos los elementos de la trayectoria y entre todos los waypoints. Se aplica un vector de n elementos a cada elemento de la trayectoria entre todos los waypoints. Se aplica una matriz de n por (p–1) a cada elemento de la trayectoria para cada waypoint.

Tipos de datos: single | double

Acceleration — Aceleración del perfil de velocidad

escalar | Vector de n elementos | matriz de n por (p–1)

Aceleración del perfil de velocidad, especificada como un par separado por comas compuesto por 'Acceleration' y un escalar, un vector o una matriz. Esta aceleración define la aceleración constante desde la velocidad cero hasta el valor PeakVelocity.

Se aplica un valor escalar a todos los elementos de la trayectoria y entre todos los waypoints. Se aplica un vector de n elementos a cada elemento de la trayectoria entre todos los waypoints. Se aplica una matriz de n por (p–1) a cada elemento de la trayectoria para cada waypoint.

Tipos de datos: single | double

EndTime — Duración de cada segmento de trayectoria

escalar | Vector de n elementos | matriz de n por (p–1)

Duración de cada uno de los segmentos de trayectoria p–1, especificada como un par separado por comas compuesto por 'EndTime' y un escalar, un vector o una matriz.

Se aplica un valor escalar a todos los elementos de la trayectoria y entre todos los waypoints. Se aplica un vector de n elementos a cada elemento de la trayectoria entre todos los waypoints. Se aplica una matriz de n por (p–1) a cada elemento de la trayectoria para cada waypoint.

Tipos de datos: single | double

AccelTime — Duración de la fase de aceleración del perfil de velocidad

escalar | Vector de n elementos | matriz de n por (p–1)

Duración de la fase de aceleración del perfil de velocidad, especificada como un par separado por comas compuesto por 'AccelTime' y un escalar, un vector o una matriz.

Se aplica un valor escalar a todos los elementos de la trayectoria y entre todos los waypoints. Se aplica un vector de n elementos a cada elemento de la trayectoria entre todos los waypoints. Se aplica una matriz de n por (p–1) a cada elemento de la trayectoria para cada waypoint.

Tipos de datos: single | double

Argumentos de salida

q — Posiciones de trayectoria

matriz de n por m

Posiciones de la trayectoria en las muestras de tiempo dadas en tSamples, devueltas como una matriz de n por m, donde n es la dimensión de la trayectoria y m es igual a numSamples.

Tipos de datos: single | double

qd — Velocidades de trayectoria

matriz de n por m

Velocidades de la trayectoria en las muestras de tiempo dadas en tSamples, devueltas como una matriz de n por m, donde n es la dimensión de la trayectoria y m es igual a numSamples.

Tipos de datos: single | double

qdd — Aceleraciones de trayectoria

matriz de n por m

Aceleraciones de la trayectoria en las muestras de tiempo dadas en tSamples, devueltas como una matriz de n por m, donde n es la dimensión de la trayectoria y m es igual a numSamples.

Tipos de datos: single | double

tSamples — Muestras de tiempo de la trayectoria

Vector de m elementos

Muestras de tiempo de la trayectoria, devueltas como un vector de m elementos. La posición de salida, q, la velocidad, qd, y las aceleraciones, qdd, se muestrean en estos intervalos de tiempo.

Ejemplo: 0:0.01:10

Tipos de datos: single | double

pp — Polinomios por tramos

arreglo de celdas de estructuras

Polinomio por tramos, devuelto como un arreglo de celdas de estructuras que define el polinomio de cada sección de la trayectoria por tramos. Si todos los elementos de la trayectoria comparten las mismas rupturas, el arreglo de celdas es una única estructura polinomial por tramos. De lo contrario, el arreglo de celdas tiene n elementos, que corresponden a cada uno de los diferentes elementos de la trayectoria (dimensiones). Cada estructura contiene los siguientes campos:

• form: 'pp'.

• breaks: el vector de p elementos de los tiempos en los que la trayectoria por tramos cambia de forma. p es el número de waypoints.

• coefs: matriz de n (p–1) por order para los coeficientes de los polinomios. n (p–1) es la dimensión de la trayectoria multiplicada por el número de pieces. Cada conjunto de n filas define los coeficientes del polinomio que ha descrito cada trayectoria variable.

• pieces: p–1. El número de breaks menos 1.

• order: El grado del polinomio +1. Por ejemplo, los polinomios cúbicos son de grado cuatro.

• dim: n. La dimensión de las posiciones de los puntos de control.

Puede crear sus propios polinomios por tramos utilizando mkpp, o evaluar el polinomio en los tiempos especificados mediante ppval.

pp — Polinomio por tramos

estructura

Polinomio por tramos, devuelto como una estructura que define el polinomio de cada sección de la trayectoria por tramos. Puede crear sus propios polinomios por tramos utilizando mkpp, o evaluar el polinomio en los tiempos especificados mediante ppval. La estructura contiene los siguientes campos:

• form: 'pp'.

• breaks: el vector de p elementos de los tiempos en los que la trayectoria por tramos cambia de forma. p es el número de waypoints.

• coefs: matriz de n (p–1) por order para los coeficientes de los polinomios. n (p–1) es la dimensión de la trayectoria multiplicada por el número de pieces. Cada conjunto de n filas define los coeficientes del polinomio que ha descrito cada trayectoria variable.

• pieces: p–1. El número de breaks menos 1.

• order: El grado del polinomio +1. Por ejemplo, los polinomios cúbicos son de grado cuatro.

• dim: n. La dimensión de las posiciones de los puntos de control.

Referencias

[1] Lynch, Kevin M., and Frank C. Park. Modern Robotics: Mechanics, Planning and Control. Cambridge: Cambridge University Press, 2017.

[2] Spong, Mark W., Seth Hutchinson, and M. Vidyasagar. Robot Modeling and Control. John Wiley & Sons, 2006.

Capacidades ampliadas

Generación de código C/C++
Genere código C y C++ mediante MATLAB® Coder™.

Historial de versiones

Introducido en R2019a

Consulte también

bsplinepolytraj | contopptraj | cubicpolytraj | quinticpolytraj | rottraj | transformtraj

Temas

• Design Trajectory with Velocity Limits Using Trapezoidal Velocity Profile