Main Content

La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

differentialDriveKinematics

Modelo de vehículo con tracción diferencial

expandir todo en la página

Descripción

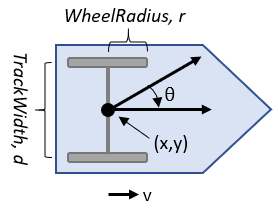
differentialDriveKinematics crea un modelo de vehículo con tracción diferencial para simular dinámicas de vehículos simplificadas. Este modelo se aproxima a un vehículo con un solo eje fijo y ruedas separadas por un ancho de vía especificado. Las ruedas se pueden dirigir de forma independiente. La velocidad y la dirección del vehículo se definen desde el centro del eje. El estado del vehículo se define como un vector de tres elementos, [x y theta], con la posición global xy especificada en metros, y la dirección del vehículo, theta, especificado en radianes. Para calcular los estados de las derivadas de tiempo del modelo, use la función derivative con comandos de entrada y el estado actual del robot.

Creación

Sintaxis

kinematicModel = differentialDriveKinematics
kinematicModel = differentialDriveKinematics(Name,Value)

Descripción

kinematicModel = differentialDriveKinematics crea un objeto de modelo cinemático con tracción diferencial y valores de propiedad predeterminados.

ejemplo

kinematicModel = differentialDriveKinematics(Name,Value) establece las propiedades del objeto en el valor especificado. Puede especificar varias propiedades en el orden que desee.

Propiedades

expandir todo

Radio de las ruedas del vehículo, especificado en metros.

El rango de velocidad del vehículo es un vector de dos elementos que proporciona la velocidad mínima y máxima del vehículo, [MinSpeed MaxSpeed], especificada en metros por segundo.

El ancho de vía del vehículo hace referencia a la distancia entre las ruedas, o la longitud del eje, especificada en metros.

La propiedad VehicleInputs especifica el formato de los comandos de entrada del modelo cuando se usa la función derivative. Las opciones se especifican como una de las siguientes cadenas:

  • "WheelSpeeds": las velocidades angulares de cada una de las ruedas, especificadas en radianes por segundo.

  • "VehicleSpeedHeadingRate": la velocidad del vehículo y la velocidad angular de la dirección, especificadas en metros y en radianes por segundo, respectivamente.

Funciones del objeto

derivativeDerivada de tiempo del estado del vehículo

Ejemplos

contraer todo

Abrir script en vivo

Crear un robot

Defina un robot y establezca la posición de partida inicial y la orientación.

kinematicModel = differentialDriveKinematics;
initialState = [0 0 0];

Simular el movimiento del robot

Establezca la escala de tiempo de la simulación en 1 s con unidades de tiempo de 0.05 s, los comandos de entrada en 50 rad/s para la rueda izquierda y 40 rad/s para la rueda derecha para crear un giro a la derecha. Simule el movimiento del robot utilizando el solver ode45 en la función derivative.

tspan = 0:0.05:1;
inputs = [50 40]; %Left wheel is spinning faster
[t,y] = ode45(@(t,y)derivative(kinematicModel,y,inputs),tspan,initialState);

Representar la ruta

figure
plot(y(:,1),y(:,2))

Referencias

[1] Lynch, Kevin M., and Frank C. Park. Modern Robotics: Mechanics, Planning, and Control 1st ed. Cambridge, MA: Cambridge University Press, 2017.

Capacidades ampliadas

Generación de código C/C++
Genere código C y C++ mediante MATLAB® Coder™.

Historial de versiones

Introducido en R2019b

Consulte también

Clases

Bloques

Funciones

Temas