tf2ss

Convertir los parámetros del filtro de la función de transferencia a la forma del espacio de estados

Sintaxis

[A,B,C,D] = tf2ss(b,a)

Descripción

[A,B,C,D] = tf2ss(b,a) convierte una función de transferencia de una entrada en tiempo continuo o en tiempo discreto en una representación equivalente del espacio de estados.

Ejemplos

Convertir la función de transferencia en forma de espacio de estados

Considere el sistema descrito por la función de transferencia

$$H(s)=\frac{\left[\begin{array}{c}2s+3\\ s^2+2s+1\end{array}\right]}{s^2+0.4s+1}.$$

Conviértalo en forma de espacio de estados utilizando tf2ss.

b = [0 2 3; 1 2 1];
a = [1 0.4 1];
[A,B,C,D] = tf2ss(b,a)

A = 2×2

   -0.4000   -1.0000
    1.0000         0

B = 2×1

     1
     0

C = 2×2

    2.0000    3.0000
    1.6000         0

D = 2×1

     0
     1

Sistema masa-muelle

Un sistema oscilante unidimensional de tiempo discreto consiste en una masa unitaria, $\mathit{m}$, unida a una pared por un muelle de constante elástica unitaria. Un sensor muestrea la aceleración, $\mathit{a}$, de la masa a ${\mathit{F}}_{\mathrm{s}}=5$ Hz.

Genere 50 muestras de tiempo. Defina el intervalo de muestreo $\Delta \mathit{t}=1/{\mathit{F}}_{\mathrm{s}}$.

Fs = 5;
dt = 1/Fs;
N = 50;
t = dt*(0:N-1);
u = [1 zeros(1,N-1)];

La función de transferencia del sistema tiene una expresión analítica:

$\mathit{H}\left(\mathit{z}\right)=\frac{1-{\mathit{z}}^{-1}\left(1+\cos \Delta \mathit{t}\right)+{\mathit{z}}^{-2}\cos \Delta \mathit{t}}{1-2{\mathit{z}}^{-1}\cos \Delta \mathit{t}+{\mathit{z}}^{-2}}$.

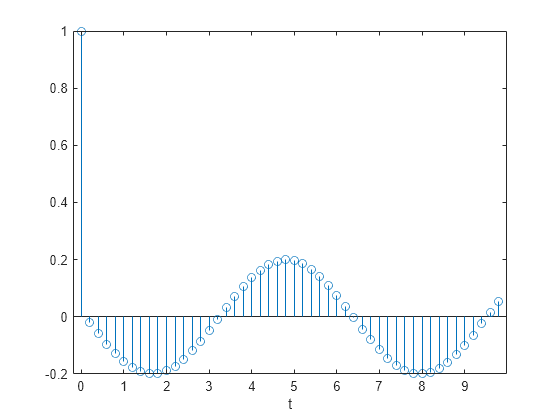
El sistema se estimula mediante un impulso unitario en sentido positivo. Calcule la evolución temporal del sistema utilizando la función de transferencia. Represente el resultado.

bf = [1 -(1+cos(dt)) cos(dt)];
af = [1 -2*cos(dt) 1];
yf = filter(bf,af,u);

stem(t,yf,"o")
xlabel("t")

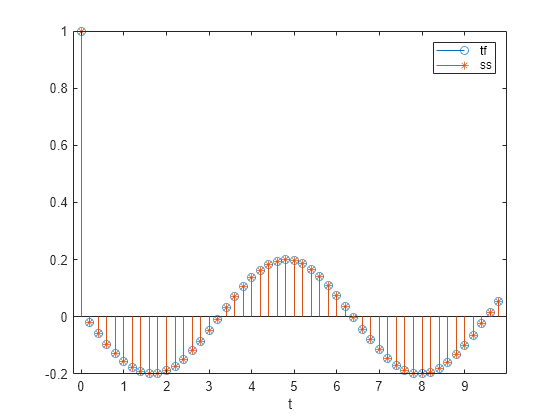
Busque la representación del espacio de estados del sistema. Calcule la evolución temporal partiendo de un estado inicial totalmente nulo. Compárelo con la predicción de la función de transferencia.

[A,B,C,D] = tf2ss(bf,af);

x = [0;0];
for k = 1:N
    y(k) = C*x + D*u(k);
    x = A*x + B*u(k);
end

hold on
stem(t,y,"*")
hold off
legend("tf","ss")

Argumentos de entrada

b — Coeficientes de la función de transferencia del numerador

vector | matriz

Coeficientes de numerador de función de transferencia, especificados como vector o matriz. Si b es una matriz, cada fila de b corresponde a una salida del sistema.

• Para los sistemas de tiempo discreto, b contiene los coeficientes en potencias descendentes de z.

• Para los sistemas de tiempo continuo, b contiene los coeficientes en potencias descendentes de s.

Para los sistemas de tiempo discreto, b debe tener un número de columnas igual a la longitud de a. Si los números difieren, iguálelos añadiendo ceros. Puede utilizar la función eqtflength para hacerlo.

a — Coeficientes de la función de transferencia del denominador

vector

Coeficientes de la función de transferencia del denominador, especificados como un vector.

• Para los sistemas de tiempo discreto, a contiene los coeficientes en potencias descendentes de z.

• Para los sistemas de tiempo continuo, a contiene los coeficientes en potencias descendentes de s.

Argumentos de salida

A — Matriz de estados

matriz

Matriz de estados, devuelta como una matriz. Si el sistema viene descrito por n variables de estado, A es n por n.

Tipos de datos: single | double

B — Matriz de entrada a estado

matriz

Matriz de entrada a estado, devuelta como una matriz. Si el sistema viene descrito por n variables de estado, B es n por 1.

Tipos de datos: single | double

C — Matriz de estado a salida

matriz

Matriz de estado a salida, devuelta como una matriz. Si el sistema tiene q salidas y está descrito por n variables de estado, C es q por n.

Tipos de datos: single | double

D — Matriz de alimentación

matriz

Matriz de alimentación, devuelta como una matriz. Si el sistema tiene q salidas, D es q por 1.

Tipos de datos: single | double

Más acerca de

Función de transferencia

tf2ss convierte los parámetros de una representación de la función de transferencia de un sistema dado en los de una representación equivalente del espacio de estados.

• Para los sistemas de tiempo discreto, las matrices del espacio de estados relacionan el vector de estados x, la entrada u y la salida y:

  $$\begin{array}{c}x\left(k+1\right)=Ax\left(k\right)+Bu\left(k\right),\\ y\left(k\right)=Cx\left(k\right)+Du\left(k\right).\end{array}$$

  La función de transferencia es la transformada Z de la respuesta al impulso. Se puede expresar en términos de matrices del espacio de estados como

  $$H\left(z\right)=C{\left(zI-A\right)}^{-1}B+D.$$

• Para los sistemas de tiempo continuo, las matrices del espacio de estados relacionan el vector de estados x, la entrada u y la salida y:

  $$\begin{array}{l}\dot{x}=Ax+Bu,\\ y=Cx+Du.\end{array}$$

  La función de transferencia es la transformada de Laplace de la respuesta al impulso. Se puede expresar en términos de matrices del espacio de estados como

  $$H(s)=\frac{B(s)}{A(s)}=\frac{b_1{s}^{n-1}+\cdots +b_{n-1}s+b_n}{a_1{s}^{m-1}+\cdots +a_{m-1}s+a_m}=C{\left(sI-A\right)}^{-1}B+D.$$

Capacidades ampliadas

Generación de código C/C++
Genere código C y C++ mediante MATLAB® Coder™.

Historial de versiones

Introducido antes de R2006a

Consulte también

sos2ss | ss2tf | tf2sos | tf2zp | tf2zpk | zp2ss