ss2tf

Convert state-space representation to transfer function

Syntax

[b,a] = ss2tf(A,B,C,D)

[b,a] = ss2tf(A,B,C,D,ni)

Description

[b,a] = ss2tf(A,B,C,D) converts a state-space representation of a system into an equivalent transfer function. ss2tf returns the Laplace-transform transfer function for continuous-time systems and the Z-transform transfer function for discrete-time systems.

[b,a] = ss2tf(A,B,C,D,ni) returns the transfer function that results when the nith input of a system with multiple inputs is excited by a unit impulse.

Examples

Mass-Spring System

A one-dimensional discrete-time oscillating system consists of a unit mass, $$m$$, attached to a wall by a spring of unit elastic constant. A sensor samples the acceleration, $$a$$, of the mass at $$F_s=5$$ Hz.

Generate 50 time samples. Define the sampling interval $$\Delta t=1/F_s$$.

Fs = 5;
dt = 1/Fs;
N = 50;
t = dt*(0:N-1);

The oscillator can be described by the state-space equations

$$\begin{array}{c}x(k+1)=Ax(k)+Bu(k),\\ y(k)=Cx(k)+Du(k),\end{array}$$

where $$x={\left(\begin{array}{cc}r& v\end{array}\right)}^T$$ is the state vector, $$r$$ and $$v$$ are respectively the position and velocity of the mass, and the matrices

$$A=\left(\begin{array}{cc}\cos \Delta t& \sin \Delta t\\ -\sin \Delta t& \cos \Delta t\end{array}\right),B=\left(\begin{array}{c}1-\cos \Delta t\\ \sin \Delta t\end{array}\right),C=\left(\begin{array}{cc}-1& 0\end{array}\right),D=\left(\begin{array}{c}1\end{array}\right).$$

A = [cos(dt) sin(dt);-sin(dt) cos(dt)];
B = [1-cos(dt);sin(dt)];
C = [-1 0];
D = 1;

The system is excited with a unit impulse in the positive direction. Use the state-space model to compute the time evolution of the system starting from an all-zero initial state.

u = [1 zeros(1,N-1)];

x = [0;0];
for k = 1:N
    y(k) = C*x + D*u(k);
    x = A*x + B*u(k);
end

Plot the acceleration of the mass as a function of time.

stem(t,y,'filled')
xlabel('t')

Compute the time-dependent acceleration using the transfer function H(z) to filter the input. Plot the result.

[b,a] = ss2tf(A,B,C,D);
yt = filter(b,a,u);

stem(t,yt,'filled')
xlabel('t')

The transfer function of the system has an analytic expression:

$$H(z)=\frac{1-z^{-1}(1+\cos \Delta t)+z^{-2}\cos \Delta t}{1-2z^{-1}\cos \Delta t+z^{-2}}.$$

Use the expression to filter the input. Plot the response.

bf = [1 -(1+cos(dt)) cos(dt)];
af = [1 -2*cos(dt) 1];
yf = filter(bf,af,u);

stem(t,yf,'filled')
xlabel('t')

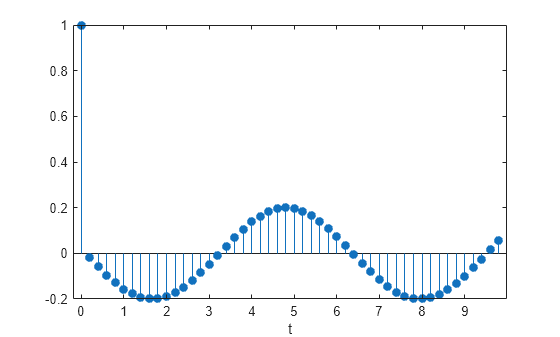
The result is the same in all three cases.

Two-Body Oscillator

An ideal one-dimensional oscillating system consists of two unit masses, $$m_1$$ and $$m_2$$, confined between two walls. Each mass is attached to the nearest wall by a spring of unit elastic constant. Another such spring connects the two masses. Sensors sample $$a_1$$ and $$a_2$$, the accelerations of the masses, at $$F_s=16$$ Hz.

Specify a total measurement time of 16 s. Define the sampling interval $$\Delta t=1/F_s$$.

Fs = 16;
dt = 1/Fs;
N = 257;
t = dt*(0:N-1);

The system can be described by the state-space model

$$\begin{array}{c}x(n+1)=Ax(n)+Bu(n),\\ y(n)=Cx(n)+Du(n),\end{array}$$

where $$x={\left(\begin{array}{cccc}{r}_1& v_1& r_2& v_2\end{array}\right)}^T$$ is the state vector and $$r_i$$ and $$v_i$$ are respectively the location and the velocity of the $$i$$th mass. The input vector $$u={\left(\begin{array}{cc}{u}_1& u_2\end{array}\right)}^T$$ and the output vector $$y={\left(\begin{array}{cc}{a}_1& a_2\end{array}\right)}^T$$. The state-space matrices are

$$A=\exp (A_c\Delta t),B=A_c^{-1}(A-I)B_c,C=\left(\begin{array}{cccc}-2& 0& 1& 0\\ 1& 0& -2& 0\end{array}\right),D=I,$$

the continuous-time state-space matrices are

$$A_c=\left(\begin{array}{cccc}0& 1& 0& 0\\ -2& 0& 1& 0\\ 0& 0& 0& 1\\ 1& 0& -2& 0\end{array}\right),B_c=\left(\begin{array}{cc}0& 0\\ 1& 0\\ 0& 0\\ 0& 1\end{array}\right),$$

and $$I$$ denotes an identity matrix of the appropriate size.

Ac = [0 1 0 0; -2 0 1 0; 0 0 0 1; 1 0 -2 0];
A = expm(Ac*dt);
Bc = [0 0; 1 0; 0 0; 0 1];
B = Ac\(A-eye(4))*Bc;
C = [-2 0 1 0; 1 0 -2 0];
D = eye(2);

The first mass, $$m_1$$, receives a unit impulse in the positive direction.

ux = [1 zeros(1,N-1)];
u0 = zeros(1,N);
u = [ux;u0];

Use the model to compute the time evolution of the system starting from an all-zero initial state.

x = [0 0 0 0]';
y = zeros(2,N);

for k = 1:N
    y(:,k) = C*x + D*u(:,k);
    x = A*x + B*u(:,k);
end

Plot the accelerations of the two masses as functions of time.

stem(t,y','.')
xlabel('t')
legend('a_1','a_2')
title('Mass 1 Excited')
grid

Convert the system to its transfer function representation. Find the response of the system to a positive unit impulse excitation on the first mass.

[b1,a1] = ss2tf(A,B,C,D,1);
y1u1 = filter(b1(1,:),a1,ux);
y1u2 = filter(b1(2,:),a1,ux);

Plot the result. The transfer function gives the same response as the state-space model.

stem(t,[y1u1;y1u2]','.')
xlabel('t')
legend('a_1','a_2')
title('Mass 1 Excited')
grid

The system is reset to its initial configuration. Now the other mass, $$m_2$$, receives a unit impulse in the positive direction. Compute the time evolution of the system.

u = [u0;ux];

x = [0;0;0;0];
for k = 1:N
    y(:,k) = C*x + D*u(:,k);
    x = A*x + B*u(:,k);
end

Plot the accelerations. The responses of the individual masses are switched.

stem(t,y','.')
xlabel('t')
legend('a_1','a_2')
title('Mass 2 Excited')
grid

Find the response of the system to a positive unit impulse excitation on the second mass.

[b2,a2] = ss2tf(A,B,C,D,2);
y2u1 = filter(b2(1,:),a2,ux);
y2u2 = filter(b2(2,:),a2,ux);

Plot the result. The transfer function gives the same response as the state-space model.

stem(t,[y2u1;y2u2]','.')
xlabel('t')
legend('a_1','a_2')
title('Mass 2 Excited')
grid

Input Arguments

A — State matrix

matrix

State matrix, specified as a matrix. If the system has p inputs and q outputs and is described by n state variables, then A is n-by-n.

Data Types: single | double

B — Input-to-state matrix

matrix

Input-to-state matrix, specified as a matrix. If the system has p inputs and q outputs and is described by n state variables, then B is n-by-p.

Data Types: single | double

C — State-to-output matrix

matrix

State-to-output matrix, specified as a matrix. If the system has p inputs and q outputs and is described by n state variables, then C is q-by-n.

Data Types: single | double

D — Feedthrough matrix

matrix

Feedthrough matrix, specified as a matrix. If the system has p inputs and q outputs and is described by n state variables, then D is q-by-p.

Data Types: single | double

ni — Input index

1 (default) | integer scalar

Input index, specified as an integer scalar. If the system has p inputs, use ss2tf with a trailing argument ni = 1, …, p to compute the response to a unit impulse applied to the nith input.

Data Types: single | double

Output Arguments

b — Transfer function numerator coefficients

vector | matrix

Transfer function numerator coefficients, returned as a vector or matrix. If the system has p inputs and q outputs and is described by n state variables, then b is q-by-(n + 1) for each input. The coefficients are returned in descending powers of s or z.

a — Transfer function denominator coefficients

vector

Transfer function denominator coefficients, returned as a vector. If the system has p inputs and q outputs and is described by n state variables, then a is 1-by-(n + 1) for each input. The coefficients are returned in descending powers of s or z.

More About

Transfer Function

• For discrete-time systems, the state-space matrices relate the state vector x, the input u, and the output y through

  $$\begin{array}{c}x(k+1)=\text{A}x(k)+\text{B}u(k)\\ y(k)=\text{C}x(k)+\text{D}u(k).\end{array}$$

  The transfer function is the Z-transform of the system’s impulse response. It can be expressed in terms of the state-space matrices as

  $$\text{H}(z)\text{=C}{(z\text{I}-\text{A})}^{-1}\text{B}+\text{D}.$$

• For continuous-time systems, the state-space matrices relate the state vector x, the input u, and the output y through

  $$\begin{array}{l}\dot{x}=\text{A}x+\text{B}u\\ y=\text{C}x+\text{D}u.\end{array}$$

  The transfer function is the Laplace transform of the system’s impulse response. It can be expressed in terms of the state-space matrices as

  $$\text{H}(s)=\text{C}{(s\text{I}-\text{A})}^{-1}\text{B}+\text{D}.$$

Version History

Introduced before R2006a