La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

Ventana de Kaiser

La ventana de Kaiser es una aproximación a la ventana esferoidal prolata, para la que se maximiza la relación de energía del lóbulo principal y de energía del lóbulo lateral. En una ventana de Kaiser de una longitud concreta, el parámetro β controla la atenuación relativa del lóbulo lateral. En una β dada, la atenuación relativa del lóbulo lateral es fija con respecto a la longitud de la ventana. La instrucción kaiser(n,beta) calcula una ventana de Kaiser de longitud n con el parámetro beta.

Cuando aumenta β, la atenuación relativa del lóbulo lateral disminuye y la anchura del lóbulo principal aumenta. Esta captura de pantalla muestra cómo la atenuación relativa del lóbulo lateral se mantiene aproximadamente igual para un parámetro β fijo al cambiar la longitud.

En este ejemplo se muestran ejemplos de ventanas de Kaiser con una longitud de 50 y unos parámetros β de 1, 4 y 9.

Para crear estas ventanas de Kaiser utilizando la línea de comandos de MATLAB^®, escriba lo siguiente:

n = 50;
w1 = kaiser(n,1);
w2 = kaiser(n,4);
w3 = kaiser(n,9);
[W1,f] = freqz(w1/sum(w1),1,512,2);
[W2,f] = freqz(w2/sum(w2),1,512,2);
[W3,f] = freqz(w3/sum(w3),1,512,2);
plot(f,20*log10(abs([W1 W2 W3])))
grid
legend('\beta = 1','\beta = 4','\beta = 9')

Para crear estas ventanas de Kaiser utilizando la línea de comandos de MATLAB, escriba lo siguiente:

w1 = kaiser(50,4);
w2 = kaiser(20,4);
w3 = kaiser(101,4);
[W1,f] = freqz(w1/sum(w1),1,512,2);
[W2,f] = freqz(w2/sum(w2),1,512,2);
[W3,f] = freqz(w3/sum(w3),1,512,2);
plot(f,20*log10(abs([W1 W2 W3])))
grid
legend('length = 50','length = 20','length = 101')

Ventanas de Kaiser en diseño FIR

Estas son dos fórmulas de diseño que pueden ayudarle a diseñar filtros FIR para cumplir una serie de especificaciones de filtro utilizando una ventana de Kaiser. Para lograr una atenuación relativa del lóbulo lateral de –α dB, el parámetro β (beta) es

$$\beta =\{\begin{array}{cc}0.1102\left(\alpha -8.7\right),& \alpha >50,\\ 0.5842{\left(\alpha -21\right)}^{0.4}+0.07886\left(\alpha -21\right),& 50\ge \alpha \ge 21,\\ 0,& \alpha <21.\end{array}$$

En una anchura de transición de $\Delta \omega$ rad/muestra, utilice la longitud

$$n=\frac{\alpha -8}{2.285\Delta \omega }+1$$.

Los filtros diseñados utilizando esta heurística cumplirán las especificaciones de forma aproximada, pero debe verificarlo. Para diseñar un filtro paso bajo con frecuencia de corte de 0,5$\pi$ rad/muestra, anchura de transición de 0,2$\pi$ rad/muestra y 40 dB de atenuación en la banda de parada, pruebe

[n,wn,beta] = kaiserord([0.4 0.6]*pi,[1 0],[0.01 0.01],2*pi);
h = fir1(n,wn,kaiser(n+1,beta),'noscale');

La función kaiserord estima el orden de filtro, la frecuencia de corte y el parámetro beta de la ventana de Kaiser necesarios para cumplir una serie de especificaciones de dominio de frecuencia.

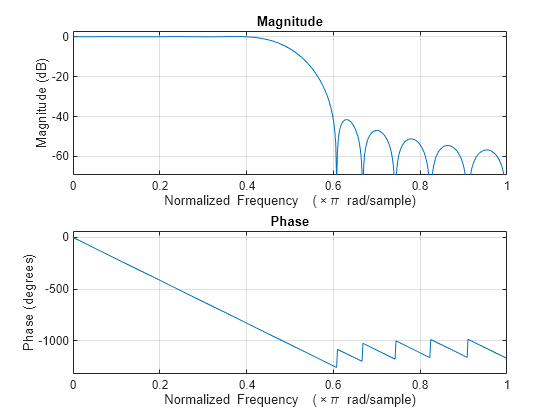
La ondulación en la banda de paso es aproximadamente la misma que la ondulación en la banda de parada. Como puede ver en la respuesta en frecuencia, este filtro casi cumple las especificaciones:

fvtool(h,1)

Consulte también

Apps

• Window Designer

Funciones

• freqz | kaiser | kaiserord | WVTool