kfoldPredict

Classify observations in cross-validated linear classification model

Syntax

Label = kfoldPredict(CVMdl)

[Label,Score] = kfoldPredict(CVMdl)

Description

Label = kfoldPredict(CVMdl) returns cross-validated class labels predicted by the cross-validated, binary, linear classification model CVMdl. That is, for every fold, kfoldPredict predicts class labels for observations that it holds out when it trains using all other observations.

Label contains predicted class labels for each regularization strength in the linear classification models that compose CVMdl.

[Label,Score] = kfoldPredict(CVMdl) also returns cross-validated classification scores for both classes. Score contains classification scores for each regularization strength in CVMdl.

Examples

Predict k-fold Cross-Validation Labels

Load the NLP data set.

load nlpdata

X is a sparse matrix of predictor data, and Y is a categorical vector of class labels. There are more than two classes in the data.

The models should identify whether the word counts in a web page are from the Statistics and Machine Learning Toolbox™ documentation. So, identify the labels that correspond to the Statistics and Machine Learning Toolbox™ documentation web pages.

Ystats = Y == 'stats';

Cross-validate a binary, linear classification model using the entire data set, which can identify whether the word counts in a documentation web page are from the Statistics and Machine Learning Toolbox™ documentation.

rng(1); % For reproducibility 
CVMdl = fitclinear(X,Ystats,'CrossVal','on');
Mdl1 = CVMdl.Trained{1}

Mdl1 = 
  ClassificationLinear
      ResponseName: 'Y'
        ClassNames: [0 1]
    ScoreTransform: 'none'
              Beta: [34023x1 double]
              Bias: -1.0008
            Lambda: 3.5193e-05
           Learner: 'svm'

CVMdl is a ClassificationPartitionedLinear model. By default, the software implements 10-fold cross validation. You can alter the number of folds using the 'KFold' name-value pair argument.

Predict labels for the observations that fitclinear did not use in training the folds.

label = kfoldPredict(CVMdl);

Because there is one regularization strength in Mdl1, label is a column vector of predictions containing as many rows as observations in X.

Construct a confusion matrix.

ConfusionTrain = confusionchart(Ystats,label);

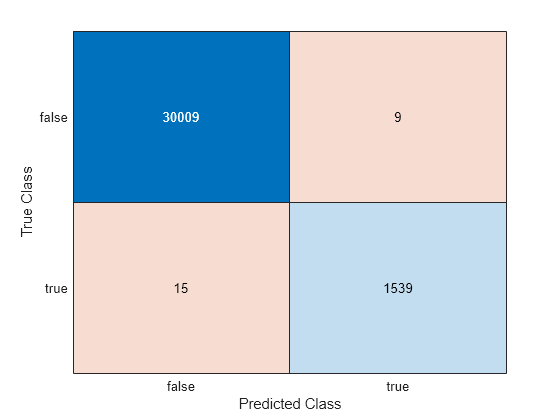
The model misclassifies 15 'stats' documentation pages as being outside of the Statistics and Machine Learning Toolbox documentation, and misclassifies nine pages as 'stats' pages.

Estimate k-fold Cross-Validation Posterior Class Probabilities

Linear classification models return posterior probabilities for logistic regression learners only.

Load the NLP data set and preprocess it as in Predict k-fold Cross-Validation Labels. Transpose the predictor data matrix.

load nlpdata
Ystats = Y == 'stats';
X = X';

Cross-validate binary, linear classification models using 5-fold cross-validation. Optimize the objective function using SpaRSA. Lower the tolerance on the gradient of the objective function to 1e-8.

rng(10); % For reproducibility
CVMdl = fitclinear(X,Ystats,'ObservationsIn','columns',...
    'KFold',5,'Learner','logistic','Solver','sparsa',...
    'Regularization','lasso','GradientTolerance',1e-8);

Predict the posterior class probabilities for observations not used to train each fold.

[~,posterior] = kfoldPredict(CVMdl);
CVMdl.ClassNames

ans = 2x1 logical array

   0
   1

Because there is one regularization strength in CVMdl, posterior is a matrix with 2 columns and rows equal to the number of observations. Column i contains posterior probabilities of Mdl.ClassNames(i) given a particular observation.

Compute the performance metrics (true positive rates and false positive rates) for a ROC curve and find the area under the ROC curve (AUC) value by creating a rocmetrics object.

rocObj = rocmetrics(Ystats,posterior,CVMdl.ClassNames);

Plot the ROC curve for the second class by using the plot function of rocmetrics.

plot(rocObj,ClassNames=CVMdl.ClassNames(2))

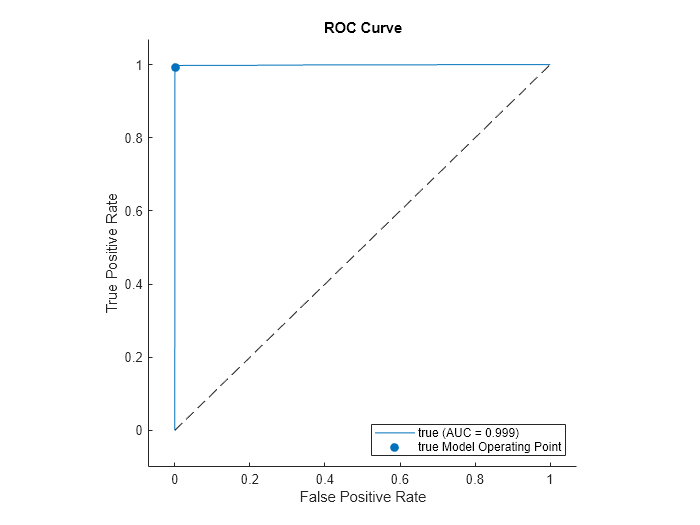
The ROC curve indicates that the model classifies the validation observations almost perfectly.

Find Good Lasso Penalty Using Cross-Validated AUC

To determine a good lasso-penalty strength for a linear classification model that uses a logistic regression learner, compare cross-validated AUC values.

Load the NLP data set. Preprocess the data as in Estimate k-fold Cross-Validation Posterior Class Probabilities.

load nlpdata
Ystats = Y == 'stats';
X = X';

There are 9471 observations in the test sample.

Create a set of 11 logarithmically-spaced regularization strengths from $$10^{-6}$$ through $$10^{-0.5}$$.

Lambda = logspace(-6,-0.5,11);

Cross-validate a binary, linear classification models that use each of the regularization strengths and 5-fold cross-validation. Optimize the objective function using SpaRSA. Lower the tolerance on the gradient of the objective function to 1e-8.

rng(10) % For reproducibility
CVMdl = fitclinear(X,Ystats,'ObservationsIn','columns', ...
    'KFold',5,'Learner','logistic','Solver','sparsa', ...
    'Regularization','lasso','Lambda',Lambda,'GradientTolerance',1e-8)

CVMdl = 
  ClassificationPartitionedLinear
    CrossValidatedModel: 'Linear'
           ResponseName: 'Y'
        NumObservations: 31572
                  KFold: 5
              Partition: [1x1 cvpartition]
             ClassNames: [0 1]
         ScoreTransform: 'none'

Mdl1 = CVMdl.Trained{1}

Mdl1 = 
  ClassificationLinear
      ResponseName: 'Y'
        ClassNames: [0 1]
    ScoreTransform: 'logit'
              Beta: [34023x11 double]
              Bias: [-13.2936 -13.2936 -13.2936 -13.2936 -13.2936 -6.8954 -5.4359 -4.7170 -3.4108 -3.1566 -2.9792]
            Lambda: [1.0000e-06 3.5481e-06 1.2589e-05 4.4668e-05 1.5849e-04 5.6234e-04 0.0020 0.0071 0.0251 0.0891 0.3162]
           Learner: 'logistic'

Mdl1 is a ClassificationLinear model object. Because Lambda is a sequence of regularization strengths, you can think of Mdl1 as 11 models, one for each regularization strength in Lambda.

Predict the cross-validated labels and posterior class probabilities.

[label,posterior] = kfoldPredict(CVMdl);
CVMdl.ClassNames;
[n,K,L] = size(posterior)

n = 
31572

K = 
2

L = 
11

posterior(3,1,5)

ans = 
1.0000

label is a 31572-by-11 matrix of predicted labels. Each column corresponds to the predicted labels of the model trained using the corresponding regularization strength. posterior is a 31572-by-2-by-11 matrix of posterior class probabilities. Columns correspond to classes and pages correspond to regularization strengths. For example, posterior(3,1,5) indicates that the posterior probability that the first class (label 0) is assigned to observation 3 by the model that uses Lambda(5) as a regularization strength is 1.0000.

For each model, compute the AUC by using rocmetrics.

auc = 1:numel(Lambda);  % Preallocation
for j = 1:numel(Lambda)
    rocObj = rocmetrics(Ystats,posterior(:,:,j),CVMdl.ClassNames);
    auc(j) = rocObj.AUC(1);
end

Higher values of Lambda lead to predictor variable sparsity, which is a good quality of a classifier. For each regularization strength, train a linear classification model using the entire data set and the same options as when you trained the model. Determine the number of nonzero coefficients per model.

Mdl = fitclinear(X,Ystats,'ObservationsIn','columns', ...
    'Learner','logistic','Solver','sparsa','Regularization','lasso', ...
    'Lambda',Lambda,'GradientTolerance',1e-8);
numNZCoeff = sum(Mdl.Beta~=0);

In the same figure, plot the test-sample error rates and frequency of nonzero coefficients for each regularization strength. Plot all variables on the log scale.

figure
yyaxis left
plot(log10(Lambda),log10(auc),'o-')
ylabel('log_{10} AUC')
yyaxis right
plot(log10(Lambda),log10(numNZCoeff + 1),'o-')
ylabel('log_{10} nonzero-coefficient frequency')
xlabel('log_{10} Lambda')
title('Cross-Validated Statistics')
hold off

Choose the index of the regularization strength that balances predictor variable sparsity and high AUC. In this case, a value between $$10^{-3}$$ to $$10^{-1}$$ should suffice.

idxFinal = 9;

Select the model from Mdl with the chosen regularization strength.

MdlFinal = selectModels(Mdl,idxFinal);

MdlFinal is a ClassificationLinear model containing one regularization strength. To estimate labels for new observations, pass MdlFinal and the new data to predict.

Input Arguments

CVMdl — Cross-validated, binary, linear classification model

ClassificationPartitionedLinear model object

Cross-validated, binary, linear classification model, specified as a ClassificationPartitionedLinear model object. You can create a ClassificationPartitionedLinear model using fitclinear and specifying any one of the cross-validation, name-value pair arguments, for example, CrossVal.

To obtain estimates, kfoldPredict applies the same data used to cross-validate the linear classification model (X and Y).

Output Arguments

Label — Cross-validated, predicted class labels

categorical array | character array | logical matrix | numeric matrix | cell array of character vectors

Cross-validated, predicted class labels, returned as a categorical or character array, logical or numeric matrix, or cell array of character vectors.

In most cases, Label is an n-by-L array of the same data type as the observed class labels (see Y) used to create CVMdl. (The software treats string arrays as cell arrays of character vectors.) n is the number of observations in the predictor data (see X) and L is the number of regularization strengths in CVMdl.Trained{1}.Lambda. That is, Label(i,j) is the predicted class label for observation i using the linear classification model that has regularization strength CVMdl.Trained{1}.Lambda(j).

If Y is a character array and L > 1, then Label is a cell array of class labels.

Score — Cross-validated classification scores

numeric array

Cross-validated classification scores, returned as an n-by-2-by-L numeric array. n is the number of observations in the predictor data that created CVMdl (see X) and L is the number of regularization strengths in CVMdl.Trained{1}.Lambda. Score(i,k,j) is the score for classifying observation i into class k using the linear classification model that has regularization strength CVMdl.Trained{1}.Lambda(j). CVMdl.ClassNames stores the order of the classes.

If CVMdl.Trained{1}.Learner is 'logistic', then classification scores are posterior probabilities.

More About

Classification Score

For linear classification models, the raw classification score for classifying the observation x, a row vector, into the positive class is defined by

$$f_j(x)=x{\beta }_j+b_j.$$

For the model with regularization strength j, $${\beta }_j$$ is the estimated column vector of coefficients (the model property Beta(:,j)) and $$b_j$$ is the estimated, scalar bias (the model property Bias(j)).

The raw classification score for classifying x into the negative class is –f(x). The software classifies observations into the class that yields the positive score.

If the linear classification model consists of logistic regression learners, then the software applies the 'logit' score transformation to the raw classification scores (see ScoreTransform).

Extended Capabilities

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced in R2016a

R2024a: Specify GPU arrays (requires Parallel Computing Toolbox)

kfoldPredict fully supports GPU arrays.

R2023b: Observations with missing predictor values are used in resubstitution and cross-validation computations

Starting in R2023b, the following classification model object functions use observations with missing predictor values as part of resubstitution ("resub") and cross-validation ("kfold") computations for classification edges, losses, margins, and predictions.

Model Type	Model Objects	Object Functions
Discriminant analysis classification model	ClassificationDiscriminant	resubEdge, resubLoss, resubMargin, resubPredict
	ClassificationPartitionedModel	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
Ensemble of discriminant analysis learners for classification	ClassificationEnsemble	resubEdge, resubLoss, resubMargin, resubPredict
	ClassificationPartitionedEnsemble	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
Gaussian kernel classification model	ClassificationPartitionedKernel	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
	ClassificationPartitionedKernelECOC	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
Linear classification model	ClassificationPartitionedLinear	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
	ClassificationPartitionedLinearECOC	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
Neural network classification model	ClassificationNeuralNetwork	resubEdge, resubLoss, resubMargin, resubPredict
	ClassificationPartitionedModel	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict
Support vector machine (SVM) classification model	ClassificationSVM	resubEdge, resubLoss, resubMargin, resubPredict
	ClassificationPartitionedModel	kfoldEdge, kfoldLoss, kfoldMargin, kfoldPredict

In previous releases, the software omitted observations with missing predictor values from the resubstitution and cross-validation computations.