kfoldMargin
Classification margins for observations not used in training
Description
m = kfoldMargin(CVMdl)CVMdl, which is a cross-validated, error-correcting
output codes (ECOC) model composed of linear classification models.
That is, for every fold, kfoldMargin estimates the
classification margins for observations that it holds out when it
trains using all other observations.
m contains classification margins for each
regularization strength in the linear classification models that comprise CVMdl.
m = kfoldMargin(CVMdl,Name,Value)Name,Value pair
arguments. For example, specify a decoding scheme or verbosity level.
Input Arguments
Cross-validated, ECOC model composed of linear classification
models, specified as a ClassificationPartitionedLinearECOC model
object. You can create a ClassificationPartitionedLinearECOC model
using fitcecoc and by:
Specifying any one of the cross-validation, name-value pair arguments, for example,
CrossValSetting the name-value pair argument
Learnersto'linear'or a linear classification model template returned bytemplateLinear
To obtain estimates, kfoldMargin applies the same data used
to cross-validate the ECOC model (X and Y).
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Binary learner loss function, specified as the comma-separated
pair consisting of 'BinaryLoss' and a built-in loss function name or function handle.
This table contains names and descriptions of the built-in functions, where yj is the class label for a particular binary learner (in the set {-1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss formula.
Value Description Score Domain g(yj,sj) "binodeviance"Binomial deviance (–∞,∞) log[1 + exp(–2yjsj)]/[2log(2)] "exponential"Exponential (–∞,∞) exp(–yjsj)/2 "hamming"Hamming [0,1] or (–∞,∞) [1 – sign(yjsj)]/2 "hinge"Hinge (–∞,∞) max(0,1 – yjsj)/2 "linear"Linear (–∞,∞) (1 – yjsj)/2 "logit"Logistic (–∞,∞) log[1 + exp(–yjsj)]/[2log(2)] "quadratic"Quadratic [0,1] [1 – yj(2sj – 1)]2/2 The software normalizes the binary losses such that the loss is 0.5 when yj = 0. Also, the software calculates the mean binary loss for each class.
For a custom binary loss function, e.g.,
customFunction, specify its function handle'BinaryLoss',@customFunction.customFunctionshould have this formwhere:bLoss = customFunction(M,s)
Mis the K-by-B coding matrix stored inMdl.CodingMatrix.sis the 1-by-B row vector of classification scores.bLossis the classification loss. This scalar aggregates the binary losses for every learner in a particular class. For example, you can use the mean binary loss to aggregate the loss over the learners for each class.K is the number of classes.
B is the number of binary learners.
For an example of passing a custom binary loss function, see Predict Test-Sample Labels of ECOC Model Using Custom Binary Loss Function.
By default, if all binary learners are linear classification models using:
SVM, then
BinaryLossis'hinge'Logistic regression, then
BinaryLossis'quadratic'
Example: 'BinaryLoss','binodeviance'
Data Types: char | string | function_handle
Decoding scheme that aggregates the binary losses, specified as the comma-separated pair
consisting of 'Decoding' and 'lossweighted' or
'lossbased'. For more information, see Binary Loss.
Example: 'Decoding','lossbased'
Estimation options, specified as a structure array as returned by statset.
To invoke parallel computing you need a Parallel Computing Toolbox™ license.
Example: Options=statset(UseParallel=true)
Data Types: struct
Verbosity level, specified as 0 or 1.
Verbose controls the number of diagnostic messages that the
software displays in the Command Window.
If Verbose is 0, then the software does not display
diagnostic messages. Otherwise, the software displays diagnostic messages.
Example: Verbose=1
Data Types: single | double
Output Arguments
Cross-validated classification margins, returned as a numeric vector or matrix.
m is n-by-L,
where n is the number of observations in X and L is
the number of regularization strengths in Mdl (that
is, numel(Mdl.Lambda)).
m( is
the cross-validated classification margin of observation i using
the ECOC model, composed of linear classification models, that has
regularization strength i,j)Mdl.Lambda(.j)
Examples
Load the NLP data set.
load nlpdataX is a sparse matrix of predictor data, and Y is a categorical vector of class labels.
For simplicity, use the label 'others' for all observations in Y that are not 'simulink', 'dsp', or 'comm'.
Y(~(ismember(Y,{'simulink','dsp','comm'}))) = 'others';Cross-validate a multiclass, linear classification model.
rng(1); % For reproducibility CVMdl = fitcecoc(X,Y,'Learner','linear','CrossVal','on');
CVMdl is a ClassificationPartitionedLinearECOC model. By default, the software implements 10-fold cross validation. You can alter the number of folds using the 'KFold' name-value pair argument.
Estimate the k-fold margins.
m = kfoldMargin(CVMdl); size(m)
ans = 1×2
31572 1
m is a 31572-by-1 vector. m(j) is the average of the out-of-fold margins for observation j.
Plot the k-fold margins using box plots.
figure;
boxplot(m);
h = gca;
h.YLim = [-5 5];
title('Distribution of Cross-Validated Margins')
One way to perform feature selection is to compare k-fold margins from multiple models. Based solely on this criterion, the classifier with the larger margins is the better classifier.
Load the NLP data set. Preprocess the data as in Estimate k-Fold Cross-Validation Margins, and orient the predictor data so that observations correspond to columns.
load nlpdata Y(~(ismember(Y,{'simulink','dsp','comm'}))) = 'others'; X = X';
Create these two data sets:
fullXcontains all predictors.partXcontains 1/2 of the predictors chosen at random.
rng(1); % For reproducibility p = size(X,1); % Number of predictors halfPredIdx = randsample(p,ceil(0.5*p)); fullX = X; partX = X(halfPredIdx,:);
Create a linear classification model template that specifies optimizing the objective function using SpaRSA.
t = templateLinear('Solver','sparsa');
Cross-validate two ECOC models composed of binary, linear classification models: one that uses the all of the predictors and one that uses half of the predictors. Indicate that observations correspond to columns.
CVMdl = fitcecoc(fullX,Y,'Learners',t,'CrossVal','on',... 'ObservationsIn','columns'); PCVMdl = fitcecoc(partX,Y,'Learners',t,'CrossVal','on',... 'ObservationsIn','columns');
CVMdl and PCVMdl are ClassificationPartitionedLinearECOC models.
Estimate the k-fold margins for each classifier. Plot the distribution of the k-fold margins sets using box plots.
fullMargins = kfoldMargin(CVMdl); partMargins = kfoldMargin(PCVMdl); figure; boxplot([fullMargins partMargins],'Labels',... {'All Predictors','Half of the Predictors'}); h = gca; h.YLim = [-1 1]; title('Distribution of Cross-Validated Margins')
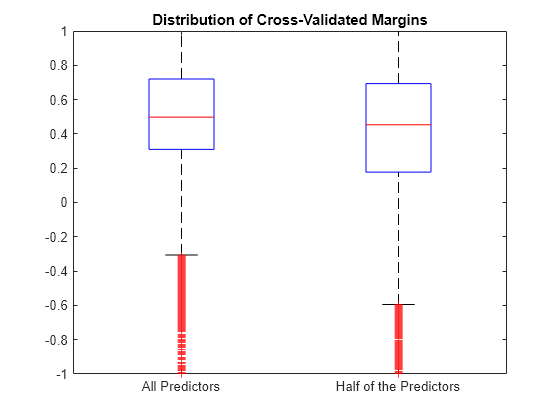
The distributions of the k-fold margins of the two classifiers are similar.
To determine a good lasso-penalty strength for a linear classification model that uses a logistic regression learner, compare distributions of k-fold margins.
Load the NLP data set. Preprocess the data as in Feature Selection Using k-fold Margins.
load nlpdata Y(~(ismember(Y,{'simulink','dsp','comm'}))) = 'others'; X = X';
Create a set of 11 logarithmically-spaced regularization strengths from through .
Lambda = logspace(-8,1,11);
Create a linear classification model template that specifies using logistic regression with a lasso penalty, using each of the regularization strengths, optimizing the objective function using SpaRSA, and reducing the tolerance on the gradient of the objective function to 1e-8.
t = templateLinear('Learner','logistic','Solver','sparsa',... 'Regularization','lasso','Lambda',Lambda,'GradientTolerance',1e-8);
Cross-validate an ECOC model composed of binary, linear classification models using 5-fold cross-validation and that
rng(10); % For reproducibility CVMdl = fitcecoc(X,Y,'Learners',t,'ObservationsIn','columns','KFold',5)
CVMdl =
ClassificationPartitionedLinearECOC
CrossValidatedModel: 'LinearECOC'
ResponseName: 'Y'
NumObservations: 31572
KFold: 5
Partition: [1×1 cvpartition]
ClassNames: [comm dsp simulink others]
ScoreTransform: 'none'
Properties, Methods
CVMdl is a ClassificationPartitionedLinearECOC model.
Estimate the k-fold margins for each regularization strength. The scores for logistic regression are in [0,1]. Apply the quadratic binary loss.
m = kfoldMargin(CVMdl,'BinaryLoss','quadratic'); size(m)
ans = 1×2
31572 11
m is a 31572-by-11 matrix of cross-validated margins for each observation. The columns correspond to the regularization strengths.
Plot the k-fold margins for each regularization strength.
figure; boxplot(m) ylabel('Cross-validated margins') xlabel('Lambda indices')

Several values of Lambda yield similarly high margin distribution centers with low spreads. Higher values of Lambda lead to predictor variable sparsity, which is a good quality of a classifier.
Choose the regularization strength that occurs just before the margin distribution center starts decreasing and spread starts increasing.
LambdaFinal = Lambda(5);
Train an ECOC model composed of linear classification model using the entire data set and specify the regularization strength LambdaFinal.
t = templateLinear('Learner','logistic','Solver','sparsa',... 'Regularization','lasso','Lambda',Lambda(5),'GradientTolerance',1e-8); MdlFinal = fitcecoc(X,Y,'Learners',t,'ObservationsIn','columns');
To estimate labels for new observations, pass MdlFinal and the new data to predict.
More About
The binary loss is a function of the class and classification score that determines how well a binary learner classifies an observation into the class. The decoding scheme of an ECOC model specifies how the software aggregates the binary losses and determines the predicted class for each observation.
Assume the following:
mkj is element (k,j) of the coding design matrix M—that is, the code corresponding to class k of binary learner j. M is a K-by-B matrix, where K is the number of classes, and B is the number of binary learners.
sj is the score of binary learner j for an observation.
g is the binary loss function.
is the predicted class for the observation.
The software supports two decoding schemes:
Loss-based decoding [2] (
Decodingis"lossbased") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over all binary learners.Loss-weighted decoding [3] (
Decodingis"lossweighted") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over the binary learners for the corresponding class.The denominator corresponds to the number of binary learners for class k. [1] suggests that loss-weighted decoding improves classification accuracy by keeping loss values for all classes in the same dynamic range.
The predict, resubPredict, and
kfoldPredict functions return the negated value of the objective
function of argmin as the second output argument
(NegLoss) for each observation and class.
This table summarizes the supported binary loss functions, where yj is a class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss function.
| Value | Description | Score Domain | g(yj,sj) |
|---|---|---|---|
"binodeviance" | Binomial deviance | (–∞,∞) | log[1 + exp(–2yjsj)]/[2log(2)] |
"exponential" | Exponential | (–∞,∞) | exp(–yjsj)/2 |
"hamming" | Hamming | [0,1] or (–∞,∞) | [1 – sign(yjsj)]/2 |
"hinge" | Hinge | (–∞,∞) | max(0,1 – yjsj)/2 |
"linear" | Linear | (–∞,∞) | (1 – yjsj)/2 |
"logit" | Logistic | (–∞,∞) | log[1 + exp(–yjsj)]/[2log(2)] |
"quadratic" | Quadratic | [0,1] | [1 – yj(2sj – 1)]2/2 |
The software normalizes binary losses so that the loss is 0.5 when yj = 0, and aggregates using the average of the binary learners [1].
Do not confuse the binary loss with the overall classification loss (specified by the
LossFun name-value argument of the kfoldLoss and
kfoldPredict object functions), which measures how well an ECOC
classifier performs as a whole.
The classification margin is, for each observation, the difference between the negative loss for the true class and the maximal negative loss among the false classes. If the margins are on the same scale, then they serve as a classification confidence measure. Among multiple classifiers, those that yield greater margins are better.
References
[1] Allwein, E., R. Schapire, and Y. Singer. “Reducing multiclass to binary: A unifying approach for margin classifiers.” Journal of Machine Learning Research. Vol. 1, 2000, pp. 113–141.
[2] Escalera, S., O. Pujol, and P. Radeva. “Separability of ternary codes for sparse designs of error-correcting output codes.” Pattern Recog. Lett. Vol. 30, Issue 3, 2009, pp. 285–297.
[3] Escalera, S., O. Pujol, and P. Radeva. “On the decoding process in ternary error-correcting output codes.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 32, Issue 7, 2010, pp. 120–134.
Extended Capabilities
To run in parallel, specify the Options name-value argument in the call to
this function and set the UseParallel field of the
options structure to true using
statset:
Options=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2016aStarting in R2023b, the following classification model object functions use observations with missing predictor values as part of resubstitution ("resub") and cross-validation ("kfold") computations for classification edges, losses, margins, and predictions.
In previous releases, the software omitted observations with missing predictor values from the resubstitution and cross-validation computations.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)