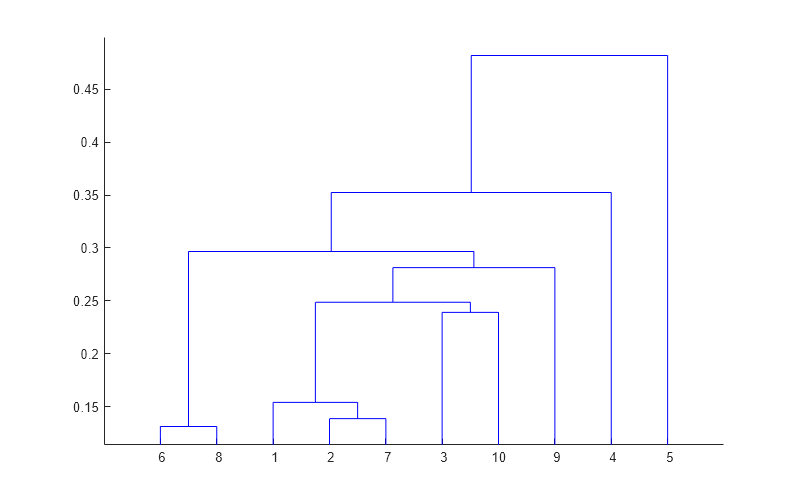
inconsistent
Inconsistency coefficient
Description
Y = inconsistent(Z)Z generated by the linkage function. inconsistent calculates the
inconsistency coefficient for each link by comparing its height with the average
height of other links at the same level of the hierarchy. The larger the
coefficient, the greater the difference between the objects connected by the link.
For more information, see Algorithms.
Examples
Input Arguments
Output Arguments
Algorithms
For each link k, the inconsistency coefficient is calculated as
where Y is the inconsistency coefficient
information for links in the hierarchical cluster tree Z.
For links that have no further links below them, the inconsistency coefficient is set to 0.
References
[1] Jain, A., and R. Dubes. Algorithms for Clustering Data. Upper Saddle River, NJ: Prentice-Hall, 1988.
[2] Zahn, C. T. “Graph-theoretical methods for detecting and describing Gestalt clusters.” IEEE Transactions on Computers. Vol. C-20, Issue 1, 1971, pp. 68–86.
Version History
Introduced before R2006a