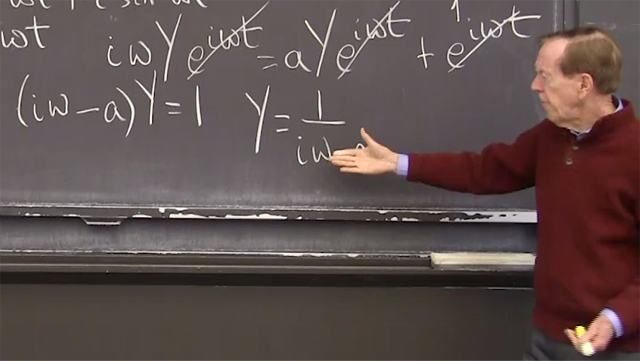Differential Equations and Linear Algebra, 1.6b: Integrating Factor for a Varying Rate, a(t)
From the series: Differential Equations and Linear Algebra
Gilbert Strang, Massachusetts Institute of Technology (MIT)
The integral of a varying interest rate provides the exponent in the growing solution (the bank balance).
Published: 27 Jan 2016
OK? I want to talk about a slightly different way to solve a linear first-order equation. And if you look at the equation-- I'll do an example. That's the best. Do you notice what's different from our favorite equation? The change is 2t. The interest rate a is increasing with time, changing with time. So we still have a linear equation, still just y. But the coefficient is varying. We have a variable coefficient 2t.
And if we think here of applications to economy, to banks, that would be rampant inflation, the interest rate 2t climbing and climbing forever. But we want to see that this is a class of equations that we can solve. OK. And the new method is called an integrating factor. It's a magic factor that makes the equation simple. So that's another nice way to solve all the problems that we've dealt with so far, plus this new one.
So what is this factor? Well, for this 2t problem, the right factor is e to the minus t squared. And why is that the right factor? This is the factor that I'm going to multiply the equation by and make it simple. And the reason that's the right choice is that the derivative of this-- you remember how to take the derivative by the chain rule?
The derivative will be the same e to the minus t squared, the same I, times the derivative of the exponent. And the derivative of that exponent is minus 2t. Minus t squared becomes minus 2t. So it's that little device that gives us an integrating factor that makes the equation simple.
And now I'm going to look at the equation. What I want to look at is the derivative of I times y. Instead of just dy dt, let me look at the derivative of I times y. So I have a product here. Got to use the product rule. So that will be I-- so I dy dt. OK. dy dt is-- we can take dy dt from the equation, I times 2ty plus q of t. And now I have to add on dI dt y. Good.
So it's the product rule-- I times the derivative of y plus the derivative of I times y. But now look. dI dt we know is minus 2tI. So that dI dt, now I'm using the key fact about I, that that's minus 2tIy. Look, minus 2tIy cancels 2tIy. So I have a nice equation now. The derivative of Iy is Iq. The derivative of Iy is Iq. I can just integrate both sides. And that's the key. That's the key.
If I integrate the left-hand side-- so I'll just move this up-- integrate the derivative-- of course, the integral of the derivative is the function-- at time t, Iy at time t minus Iy at time 0, y of 0. Because notice that I at t equals 0-- can I just mention that-- I at 0 is 1. When t is 0, I of e to the 0 power, which is 1. So that I of 0 is 1. So that's the integral of the derivative.
And on the right-hand side, I have the integral from 0 to t of I times q. So I'll put in-- yeah, e to the minus s squared q of s ds. I've introduced a variable of integration s going from 0 to t. You remember this type of formula? The input is continuous over time, and I'm looking at the resulting output at time t. So all the inputs go in. They're all multiplied by some factor and integrated gives the total result from those inputs.
OK. I'm almost here. I just want to remember I want to divide by I of t so I have a formula for y. OK. So my formula for y. When I divide by I of t-- don't forget what I of t is. Let me put it again here. Let me remind myself. I of t is e to the minus t squared. That was the magic integrating factor.
OK. So I'm going to divide by that, which means I'll multiply by e to the t squared. So that will knock out the I here. I'll put this on the other side of the equation, y of 0, y of 0, and it will be multiplied by the e to the t squared. And this thing will be multiplied by e to the t squared. The integral from 0 to t of e to the t squared minus s squared q of s ds. That's my answer.
Well, let's look at it. I have y of t. This is what comes out of y of 0. You see that the growth factor has changed from our old e to the at-- that was the growth at constant rate, interest rate a-- to e to the t squared. That's our growth from an increasing interest rate.
And over here, I'm seeing the result, the output, from the input q, from all the inputs between 0 and t. Each input is multiplied by now that factor is the growth not from 0 to t. This is the growth from 0 to t. This is the growth from s to t, because the input went in at time s, and it had the shorter time, t minus s, to grow.
So that's the formula for the answer. If you give me any particular q of s, I just do the integral, and I find the solution to the differential equation. So that integrating factor has made things work.
Maybe I should say what the integrating factor would be in general. So let me take a moment to see-- this was an example. This was an example with a of t equal to 2t. What's the general integrating factor? So we always want the integrating factor. Our construction rule is that it should give us-- the derivative should be minus a of t times I itself. That's how we chose the e to the minus t squared. Then a of t was 2t.
Now I want to give the general rule. The general rule for the integrating factor is the solution to that equation. The solution to that equation is giving us the e to the t squared in the example. This was the example.
But now I want a formula just to close off the entire case of varying interest rate. I want to find the solution to that equation. And it is-- so here's the integrating factor. It's e to the minus because of that minus sign. Now I'm wanting a to come down when I take a derivative. So what I'll put up here, the integral of a of t dt, say, from 0 to t.
Now, let me just do again this example just to see. I have e to the minus the integral of 2t, which is e to minus t squared. That's how I get t squared as the right choice for our example. And the general rule is there. That's the integrating factor.
And finally, finally, if a is a constant, which is the most common case-- the only case we've had until this video-- if a is a constant, then the integral of a from 0 to t is just a times t. So number one example, number zero example, would be e to the minus at. That would be the correct integrating factor if we had constant a.
And I'll create some examples, some problems, just to go through the steps in that best case of all with constant integrating factor. But now we can solve it with a varying interest rate. Good. Thank you.