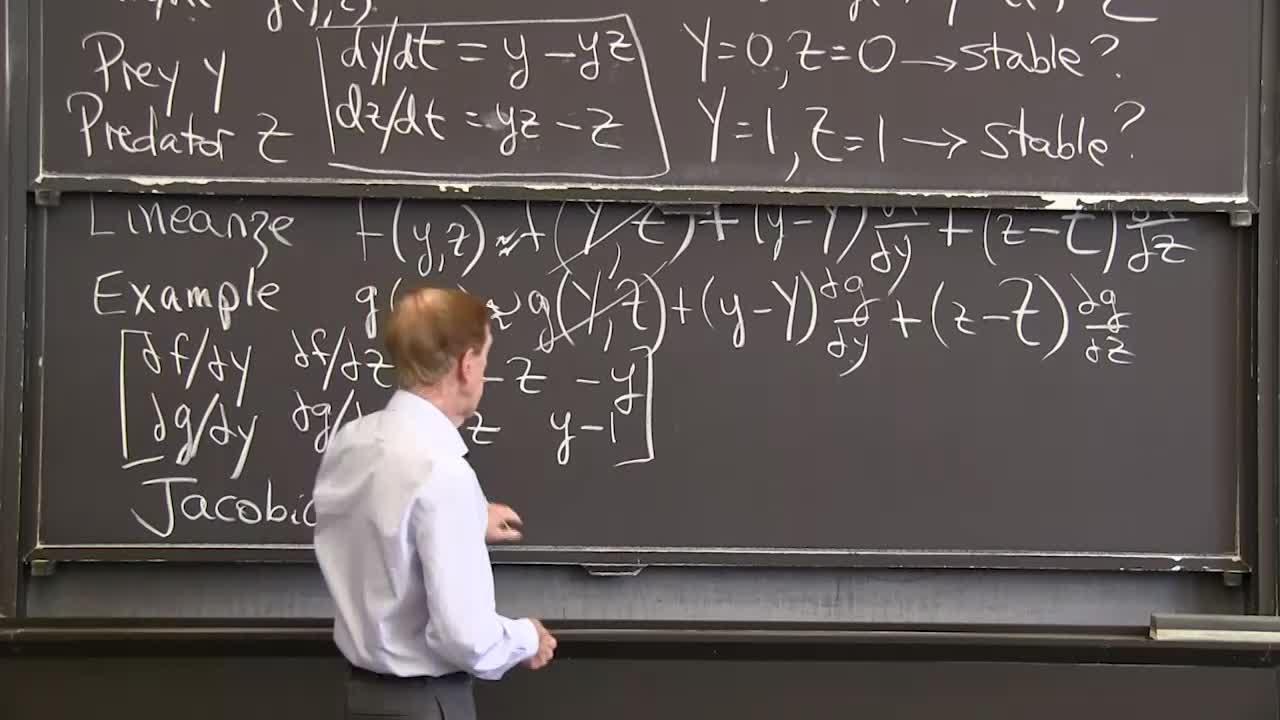Differential Equations and Linear Algebra, 3.3b: Linearization of y'=f(y,z) and z'=g(y,z)
From the series: Differential Equations and Linear Algebra
Gilbert Strang, Massachusetts Institute of Technology (MIT)
With two equations, a critical point has f(Y,Z) = 0 and g(Y,Z) = 0. Near those constant solutions, the two linearized equations use the 2 by 2 matrix of partial derivatives of f and g.
Published: 27 Jan 2016
OK. Two equations, the question of stability for two equations, stability around a critical point. OK. So the idea will be to linearize, to look very near that critical point, that point. But now we're in two dimensions. So that's a little more to do.
So here's the general picture, and then here is an example. So here's the general setup. We have an equation for the changes in y. But z is involved. And we have an equation for the rate of change of z. But y is involved. So they're coupled together. It's that coupling that's going to be new.
So what's a critical point? Critical point is when those right-hand sides are 0. Because then y and z are both constant. So they stay at that point. Wherever they are at this critical point is steady state. They stay steady. They stay steady. They stay at that constant value. So we want that to be 0. And we want this to be 0.
We have two equations, f equals 0, and g equals 0, two equations. But we have two unknowns, y and z. So we expect some solutions. And each solution has to be looked at separately. Each solution is a critical point. It's like well, you could think of a golf course, with a surface going up. So critical points will be points where the maximum point maybe, or the minimum point, or we'll see something called a saddle point.
Actually, let's do the example. The example is a famous one. Predator-prey it's known as. Predator like foxes, prey like rabbits. So the foxes eat the rabbits. And the question is, what are the steady states where foxes' and rabbits' constant values could stay?
So here this is the equation for what happens to the prey. So if the rabbits are left alone, the prey is the rabbits. If they're left alone they multiply, plenty of grass. Go for it. But if there are foxes, and z counts the number of foxes, then foxes eat, shall I say, those rabbits. And we lose rabbits. So we see that with a minus sign. And the amount of preying that goes on is proportional to the number of foxes times the number of rabbits. Because that gives the number of possible meetings.
And what about the foxes, the predator? The predator increases. So this is from encountering the rabbits. That tends to make the number of predators increase. But if there were no rabbits, the foxes don't eat grass. They're out of luck, and they decay. So I see a minus z there. So you see the pattern?
So starting from 0 and 0, at that point, so I've defined critical points. So there's my f. And that should be 0. And there is my g, and that should be 0. And it turns out there are just two possibilities.
This is one. If y and z are both 0, then certainly I would get 0's. So that's like starting with a very small number of foxes and rabbits. Or if y is 1 and z equal 1, do you see that that would be, they would be in perfect balance? If y is 1, and z is 1, then that's 0 and that's 0. So the equation is satisfied. We can stay at-- y can stay at 1, and z can stay at 1. It's a steady state. And the question is, is that steady state where rabbits are staying-- their population is staying at 1, because they're eating grass, good. But they're getting eaten by the foxes, bad. And those two balance, and give a rate of change of zero.
And the foxes similarly, the foxes get a positive push from eating rabbits. But natural causes cut them back. And they balance at z equal to 1.
OK. So what I have to do is linearize. And that's the real point of the lecture. That's the real point for linear-- how do linearize for two functions? And how do you linearize for these two functions? So let me-- I have to write the general formula first, so you'll see it. And then I'll apply it to those two functions. OK.
So here is the idea of linearize. So I'm linearizing. So my first function is whatever its value is at this point, it's like a tangent line. But now I've got two derivatives. Because the function depends on two variables. So I have a y minus capital Y, times now I have to do partial derivative. So that's the slope in the y direction, multiplied by the movement.
And then similar term, z minus capital Z times the movement in the z direction. And I have to, because I stopped, this is the linear part of the function. I have to put an approximate symbol. Because I've ignored higher derivatives. And of course this is 0. So that's why we have linear in y and linear in z, times some numbers, the slopes.
But we have two more slopes. Because we have another function g of y and z. And that again will just be approximately g at the critical point, which is 0 plus y minus capital Y, times dg dy plus z minus capital Z times dg dz. So altogether, the linear stuff and four numbers, the derivatives of f in the y and z directions, the derivatives of g in the y and the z directions. OK.
Now we had an example going. Let me bring that example down again. There was my f. There was my g. Can easily find those partial derivatives. So let me do it. So the partial derivative with respect to y will be 1 minus z, z held constant for that partial derivative. And the partial derivative with respect to z will be minus y. Let me write all those things down.
So here is in the example. So can I create a little matrix, df dy? It's the nice way, if I've got four things, 2 by 2 matrix is great. df, dz; that number, dg, dy; and dg dz. You could say this is the first derivative matrix. It's the matrix of first derivatives and it's always named after Jacobi who studied these first. So it's called the Jacobian matrix. Maybe I'll put his name to give him credit, Jacobi.
And the matrix is the Jacobian matrix. And its determinant is important. It's a very important matrix, important in economics. We're doing things-- I'm speaking here about predator-prey, little animals running around. But serious stuff is the economy. Is the economy stable? If it's a running along at some steady state and we move it a little bit, does it return to that steady state, or does it get totally out of hand?
So there is the Jacobian matrix. And what are those derivatives? Remember again, what functions. There's my functions. So the y derivative is 1 minus z. And the z derivative is minus y. The y derivative is z, and the z derivative is y minus 1. Is that all right? This is what we need to know from the functions. I've forgotten the functions in the board that went up. Here are their derivatives.
Now that's my Jacobian matrix. That's my matrix of the-- that matrix has these four coefficients, those four numbers. And really, so the linearization, let me call that matrix. I should call it J for Jacobian. I will call it J for Jacobian. OK. That's the Jacobian matrix.
So then my approximate-- what's my linearized equation? My linearized equation is the time derivative of y and z. So this left-hand side is just dy dt, and dz dt. So I'm using vector notations, putting y and z together, instead of separately, no big deal.
So then I have this matrix J, this 2 by 2 matrix, times you notice here is a y minus capital Y and a z minus capital Z. There is the linearized problem. Linearized because this is constant, and this is linear, single y, single z, and we have a matrix J.
So I have to find-- so now my little job is find the critical points. I've got everything ready. I have to find the critical points. Now remember, the critical points are where f and g are 0. And let me remember what those are. So there is the f. There's the g. One critical point was that one. Everything is 0. Another critical point is that one. Again, everything is 0. So I have two critical points, two Jacobian matrices, one at the first point, one at the second point.
So what are those matrices? At y and z equals 0, I have the matrix-- I'll put it here, and then I'll copy it. If y and z are 0, I have a 1 and a 0 and a 0 and a minus 1. I just took y and z to be 0. That was the first critical point. The second critical point gives me the Jacobian at that second point. The second point was when z was 1. So that's 0 now. And y was 1, so that's minus 1. z is a 1, y minus 1, y is a 1. So that's a 0. That's the second Jacobian.
So we're seeing something interesting here. We're seeing how 2 by 2 matrices will work by really nice examples, 1, 0, minus 1. What's that telling me? That's telling me that the rabbits grow. Because the rabbits are the first, the y. And the foxes decay. And that's what's happening when the two populations are really small. When the two populations are really small, multiplying them together is extremely small. So when the two populations are really small, forget the eating. There aren't enough people around, enough foxes and rabbits around to make a decent meal. So I just have dy dt equal y. Rabbits are growing from eating grass. dz dt is minus z, foxes are decaying from natural causes. So that's what kind of a stationary point will 0, 0 be?
Rabbits are growing. It's an unstable point. We're leaving at 0, 0. Rabbits are increasing. Now how about the second point? The second point was when they were both 1. when they're both 1, then we got this as the Jacobian matrix. Oh, this is the interesting one. Can I just stay with this one to finish? So I'm interested in the-- and I'll put these facts on a new board.
So again, y prime dy dt is y minus yz. z prime is yz, rabbits are getting eaten, minus z. And I'm interested in the point y equal 1, z equal 1. And my matrix of this is the Jacobian matrix. The Jacobian matrix had the derivatives, which were 1 minus z, minus y. The y derivative of that is z. The z derivative is y minus 1. And at this point y and z are 1. So that became 0, minus 1, 1 and 0.
And what kind of a problem do I have here? So my linearized equation, so linearized, linearized around the point 1,1. My equation is y minus 1 prime, sorry. It's the distance to the critical points. the derivative of y minus 1 is, I see here a minus 1. I see a minus z minus 1. And here a plus y minus 1.
You've got to understand this pair of linearized equations. If I use some other variable, the derivative of the first guy is minus the second. The derivative of the second guy is plus the first. What will happen?
Initially if I'm a little bit-- if I have extra foxes, the rabbit population will drop. The rabbit population-- this will be negative. If z, the number of foxes, is a little higher than 1, then the rabbit population drops. And when the rabbit population drops, z starts dropping. As z starts dropping below 1, the rabbit population starts increasing. I get, what shall we say, sort of exchange of rabbits and foxes, oscillation between rabbits and foxes?
So this is the-- right in the center there, that would be the point where y is 1 and z equal 1, the critical point. And if I start out with some extra rabbits, then the number of rabbits will drop. Because foxes are eating them. The number of foxes will increase. I'll go up. So there I have a little bit later, I have foxes now, but no rabbits to eat. So the foxes start dropping, and what happens?
I think, yeah. The number of rabbit starts increasing. And this is what happens. I'll go around and around in a circle. If you remember the pictures of the paths for 2 by 2 equations, there were saddle points. That's what this is. y equals 0, z equals 0 was a saddle point. So no, it's a saddle.
And what I'm discovering now for y equal 1 is an oscillation between foxes and rabbits. So again, I could say it'll be our center that was the very special picture where it didn't spiral out. It didn't spiral in. The special numbers, the eigenvalues of that matrix are-- well, better leave eigenvalues for the future. Because they happen to be i and minus i here.
It's motion in a circle. It comes from this, the equation here. Motion in a circle as in y double prime plus y equals 0. That's motion in a circle. And that's what we've got.
So this is a center. Now what about-- do I call a center stable? Not quite, because the rabbits and foxes don't approach 1. They stay on a circle around 1. Either I've got extra rabbits or extra foxes. But the total energy or the total stays a constant on that circle. And I would call that neutrally neutral. Neutral stability, because it doesn't blow up. I don't leave the area around. I stay close to the critical point. But I don't approach it either.
OK. So that's a case where we could see the stability, based on the linearization. OK. One more example to come in another lecture. Thanks.