La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

fminimax

Resolver un problema de restricción minimax

Sintaxis

x = fminimax(fun,x0)

x = fminimax(fun,x0,A,b)

x = fminimax(fun,x0,A,b,Aeq,beq)

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub)

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

x = fminimax(problem)

[x,fval] = fminimax(___)

[x,fval,maxfval,exitflag,output] = fminimax(___)

[x,fval,maxfval,exitflag,output,lambda] = fminimax(___)

Descripción

fminimax busca un punto que minimice el máximo de un conjunto de funciones objetivo.

El problema incluye cualquier tipo de restricción. En detalle, fminimax busca el mínimo de un problema especificado por

$$\underset{x}{\min }\underset{i}{\max }{F}_i(x)\text{ such that }\{\begin{array}{c}c(x)\le 0\\ ceq(x)=0\\ A\cdot x\le b\\ Aeq\cdot x=beq\\ lb\le x\le ub\end{array}$$

donde b y beq son vectores, A y Aeq son matrices y c(x), ceq(x) y F(x) son funciones que devuelven vectores. F(x), c(x) y ceq(x) pueden ser funciones no lineales.

x, lb y ub se pueden pasar como vectores o matrices; consulte Argumentos de matriz.

También se pueden resolver problemas max-min con fminimax, usando la identidad

$$\underset{x}{\max }\underset{i}{\min }{F}_i(x)=-\underset{x}{\min }\underset{i}{\max }\left(-F_i(x)\right).$$

Puede resolver problemas con el formato

$$\underset{x}{\min }\underset{i}{\max }\left|F_i(x)\right|$$

utilizando la opción AbsoluteMaxObjectiveCount; consulte Resolver un problema minimax utilizando el valor absoluto de un objetivo.

x = fminimax(fun,x0) comienza en x0 y encuentra una solución minimax x para las funciones descritas en fun.

Nota

En Pasar parámetros adicionales se explica cómo pasar parámetros adicionales a las funciones objetivo y a las funciones de restricción no lineales, si fuera necesario.

x = fminimax(fun,x0,A,b) resuelve el problema minimax sujeto a las desigualdades lineales A*x ≤ b.

x = fminimax(fun,x0,A,b,Aeq,beq) resuelve también el problema minimax sujeto a las igualdades lineales Aeq*x = beq. Si no existen desigualdades, establezca A = [] y b = [].

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub) resuelve el problema minimax sujeto a los límites lb ≤ x ≤ ub. Si no existen igualdades, establezca Aeq = [] y beq = []. Si x(i) está desacotado por abajo, establezca lb(i) = –Inf; si x(i) está desacotado por arriba, establezca ub(i) = Inf.

Nota

Consulte Las iteraciones pueden vulnerar las restricciones.

Nota

Si los límites de entrada especificados para un problema son inconsistentes, la salida x es x0 y la salida fval es [].

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) resuelve el problema minimax sujeto a las desigualdades no lineales c(x) o a las igualdades ceq(x) definidas en nonlcon. La función optimiza de tal manera que c(x) ≤ 0 y ceq(x) = 0. Si no existen límites, establezca lb = [] o ub = [], o ambas.

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) resuelve el problema minimax con las opciones de optimización especificadas en options. Utilice optimoptions para configurar estas opciones.

x = fminimax(problem) resuelve el problema minimax para problem, una estructura descrita en problem.

[x,fval] = fminimax(___), para cualquier sintaxis, devuelve los valores de las funciones objetivo calculadas en fun en la solución x.

[x,fval,maxfval,exitflag,output] = fminimax(___) devuelve además el valor máximo de las funciones objetivo en la solución x, un valor exitflag que describe la condición de salida de fminimax y una estructura output con información sobre el proceso de optimización.

[x,fval,maxfval,exitflag,output,lambda] = fminimax(___) devuelve adicionalmente una estructura lambda cuyos campos contienen los multiplicadores de Lagrange en la solución x.

Ejemplos

Minimizar el máximo de sin y cos

Cree una gráfica de las funciones sin y cos y su máximo sobre el intervalo [–pi,pi].

t = linspace(-pi,pi);
plot(t,sin(t),'r-')
hold on
plot(t,cos(t),'b-');
plot(t,max(sin(t),cos(t)),'ko')
legend('sin(t)','cos(t)','max(sin(t),cos(t))','Location','NorthWest')

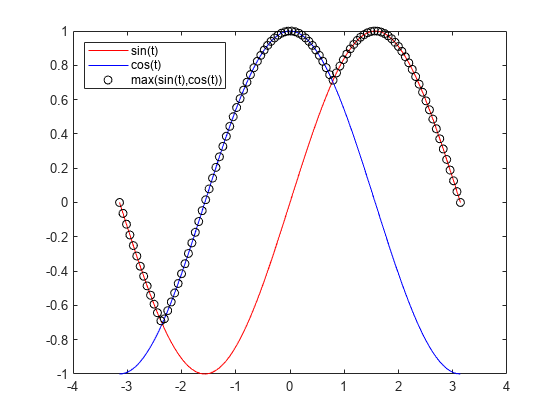
La gráfica muestra dos mínimos locales del máximo, uno cerca de 1 y el otro cerca de -2. Encuentre el mínimo cercano a 1.

fun = @(x)[sin(x);cos(x)];
x0 = 1;
x1 = fminimax(fun,x0)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

x1 = 0.7854

Encuentre el mínimo cercano a -2.

x0 = -2;
x2 = fminimax(fun,x0)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

x2 = -2.3562

Resolver un problema minimax con restricciones lineales

Las funciones objetivo de este ejemplo son lineales con constantes. Para ver una descripción y una gráfica de las funciones objetivo, consulte Comparar fminimax y fminunc.

Establezca las funciones objetivo como tres funciones lineales con el formato $$dot(x,v)+v_0$$ para tres vectores $$v$$ y tres constantes $$v_0$$.

a = [1;1];
b = [-1;1];
c = [0;-1];
a0 = 2;
b0 = -3;
c0 = 4;
fun = @(x)[x*a+a0,x*b+b0,x*c+c0];

Encuentre el punto minimax sujeto a la desigualdad x(1) + 3*x(2) <= –4.

A = [1,3];
b = -4;
x0 = [-1,-2];
x = fminimax(fun,x0,A,b)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

x = 1×2

   -5.8000    0.6000

Resolver un problema minimax con límites y restricciones

Las funciones objetivo de este ejemplo son lineales con constantes. Para ver una descripción y una gráfica de las funciones objetivo, consulte Comparar fminimax y fminunc.

Establezca las funciones objetivo como tres funciones lineales con el formato $$dot(x,v)+v_0$$ para tres vectores $$v$$ y tres constantes $$v_0$$.

a = [1;1];
b = [-1;1];
c = [0;-1];
a0 = 2;
b0 = -3;
c0 = 4;
fun = @(x)[x*a+a0,x*b+b0,x*c+c0];

Establezca límites en los que –2 <= x(1) <= 2 y –1 <= x(2) <= 1, y resuelva el problema minimax partiendo de [0,0].

lb = [-2,-1];
ub = [2,1];
x0 = [0,0];
A = []; % No linear constraints
b = [];
Aeq = [];
beq = [];
[x,fval] = fminimax(fun,x0,A,b,Aeq,beq,lb,ub)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

x = 1×2

   -0.0000    1.0000

fval = 1×3

    3.0000   -2.0000    3.0000

En este caso, la solución no es única. Muchos puntos satisfacen las restricciones y tienen el mismo valor minimax. Represente la superficie con el máximo de las tres funciones objetivo y represente con una línea roja los puntos que tienen el mismo valor minimax.

[X,Y] = meshgrid(linspace(-2,2),linspace(-1,1));
Z = max(fun([X(:),Y(:)]),[],2);
Z = reshape(Z,size(X));
surf(X,Y,Z,'LineStyle','none')
view(-118,28)
hold on
line([-2,0],[1,1],[3,3],'Color','r','LineWidth',8)
hold off

Encontrar el minimax sujeto a restricciones no lineales

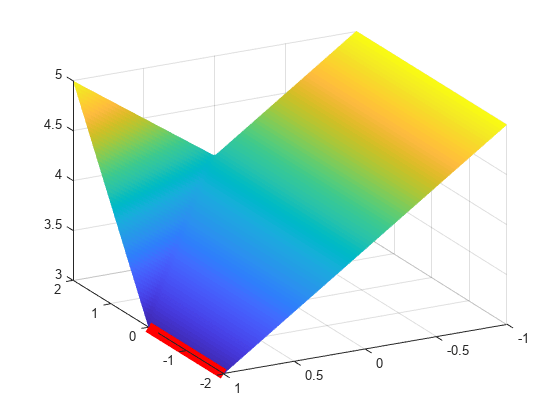
Las funciones objetivo de este ejemplo son lineales con constantes. Para ver una descripción y una gráfica de las funciones objetivo, consulte Comparar fminimax y fminunc.

Establezca las funciones objetivo como tres funciones lineales con el formato $$dot(x,v)+v_0$$ para tres vectores $$v$$ y tres constantes $$v_0$$.

a = [1;1];
b = [-1;1];
c = [0;-1];
a0 = 2;
b0 = -3;
c0 = 4;
fun = @(x)[x*a+a0,x*b+b0,x*c+c0];

La función unitdisk representa la restricción de desigualdad no lineal $$\Vert x{\Vert }^2\le 1$$.

type unitdisk

function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [];

Resuelva el problema minimax sujeto a la restricción unitdisk, partiendo de x0 = [0,0].

x0 = [0,0];
A = []; % No other constraints
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = @unitdisk;
x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

x = 1×2

   -0.0000    1.0000

Resolver un problema minimax utilizando el valor absoluto de un objetivo

fminimax puede minimizar el máximo de $$F_i(x)$$ o $$|F_i(x)|$$ para los primeros valores de $$i$$ utilizando la opción AbsoluteMaxObjectiveCount. Para minimizar los valores absolutos de $$k$$ de los objetivos, ordene los valores de la función objetivo de modo que los valores de $$F_1(x)$$ a $$F_k(x)$$ sean los objetivos para la minimización absoluta, y establezca la opción AbsoluteMaxObjectiveCount en k.

En este ejemplo, minimice el máximo de sin y cos, especifique sin como primer objetivo y establezca AbsoluteMaxObjectiveCount en 1.

fun = @(x)[sin(x),cos(x)];
options = optimoptions('fminimax','AbsoluteMaxObjectiveCount',1);
x0 = 1;
A = []; % No constraints
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
x1 = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

x1 = 0.7854

Intente empezar desde x0 = –2.

x0 = -2;
x2 = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

x2 = -3.1416

Represente la función.

t = linspace(-pi,pi);
plot(t,max(abs(sin(t)),cos(t)))

Para ver el efecto de la opción AbsoluteMaxObjectiveCount, compare esta gráfica con la del ejemplo Minimizar el máximo de sin y cos.

Obtener el valor minimax

Obtenga tanto la ubicación del punto minimax como el valor de las funciones objetivo. Para ver una descripción y una gráfica de las funciones objetivo, consulte Comparar fminimax y fminunc.

Establezca las funciones objetivo como tres funciones lineales con el formato $$dot(x,v)+v_0$$ para tres vectores $$v$$ y tres constantes $$v_0$$.

a = [1;1];
b = [-1;1];
c = [0;-1];
a0 = 2;
b0 = -3;
c0 = 4;
fun = @(x)[x*a+a0,x*b+b0,x*c+c0];

Establezca el punto inicial en [0,0] y encuentre el punto y el valor minimax.

x0 = [0,0];
[x,fval] = fminimax(fun,x0)

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

x = 1×2

   -2.5000    2.2500

fval = 1×3

    1.7500    1.7500    1.7500

Las tres funciones objetivo tienen el mismo valor en el punto minimax. Los problemas sin restricciones suelen tener al menos dos objetivos iguales en la solución, porque si un punto no es un mínimo local de ningún objetivo y solo un objetivo tiene el valor máximo, el objetivo máximo puede reducirse.

Obtener todas las salidas minimax

Las funciones objetivo de este ejemplo son lineales con constantes. Para ver una descripción y una gráfica de las funciones objetivo, consulte Comparar fminimax y fminunc.

Establezca las funciones objetivo como tres funciones lineales con el formato $$dot(x,v)+v_0$$ para tres vectores $$v$$ y tres constantes $$v_0$$.

a = [1;1];
b = [-1;1];
c = [0;-1];
a0 = 2;
b0 = -3;
c0 = 4;
fun = @(x)[x*a+a0,x*b+b0,x*c+c0];

Encuentre el punto minimax sujeto a la desigualdad x(1) + 3*x(2) <= –4.

A = [1,3];
b = -4;
x0 = [-1,-2];

Establezca las opciones para obtener la visualización iterativa y obtenga todas las salidas del solver.

options = optimoptions('fminimax','Display','iter');
Aeq = []; % No other constraints
beq = [];
lb = [];
ub = [];
nonlcon = [];
[x,fval,maxfval,exitflag,output,lambda] =...
    fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

                  Objective        Max     Line search     Directional 
 Iter F-count         value    constraint   steplength      derivative   Procedure 
    0      4              0             6                                            
    1      9              5             0            1           0.981     
    2     14          4.889             0            1          -0.302    Hessian modified twice  
    3     19            3.4     8.132e-09            1          -0.302    Hessian modified twice  

Local minimum possible. Constraints satisfied.

fminimax stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are 
satisfied to within the value of the constraint tolerance.

x = 1×2

   -5.8000    0.6000

fval = 1×3

   -3.2000    3.4000    3.4000

maxfval = 3.4000

exitflag = 4

output = struct with fields:
         iterations: 4
          funcCount: 19
       lssteplength: 1
           stepsize: 6.0684e-10
          algorithm: 'active-set'
      firstorderopt: []
    constrviolation: 8.1323e-09
            message: 'Local minimum possible. Constraints satisfied....'

lambda = struct with fields:
         lower: [2x1 double]
         upper: [2x1 double]
         eqlin: [0x1 double]
      eqnonlin: [0x1 double]
       ineqlin: 0.2000
    ineqnonlin: [0x1 double]

Analice la información devuelta:

• Dos valores de la función objetivo son iguales en la solución.

• El solver converge en 4 iteraciones y 19 evaluaciones de función.

• El valor lambda.ineqlin es distinto de cero, lo que indica que la restricción lineal está activa en la solución.

Argumentos de entrada

fun — Funciones objetivo

identificador de función | nombre de función

Funciones objetivo, especificadas como un identificador de función o un nombre de función. fun es una función que acepta un vector x y devuelve un vector F, con las funciones objetivo evaluadas en x. Puede especificar la función fun como un identificador de función para un archivo de función:

x = fminimax(@myfun,x0,goal,weight)

donde myfun es una función de MATLAB^® como

function F = myfun(x)
F = ...         % Compute function values at x.

fun también puede ser un identificador de función para una función anónima.

x = fminimax(@(x)sin(x.*x),x0,goal,weight);

fminimax pasa x a la función objetivo y a todas las funciones de restricción no lineales en forma de argumento x0. Por ejemplo, si x0 es un arreglo de 5 por 3, fminimax pasa x a fun como un arreglo de 5 por 3. Sin embargo, fminimax multiplica las matrices de restricción lineales A o Aeq por x después de convertir x en el vector columna x(:).

Para minimizar los valores absolutos en el peor de los casos de algunos elementos del vector F(x) (es decir, min{max abs{F(x)} } ), realice la partición de esos objetivos en los primeros elementos de F y utilice optimoptions para establecer la opción AbsoluteMaxObjectiveCount en el número de estos objetivos. Deben realizarse particiones en estos objetivos en los primeros elementos del vector F devuelto por fun. Para ver un ejemplo, consulte Resolver un problema minimax utilizando el valor absoluto de un objetivo.

Suponga que los gradientes de las funciones objetivo también se pueden calcular y la opción SpecifyObjectiveGradient es true, tal y como se establece en:

options = optimoptions('fminimax','SpecifyObjectiveGradient',true)

En este caso, la función fun debe devolver, en el segundo argumento de salida, los valores del gradiente G (una matriz) en x. El gradiente consiste en la derivada parcial dF/dx de cada F en el punto x. Si F es un vector de longitud m y x tiene una longitud n, donde n es la longitud de x0, entonces el gradiente G de F(x) es una matriz de n por m donde G(i,j) es la derivada parcial de F(j) con respecto a x(i) (es decir, la j-ésima columna de G es el gradiente de la j-ésima función objetivo F(j)). Si define F como un arreglo, la discusión anterior se aplica a F(:), el ordenamiento lineal del arreglo F. En cualquier caso, G es una matriz en 2D.

Nota

Establecer SpecifyObjectiveGradient en true solo es efectivo cuando el problema no tiene una restricción no lineal o cuando el problema tiene una restricción no lineal con SpecifyConstraintGradient establecido en true. Internamente, el objetivo se pliega en las restricciones, por lo que el solver necesita ambos gradientes (objetivo y restricción) suministrados con el fin de evitar estimar un gradiente.

Tipos de datos: char | string | function_handle

x0 — Punto inicial

vector real | arreglo real

Punto inicial, especificado como un vector real o un arreglo real. Los solvers utilizan el número de elementos en x0 y el tamaño de x0 para determinar el número y el tamaño de las variables que fun acepta.

Ejemplo: x0 = [1,2,3,4]

Tipos de datos: double

A — Restricciones de desigualdad lineales

matriz real

Restricciones de desigualdad lineales, especificadas como una matriz real. A es una matriz de M por N, donde M es el número de desigualdades y N es el número de variables (número de elementos de x0). Para problemas grandes, pase A como una matriz dispersa.

A codifica las M desigualdades lineales

A*x <= b,

donde x es el vector columna de N variables x(:) y b es un vector columna con M elementos.

Por ejemplo, considere estas desigualdades:

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30,

Especifique las desigualdades introduciendo las siguientes restricciones.

A = [1,2;3,4;5,6];
b = [10;20;30];

Ejemplo: Para especificar que los componentes de x suman 1 o menos, utilice A = ones(1,N) y b = 1.

Tipos de datos: double

b — Restricciones de desigualdad lineales

vector real

Restricciones de desigualdad lineales, especificadas como un vector real. b es un vector de M elementos relacionado con la matriz A. Si pasa b como un vector fila, los solvers convierten internamente b en el vector columna b(:). Para problemas grandes, pase b como un vector disperso.

b codifica las M desigualdades lineales

A*x <= b,

donde x es el vector columna de N variables x(:) y A es una matriz de tamaño M por N.

Por ejemplo, considere estas desigualdades:

x₁ + 2x₂ ≤ 10
3x₁ + 4x₂ ≤ 20
5x₁ + 6x₂ ≤ 30.

Especifique las desigualdades introduciendo las siguientes restricciones.

A = [1,2;3,4;5,6];
b = [10;20;30];

Ejemplo: Para especificar que los componentes de x suman 1 o menos, utilice A = ones(1,N) y b = 1.

Tipos de datos: double

Aeq — Restricciones de igualdad lineales

matriz real

Restricciones de igualdad lineales, especificadas como una matriz real. Aeq es una matriz de Me por N, donde Me es el número de igualdades y N es el número de variables (número de elementos de x0). Para problemas grandes, pase Aeq como una matriz dispersa.

Aeq codifica las Me igualdades lineales

Aeq*x = beq,

donde x es el vector columna de N variables x(:) y beq es un vector columna con Me elementos.

Por ejemplo, considere estas desigualdades:

x₁ + 2x₂ + 3x₃ = 10
2x₁ + 4x₂ + x₃ = 20,

Especifique las desigualdades introduciendo las siguientes restricciones.

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Ejemplo: Para especificar que los componentes de x suman 1, utilice Aeq = ones(1,N) y beq = 1.

Tipos de datos: double

beq — Restricciones de igualdad lineales

vector real

Restricciones de igualdad lineales, especificadas como un vector real. beq es un vector de Me elementos relacionado con la matriz Aeq. Si pasa beq como un vector fila, los solvers convierten internamente beq en el vector columna beq(:). Para problemas grandes, pase beq como un vector disperso.

beq codifica las Me igualdades lineales

Aeq*x = beq,

donde x es el vector columna de N variables x(:) y Aeq es una matriz de tamaño Me por N.

Por ejemplo, considere estas igualdades:

x₁ + 2x₂ + 3x₃ = 10
2x₁ + 4x₂ + x₃ = 20.

Especifique las igualdades introduciendo las siguientes restricciones.

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Ejemplo: Para especificar que los componentes de x suman 1, utilice Aeq = ones(1,N) y beq = 1.

Tipos de datos: double

lb — Límites inferiores

vector real | arreglo real

Límites inferiores, especificados como un vector real o un arreglo real. Si el número de elementos en x0 es igual al número de elementos en lb, entonces lb especifica que

x(i) >= lb(i) para todo i.

Si numel(lb) < numel(x0), entonces lb especifica que

x(i) >= lb(i) para 1 <= i <= numel(lb).

Si lb tiene menos elementos que x0, los solvers emiten una advertencia.

Ejemplo: Para especificar que todos los componentes de x son positivos, utilice lb = zeros(size(x0)).

Tipos de datos: double

ub — Límites superiores

vector real | arreglo real

Límites superiores, especificados como un vector real o un arreglo real. Si el número de elementos en x0 es igual al número de elementos en ub, entonces ub especifica que

x(i) <= ub(i) para todo i.

Si numel(ub) < numel(x0), entonces ub especifica que

x(i) <= ub(i) para 1 <= i <= numel(ub).

Si ub tiene menos elementos que x0, los solvers emiten una advertencia.

Ejemplo: Para especificar que todos los componentes de x son menores que 1, utilice ub = ones(size(x0)).

Tipos de datos: double

nonlcon — Restricciones no lineales

identificador de función | nombre de función

Límites no lineales, especificados como un identificador de función o un nombre de función. nonlcon es una función que acepta un vector o arreglo x y devuelve dos arreglos, c(x) y ceq(x).

• c(x) es el arreglo de restricciones de desigualdad no lineales de x. fminimax intenta satisfacer

  c(x) <= 0 for all entries of c.

• ceq(x) es el arreglo de restricciones de igualdad no lineales de x. fminimax intenta satisfacer

  ceq(x) = 0 for all entries of ceq.

Por ejemplo:

x = fminimax(@myfun,x0,...,@mycon)

donde mycon es una función de MATLAB como la siguiente:

function [c,ceq] = mycon(x)
c = ...     % Compute nonlinear inequalities at x.
ceq = ...   % Compute nonlinear equalities at x.

Suponga que los gradientes de las restricciones también pueden calcularse y la opción SpecifyConstraintGradient es true, según establece:

options = optimoptions('fminimax','SpecifyConstraintGradient',true)

En este caso, la función nonlcon también debe devolver, en el tercer y el cuarto argumentos de salida, GC, el gradiente de c(x) y GCeq, el gradiente de ceq(x). Consulte Restricciones no lineales para obtener una explicación de cómo "condicionar" los gradientes para usarlos en solvers que no aceptan gradientes suministrados.

Si nonlcon devuelve un vector c de m componentes y x tiene longitud n, donde n es la longitud de x0, el gradiente GC de c(x) es una matriz de n por m, donde GC(i,j) es la derivada parcial de c(j) con respecto a x(i) (es decir, la j-ésima columna de GC es el gradiente de la j-ésima restricción de desigualdad c(j)). Del mismo modo, si ceq tiene p componentes, el gradiente GCeq de ceq(x) es una matriz de n por p, donde GCeq(i,j) es la derivada parcial de ceq(j) con respecto a x(i) (es decir, la j-ésima columna de GCeq es el gradiente de la j-ésima restricción de igualdad ceq(j)).

Nota

Configurar SpecifyConstraintGradient como true solo es efectivo cuando SpecifyObjectiveGradient se establece en true. Internamente, el objetivo se pliega en la restricción, por lo que el solver necesita ambos gradientes (objetivo y restricción) suministrados con el fin de evitar estimar un gradiente.

Nota

Dado que las funciones de Optimization Toolbox™ solo aceptan entradas de tipo double, las funciones objetivo y de restricción no lineal suministradas por el usuario deben devolver salidas de tipo double.

Consulte Pasar parámetros adicionales para obtener una explicación de cómo parametrizar la función de restricción no lineal nonlcon, si es necesario.

Tipos de datos: char | function_handle | string

options — Opciones de optimización

salida de optimoptions | estructura como la que devuelve optimset

Opciones de optimización, especificadas como la salida de optimoptions o una estructura como la que devuelve optimset.

Algunas opciones no aparecen en la visualización optimoptions. Estas opciones se muestran en cursiva en la siguiente tabla. Para obtener más detalles, consulte Consultar las opciones de optimización.

Para obtener más información sobre las opciones que tienen nombres distintos para optimset, consulte Nombres de opciones actuales y antiguos.

Opción	Descripción
AbsoluteMaxObjectiveCount	Número de elementos de Fi(x) para los que desea minimizar el valor absoluto de Fi. Consulte Resolver un problema minimax utilizando el valor absoluto de un objetivo. Para optimset, el nombre es MinAbsMax.
ConstraintTolerance	Tolerancia de terminación en la vulneración de restricciones (un escalar positivo). La opción predeterminada es 1e-6. Consulte Tolerancias y criterios de detención. Para optimset, el nombre es TolCon.
Diagnóstico	Visualización de información de diagnóstico sobre la función que se desea minimizar o resolver. Las opciones son 'on' u 'off' (que es la opción predeterminada).
DiffMaxChange	Cambio máximo en variables para gradientes de diferencias finitas (un escalar positivo). La opción predeterminada es Inf.
DiffMinChange	Cambio mínimo en variables para gradientes de diferencias finitas (un escalar positivo). La opción predeterminada es 0.
Display	Nivel de visualización (consulte Visualización iterativa): 'off' o 'none' no muestran salida alguna. 'iter' muestra la salida en cada iteración y emite el mensaje de salida predeterminado. 'iter-detailed' muestra la salida en cada iteración y emite el mensaje de salida técnico. 'notify' solo muestra la salida si la función no converge y emite el mensaje de salida predeterminado. 'notify-detailed' solo muestra la salida si la función no converge y emite el mensaje de salida técnico. 'final' (predeterminada) solo muestra la salida final y emite el mensaje de salida predeterminado. 'final-detailed' solo muestra la salida final y emite el mensaje de salida técnico.
FiniteDifferenceStepSize	Factor de tamaño de paso de escalar o vector para diferencias finitas. Cuando establece FiniteDifferenceStepSize en un vector v, las diferencias finitas progresivas delta son delta = v.*sign′(x).*max(abs(x),TypicalX); , donde sign′(x) = sign(x) excepto sign′(0) = 1. Las diferencias finitas centrales son delta = v.*max(abs(x),TypicalX); Un escalar FiniteDifferenceStepSize se expande a un vector. La opción predeterminada es sqrt(eps) para diferencias finitas progresivas y eps^(1/3) para diferencias finitas centrales. Para optimset, el nombre es FinDiffRelStep.
FiniteDifferenceType	Tipo de diferencias finitas utilizadas para estimar gradientes, ya sea 'forward' (valor predeterminado) o 'central' (centradas). La opción 'central' requiere el doble de evaluaciones de función, pero suele ser más precisa. El algoritmo respeta escrupulosamente los límites cuando estima ambos tipos de diferencias finitas. Por ejemplo, podría seleccionar una diferencia regresiva en lugar de progresiva para evitar realizar la evaluación en un punto fuera de los límites. Para optimset, el nombre es FinDiffType.
FunctionTolerance	Tolerancia de terminación en el valor de la función (un escalar positivo). La opción predeterminada es 1e-6. Consulte Tolerancias y criterios de detención. Para optimset, el nombre es TolFun.
FunValCheck	Comprobación que indica si los valores de la función objetivo y de las restricciones son válidos. 'on' muestra un error cuando la función objetivo o las restricciones devuelven un valor complex, Inf o NaN. La opción predeterminada 'off' no muestra ningún error.
MaxFunctionEvaluations	Número máximo de evaluaciones de función permitidas (un entero positivo). La opción predeterminada es 100*numberOfVariables. Consulte Tolerancias y criterios de detención y Iteraciones y recuentos de la función. Para optimset, el nombre es MaxFunEvals.
MaxIterations	Número máximo de iteraciones permitidas (un entero positivo). La opción predeterminada es 400. Consulte Tolerancias y criterios de detención y Iteraciones y recuentos de la función. Para optimset, el nombre es MaxIter.
MaxSQPIter	Número máximo de iteraciones SQP permitidas (un entero positivo). La opción predeterminada es 10*max(numberOfVariables, numberOfInequalities + numberOfBounds).
MeritFunction	Si esta opción se establece en 'multiobj' (el valor predeterminado), use la consecución de metas o la función de mérito minimax. Si esta opción se establece en 'singleobj' use la función de mérito fmincon.
OptimalityTolerance	Tolerancia de terminación en la optimalidad de primer orden (un escalar positivo). La opción predeterminada es 1e-6. Consulte Medida de optimalidad de primer orden. Para optimset, el nombre es TolFun.
OutputFcn	Una o varias funciones definidas por el usuario a las que una función de optimización llame en cada iteración. Pase un identificador de función o un arreglo de celdas de identificadores de función. La opción predeterminada es ninguno ([]). Consulte Sintaxis de función de salida y función de gráfica.
PlotFcn	Gráficas que muestran varias medidas de progreso mientras se ejecuta el algoritmo. Seleccione una de las gráficas predefinidas o escriba la suya propia. Pase un nombre, identificador de función o arreglo de celdas de nombres o identificadores de función. Para funciones de gráfica personalizadas, pase identificadores de función. La opción predeterminada es ninguno ([]). 'optimplotx' representa el punto actual. 'optimplotfunccount' representa el recuento de la función. 'optimplotfval' representa los valores de la función objetivo. 'optimplotconstrviolation' representa la vulneración de restricciones máxima. 'optimplotstepsize' representa el tamaño de paso. Las funciones de gráfica personalizadas utilizan la misma sintaxis que las funciones de salida. Consulte Funciones de salida para Optimization Toolbox y Sintaxis de función de salida y función de gráfica. Para optimset, el nombre es PlotFcns.
RelLineSrchBnd	Límite relativo (un valor de escalar no negativo real) de la longitud de paso de búsqueda de recta, tal que el desplazamiento total en x satisface |Δx(i)| ≤ relLineSrchBnd· max(|x(i)|,|typicalx(i)|). Esta opción permite controlar la magnitud de los desplazamientos de x cuando el solver dé pasos demasiado grandes. La opción predeterminada es ninguno ([]).
RelLineSrchBndDuration	Número de iteraciones para el cual debe estar activo el límite que se especifica en RelLineSrchBnd. La opción predeterminada es 1.
SpecifyConstraintGradient	Gradiente para las funciones de restricción no lineales definidas por el usuario. Cuando esta opción se establece en true, fminimax espera que la función de restricción tenga cuatro salidas, según se describe en nonlcon. Cuando esta opción se establece en false (el valor predeterminado), fminimax estima los gradientes de las restricciones no lineales mediante diferencias finitas. Para optimset, el nombre es GradConstr y los valores son 'on' u 'off'.
SpecifyObjectiveGradient	Gradiente para la función objetivo definida por el usuario. Consulte la descripción de fun para ver cómo definir el gradiente. Establezca esta opción en true para hacer que fminimax utilice un gradiente definido por el usuario de la función objetivo. La opción predeterminada, false, hace que fminimax estime los gradientes utilizando diferencias finitas. Para optimset, el nombre es GradObj y los valores son 'on' u 'off'.
StepTolerance	Tolerancia de terminación en x (un escalar positivo). El valor predeterminado es 1e-6. Consulte Tolerancias y criterios de detención. Para optimset, el nombre es TolX.
TolConSQP	Tolerancia de terminación en la vulneración de restricciones SQP de iteración interior (un escalar positivo). La opción predeterminada es 1e-6.
TypicalX	Valores x típicos. El número de elementos en TypicalX es igual al número de elementos en x0, el punto de inicio. El valor predeterminado es ones(numberofvariables,1). La función fminimax utiliza TypicalX para escalar las diferencias finitas para la estimación de gradientes.
UseParallel	Opción para utilizar la computación paralela. Cuando esta opción se establece en true, fminimax estima los gradientes en paralelo. La opción predeterminada es false. Consulte Computación paralela.

Ejemplo: optimoptions('fminimax','PlotFcn','optimplotfval')

problem — Estructura de problema

estructura

Estructura de problema, especificada como una estructura con los campos de esta tabla.

Nombre de campo	Entrada
objective	Función objetivo fun
x0	Punto inicial para x
Aineq	Matriz para restricciones de desigualdad lineales
bineq	Vector para restricciones de desigualdad lineales
Aeq	Matriz para restricciones de igualdad lineales
beq	Vector para restricciones de igualdad lineales
lb	Vector de límites inferiores
ub	Vector de límites superiores
nonlcon	Función de restricción no lineal
solver	'fminimax'
options	Opciones creadas con optimoptions

Debe proporcionar al menos los campos objective, x0, solver y options en la estructura problem.

Tipos de datos: struct

Argumentos de salida

x — Solución

vector real | arreglo real

Solución, devuelta como un vector real o un arreglo real. El tamaño de x es el mismo que el tamaño de x0. Habitualmente, x es una solución local al problema cuando exitflag es positivo. Para obtener información sobre la calidad de la solución, consulte Cuando el solver tiene éxito.

fval — Valores de la función objetivo en la solución

arreglo real

Valores de la función objetivo en la solución, devueltos como un arreglo real. Por lo general, fval = fun(x).

maxfval — Máximo de los valores de la función objetivo en la solución

escalar real

Máximo de los valores de la función objetivo en la solución, devuelto como un escalar real. maxfval = max(fval(:)).

exitflag — Razón por la que fminimax se ha detenido

valor entero

Razón por la que fminimax se ha detenido, devuelta como un entero.

1	La función ha convergido a una solución x
4	La magnitud de la dirección de búsqueda fue inferior a la tolerancia especificada y la vulneración de la restricción fue inferior a options.ConstraintTolerance
5	La magnitud de la derivada direccional fue inferior a la tolerancia especificada y la vulneración de la restricción fue inferior a options.ConstraintTolerance
0	El número de iteraciones superó options.MaxIterations o el número de evaluaciones de función superó options.MaxFunctionEvaluations
-1	Detenido por una función de salida o una función de gráfica
-2	No se ha encontrado ningún punto factible.

output — Información sobre el proceso de optimización

estructura

Información sobre el proceso de optimización, devuelta como estructura con los campos de esta tabla.

iterations	Número de iteraciones realizadas
funcCount	Número de evaluaciones de función
lssteplength	Tamaño del paso de búsqueda de recta relativo a la dirección de búsqueda
constrviolation	Máximo de funciones de restricción
stepsize	Longitud del último desplazamiento en x
algorithm	Algoritmo de optimización utilizado
firstorderopt	Medida de optimalidad de primer orden
message	Mensaje de salida

lambda — Multiplicadores de Lagrange en la solución

estructura

Multiplicadores de Lagrange en la solución, devueltos como una estructura con los campos de esta tabla.

lower	Límites inferiores que corresponden a lb
upper	Límites superiores que corresponden a ub
ineqlin	Desigualdades lineales que corresponden a A y b
eqlin	Igualdades lineales que corresponden a Aeq y beq
ineqnonlin	Desigualdades no lineales que corresponden a c en nonlcon
eqnonlin	Igualdades no lineales que corresponden a ceq en nonlcon

Algoritmos

fminimax resuelve un problema minimax convirtiéndolo en un problema de consecución de metas y resolviendo a continuación el problema de consecución de metas convertido utilizando fgoalattain. La conversión pone todos los objetivos a 0 y todas las ponderaciones a 1. Consulte Ecuación 1 en Multiobjective Optimization Algorithms.

Funcionalidad alternativa

App

La tarea Optimize de Live Editor proporciona una interfaz visual para fminimax.

Capacidades ampliadas

Soporte paralelo automático

Acelere código mediante la ejecución automática de cálculo paralelo mediante Parallel Computing Toolbox™.

Para ejecutar en paralelo, establezca la opción 'UseParallel' en true.

options = optimoptions('solvername','UseParallel',true)

Para obtener más información, consulte Usar la computación paralela en Optimization Toolbox.

Historial de versiones

Introducido antes de R2006a

Consulte también

fgoalattain | optimoptions | Optimize

Temas

• Crear un identificador de función
• Optimización multiobjetivo