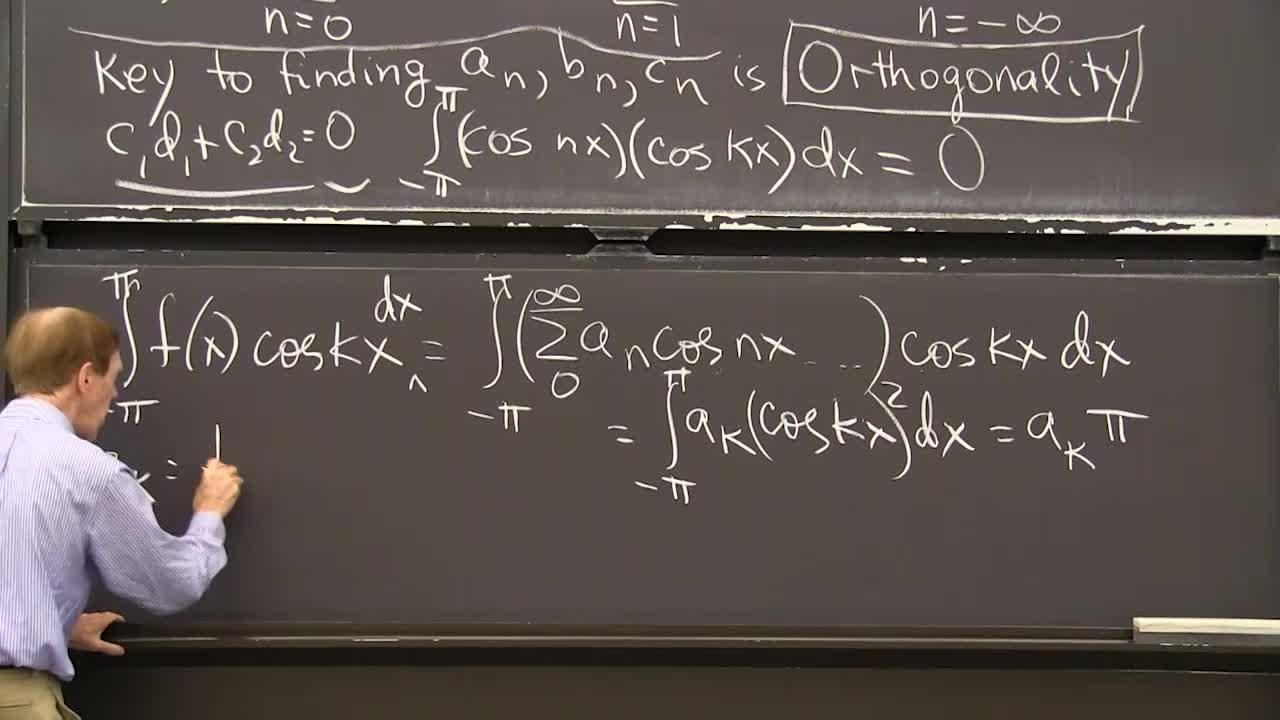Differential Equations and Linear Algebra, 8.1: Fourier Series
From the series: Differential Equations and Linear Algebra
Gilbert Strang, Massachusetts Institute of Technology (MIT)
A Fourier series separates a periodic function F(x) into a combination (infinite) of all basis functions cos(nx) and sin(nx).
Published: 27 Jan 2016
OK, I'm going to explain Fourier series, and that I can't do in 10 minutes. It'll take two, maybe three, sessions to see enough examples to really use the idea. Let me start with what we're looking for. We have a function. And we want to write it as a combination of cosines and sines. So those our basis functions-- the cosines and the sine.
And a n's and the b n's are the coefficients that we have to look for. That tells us how much of cosine nx is in the big function f of x. Notice that the cosines start at n equals 0, because cosine of 0 is 1. So there's an a0 in our sum. But there isn't a b0, because n equals zero of the sine would be zero, and we don't get anything there.
So we're looking for the a n's and b n's. And, really, I want to show you, at the same time, the complex form with coefficient cn. And now n goes from minus infinity to infinity. That's really the more beautiful form because that one formula for cn does the job, whereas here I will need a separate formula for a n and for bn.
OK. So this is natural when the function is real, but in the end, and for the discrete Fourier transform, and for the fast Fourier transform, the complex case will win. And, of course, everybody sees that e to the inx, by Euler's great formula, is a combination of cosine nx and sine nx. So, I can use those, or I can use cosine and sine.
OK. So, how do you find these numbers? The key is orthogonality. So that's the first central idea here in Fourier series, is the idea of orthogonality. Now what does that mean? That means perpendicular. And for a vector, and a second vector, we have an idea of what perpendicular means. The 90 degree angle between them. And we check that by the dot product-- or inner product, whichever name you like-- between the two vectors should be 0.
OK. But here we have functions-- like cosine functions. So here's one cosine, and here's a different cosine. So those are two different basis functions-- say, cosine of 7x and cosine of 12 x. The coefficients a7 and a12 would tell us how much of cosine 7x is in the function.
You see, we're separating the function into frequencies. We're looking into pure oscillations, pure harmonics. And we expect, probably, that's the lower harmonics the smoother ones cos x, cos 2x, cos 3x, have most of the energy. And the high harmonics, cosine 12x, cosine 100x, probably those are quickly alternating, those contain noise, and high frequency. Quick changes in the function will show up in the high frequencies.
OK. So what's the answer to this integral-- cosine of 7x times cosine of 12x dx, over the range minus pi to pi? Orthogonality comes in, the answer is 0. That's the crucial fact. That's what makes it possible to separate out a7 and a12 and get hold of them. So let me show you how to do that.
So I'm going to use this fact, which is the function version of 90 degree angle. So, you see, it's a little like a dot product. Well, let me remember, a dot product would be something like c1 d1 plus c2 d2 equals 0, if I had a vector c1 c2 and a vector d1 d2. That would be the dot product, and it would be 0 if the vectors are orthogonal. Here, instead of adding, I'm integrating because I have functions. So just that's the meaning of dot product-- the integral of one function times the other function gives 0.
OK. I'll use that now. OK, how will I use this? I will look what I want. This is my goal. I'll multiply both sides of this equation by cosine kx. And then I'll integrate. And the beauty is, that when I multiply by cosine kx, and I integrate, everything goes to zero except what I want. By the way, all the sines times cosine kx integrate to 0. All the sines are orthogonal to all the cosines. And all the cosines will be orthogonal to all the other cosines. So let me show you what I get.
So I multiply my f of x by cosine kx, and I integrate from minus pi to pi. OK? Now, on the right-hand side, this is my integral from minus pi to pi, of my big sum of all these terms, 0 to infinity, a n cos nx, etcetera-- including the sines but I'm not even put them in because they're going to get killed by this integration-- times cosine kx dx. All I did was take the f of x equal that formula, multiplied both sides by cosine kx, and integrated.
And, now the orthogonality pays off, because this times this, when I integrate gives 0, with one exception. When n equals k, then I do get the integral. The only term I get is ak, cosine kx, twice dx. Only k equal n survives this process. And then that integral of cosine squared happens to be pi, so this is just ak times pi. Look, I've discovered what ak is. I've discovered the k Fourier cosine coefficient. I just divide by pi.
So can I just divide by pi to get this formula for ak? Ak is 1 over pi. The integral from minus pi to pi of my function, times cosine kx dx. That's the formula. That tells me the coefficient. And I could only do that with orthogonality to knock out all but one term. And now, if I wanted the sine coefficients, bk, it would be the same formula except that would be a sine.
And if I wanted the complex coefficient, ck, it turns out it'd be the same formula expect-- well maybe it's 2 pi there, 1 over 2 pi-- and this becomes an e to the minus ikx. In a complex case, the complex conjugate e to the minus ikx shows up. So this is really the dot product, the inner product, of the function with the cosine.
OK. So let me do some examples. Maybe I should write up the sine formula that I just mentioned. So bk is the integral 1 over pi, the integral of my function, times sine kx dx. And there's one exception. A0 has a little bit different formula, the pi changes to 2 pi. I'm sorry about that. When k is 0 or it's the integral of 1, from minus pi to pi, and I get 2 pi. So, a0 is 1 over 2 pi-- the integral of f of x times when k is zero cosine-- this is 1 dx. That has a simple meaning. That's the average of f of x.
OK. So the basis function was just 1 when k was zero. When k is 0, the function of my cosine is just one, and I get the integral of the function times 1 divided by 2 pi.
Could we just do an example? So I want to take a function. And in this video why don't I take an easy, but very important, function-- the delta function. So I plan to use these formulas on the delta function.
Let me draw a little picture of the delta function. I'm only going between minus pi and pi, and the delta function, as we know, is 0, it's infinite, at the spike, and 0 again. The reason I wanted to draw it is, that's an even function. That's a function which is symmetric between x and minus x.
And in that case, there will be no sines. Sine functions are odd. The integral from minus pi to pi of an odd function gives 0. The odd means that when you cross x equals 0 you get minus the result for x greater than 0. So my point is, this is an even function-- delta of x is the same as delta of minus x, and only cosines. Good. The sine coefficients automatically dropped our 0 so, of course, the integral would show it. But we see it even before we integrate.
OK I'm ready for the delta function. So I'm going to write delta of x, and we remember what the delta function is-- a combination of cosines. OK. That's the delta function between minus pi and pi. OK. And what's our formula for the a n? Well, you remember we had a special formula for a0, which was 1/2 pi times the integral, from minus pi to pi, of our function, which is delta, times the basis function, which n equals 0, the basis function is 1 dx.
OK, we know the answer to that. We can integrate the delta function. The one key thing about the integral of the delta function is, it's always 1-- if we cross x equals 0, which we will. So that integral is 1 so I'm getting 1/2 pi.
What about the other for a coefficient? So that's 1/pi, now. The integral from minus pi to pi of all of my function times cosine kxdx. You know what I'm doing. I'm using my formula to find the coefficients. My formula says take the function, whatever it is-- and in this example, it's the delta function-- multiply by the cosine, integrate, and divide by the factor pi.
OK. Well, of course, we can do that integral. Because when you integrate a delta function, times some other function, all the action is at x equals 0. At x equals 0, this function is 1. And I don't care what it is elsewhere, it's just 1. So this is the same as integrating delta of x times 1, which gives us-- well, the interval the delta function 1. So that integral is one, so I'm getting 1/pi. Good.
OK. So now, do you want me to write out the series for the delta function? It looks kind of unusual. This is telling us something quite remarkable. It's telling us that all these coefficients are the same. All the frequencies, all the harmonics, are in the delta function in equal amounts. Usually, we would see a big drop off of the coefficients ak, but for the delta function, which is so singular, all a big spike at one point, there's no drop off and no decay in the coefficients, they just constant.
OK. So I'm saying that the delta function is the constant term, 1/2pi, and then 1/pi times cosine of x, and cosine of 2x, and so on. OK. All frequencies there are the same. And I'll stop with that one example here. So the key points were orthogonality, the formulas for the the coefficients, and this example. Thank you.