The Experiment Using Neural Networks | How to Estimate Battery State of Charge Using Deep Learning, Part 2

One thing a neural network needs is lots and lots of training data. The data is labeled and fed to the network, which in turn, tries to learn the patterns of changing the input variables that lead to a certain outcome. So Phil will describe the experimental setup and procedure for designing and performing the measurements for training and testing the neural network. Phil, over to you.

Thank you, Javier, for that excellent introduction of the topic, and for giving us this opportunity to discuss our research. I will provide an overview of the experimental testing, which was performed for this work. First, I will discuss the cells that were tested. Then, I will explain how the drive cycles are calculated, and describe the test equipment used. Finally, I will show some of the experimental results.

Test results for two 18650 form factor, cylindrical battery cells were used in this work. One was a Panasonic 18650PF, NCA Chemistry cell, and the other was an LG HG2 NMC Chemistry cell. Both cells have similar capacity, around three amp hours, and the LG cell has a slightly lower nominal resistance of 28 milliamps. Two cells with different chemistries are used to demonstrate that the neural network SOC estimation algorithm can perform well for either.

To make the results presented in the paper realistic and meaningful, battery cells were tested at a range of temperatures, with drive cycle power profiles calculated for electric vehicle applications. For the Panasonic cells, prototype Ford F150 electric truck, which was built for another project, was modeled with a 35 kilowatt-hour pack, consisting of 3,360 of the cells. For the LG HG2 cells, a Fiat 500e electric vehicle was modeled with a small 7.3 kilowatt-hour pack, consisting of 672 cells.

The power calculated from the model for each tested drive cycle was then scaled for a single cell, and these power profiles were applied to the cells with the battery cycler. Both of these packs are rather small compared to what would be common for a commercial application, and this is intentional. With a small pack, each cell must provide more power, and this makes the SOC estimation problem more challenging, and therefore gives confidence that the developed methodology has potential to perform even better in a real application.

Battery cells were tested at the University of Wisconsin-Madison, where I did my PhD, and also at McMaster University in Hamilton, Ontario, Canada, where this work was performed. The cells were tested using battery cyclers from Digatron Power Electronics. Importantly, the cyclers are very accurate, with voltage and current air no greater than plus or minus 0.1% of full scale. This ensures the data sets are an accurate set of reference data. The cells are placed in a thermal chamber, and a range of dry cycle and characterization tests are performed at temperatures of -10, 0, 10, and 25 degrees C. The LG HG2 battery considered in this study at -10 degrees C, resistance is more than three times greater than at room temperature, as shown in the figure on the left.

And it is more than six times greater at -20 degrees Celsius. Resistance also becomes a non-linear function of current at low temperatures, as is shown in the figure on the right, with resistance for a 2c current pulse that -20 degrees C, being about 30% less than the 0.25 C current pulse. This non-linear resistance is commonly referred to as the Butler Vomer equation resistance, and is known to be more prevalent at low temperatures, as is seen here. When developing a SOC estimation methodology, it is therefore important to consider its performance at low temperatures, where the non-linear temperature dependent characteristics make it much more difficult for algorithms to observe a SOC.

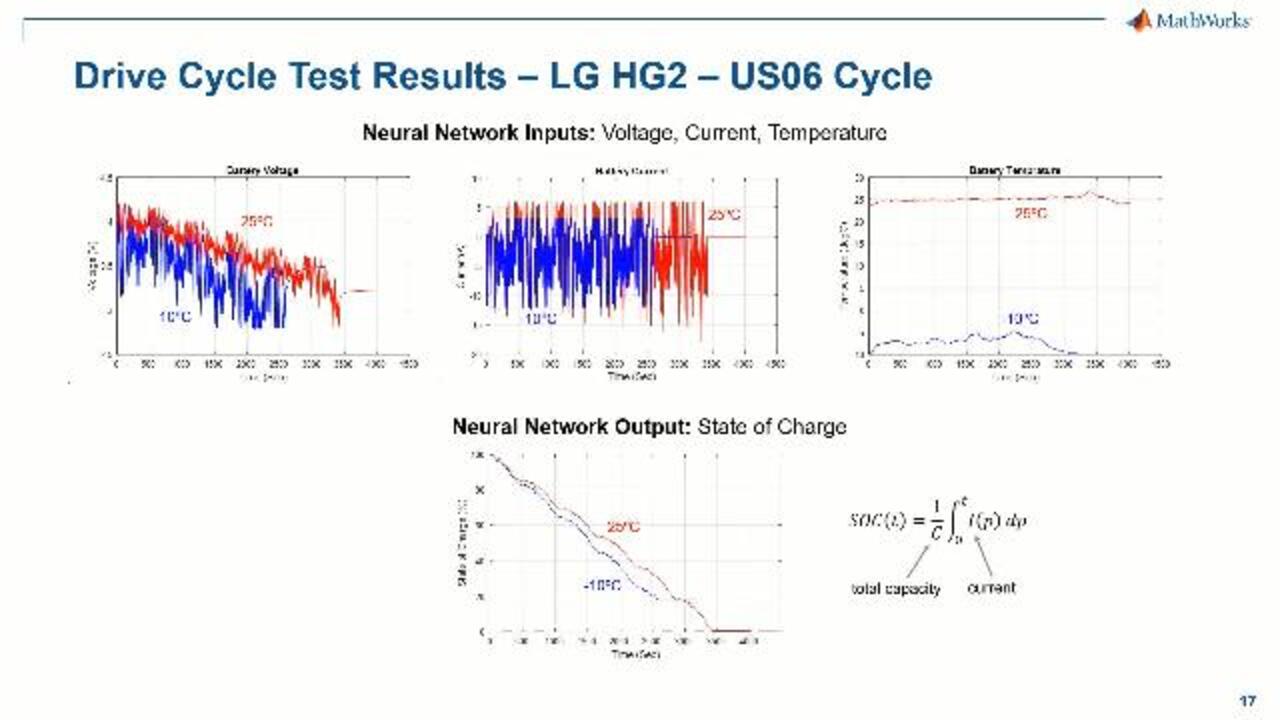
Here are results for one of the tested drive cycles, the aggressive US06 cycle for the LG HG2 cell. The neural network inputs, voltage, current, and temperature, are shown on the top. And the target output value, the state of charge calculated as the integral of the current scale by the capacity, is shown on the bottom. There's quite high voltage deviation, especially at the lower temperature -10 degrees C, with the battery voltage periodically reaching its limit of 0.8 volts, and therefore operating at its maximum power capability. SOC estimation algorithms effectively function as inverse models, which estimate the open circuit voltage, directly or indirectly, and associate the estimated open circuit voltage with state of charge.

Well, for a neural network algorithm, open circuit voltage is not directly estimated with the model, like for the Kalman filter, the learned relationship between SOC and terminal voltage characteristics, still, in theory, rest on the relation between open circuit voltage and SOC, because open circuit voltage is the true electrochemical indicator of state of charge. When there is large voltage deviation from the open circuit voltage, like for the -10 degrees C case, it is much more difficult for these algorithms to accurately and smoothly estimate SOC. And that's why we've chosen such challenging cases to develop and evaluate our algorithms.

It is also important to note that for each drive cycle, the state of charge always starts the same reference 100% state of charge value at the beginning of a drive cycle. This is achieved by always charging the battery at 25 degrees C with the same constant current, constant voltage charging method, even when the drive cycles are performed at lower temperatures, such as 0 degrees C. This aspect of test design ensures that the calculated reference SOC value, which is used for training and evaluating the area of the estimation algorithms, is always as accurate and consistent as possible.

Each battery was tested with many different drive cycles. Portion of these cycles were used for training the SOC estimation algorithm, and the remainder were used for testing the accuracy of the algorithm. For the Panasonic cell, five mixed drive cycles, which are made up of randomized portions of other drive cycles, were used for training and the standard urban UDDS cycle, LA92 cycle, and the more aggressive US06 cycle, were used for testing. For the LG HG2 battery, eight mixed cycles were used for training, and the same cycles were used for testing.

The histograms show that the training and testing cycles covered the whole voltage range of the battery, from around 3 to 4.2 volts, and covered temperatures from -10 to about 30 degrees C, due to the battery warming up during these fixed ambient temperature tests. The training and testing data both cover the operational space well, which is important for thorough training and evaluation of the neural network algorithm. Also, around 2/3 of the data is used for training and 1/3 for testing, the common ratio when utilizing neural networks.

Both of these data sets, which also include temperatures beyond what was used in this study, have been shared online in the Mendeleev Data Repository. Such testing requires a lot of resources, both money and time, so we wanted to share these data sets to make development and testing in battery models om state estimation algorithms more accessible to other researchers and those in industry. We hope to see wider sharing of data sets by others in the future, as well as sharing of the source code for the algorithms, as we have done for the work Carlos will present next.