fit
Ajustar curvas o superficies a datos
Sintaxis
Descripción
fitobject = fit(x,y,fitType,fitOptions)fitOptions.
fitobject = fit(x,y,fitType,Name=Value)fitType con opciones adicionales especificadas por uno o más argumentos de parName=Value. Utilice fitoptions para mostrar nombres de propiedad disponibles y valores predeterminados para el modelo específico de la biblioteca.
Ejemplos
Cargue el conjunto de datos de muestra census.
load census;Los vectores pop y cdate contienen datos sobre el tamaño de la población y el año en que se ha realizado el censo, respectivamente.
Ajuste una curva cuadrática a los datos de población.
f=fit(cdate,pop,'poly2')f =
Linear model Poly2:
f(x) = p1*x^2 + p2*x + p3
Coefficients (with 95% confidence bounds):
p1 = 0.006541 (0.006124, 0.006958)
p2 = -23.51 (-25.09, -21.93)
p3 = 2.113e+04 (1.964e+04, 2.262e+04)
f contiene los resultados del ajuste, incluidas las estimaciones de coeficientes con límites de confianza del 95%.
Represente el ajuste de f junto con una gráfica de dispersión de los datos.
plot(f,cdate,pop)

La gráfica muestra que la curva ajustada sigue de cerca los datos de población.
Cargue el conjunto de datos de muestra franke.
load frankeLos vectores x, y y z contienen datos generados a partir de la función de prueba bivariada de Franke, a la que se añade ruido y escalado.
Ajuste una superficie polinomial a los datos. Especifique un grado de dos para los términos x y un grado de tres para los términos y.
sf = fit([x, y],z,'poly23') Linear model Poly23:
sf(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p21*x^2*y
+ p12*x*y^2 + p03*y^3
Coefficients (with 95% confidence bounds):
p00 = 1.118 (0.9149, 1.321)
p10 = -0.0002941 (-0.000502, -8.623e-05)
p01 = 1.533 (0.7032, 2.364)
p20 = -1.966e-08 (-7.084e-08, 3.152e-08)
p11 = 0.0003427 (-0.0001009, 0.0007863)
p02 = -6.951 (-8.421, -5.481)
p21 = 9.563e-08 (6.276e-09, 1.85e-07)
p12 = -0.0004401 (-0.0007082, -0.0001721)
p03 = 4.999 (4.082, 5.917)
sf contiene los resultados del ajuste, incluidas las estimaciones de coeficientes con límites de confianza del 95%.
Represente el ajuste de sf junto con una gráfica de dispersión de los datos.
plot(sf,[x,y],z)
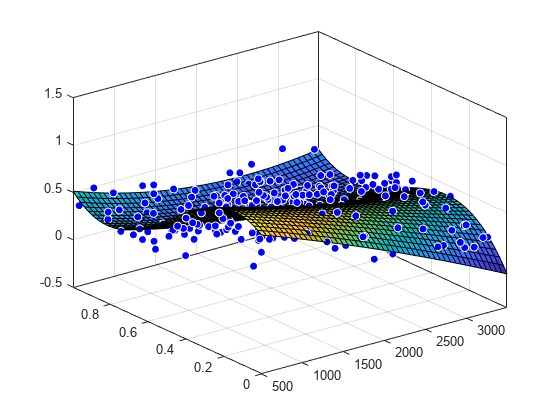
Cargue los datos franke y conviértalos en una tabla de MATLAB®.
load franke
T = table(x,y,z);Especifique las variables en la tabla como entradas de la función fit y represente el ajuste.
f = fit([T.x, T.y],T.z,'linearinterp');
plot( f, [T.x, T.y], T.z )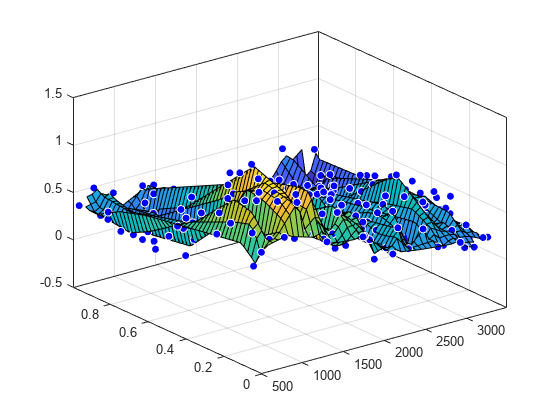
Cargue y represente los datos, cree opciones de ajuste y tipo de ajuste con las funciones fittype y fitoptions, luego, cree y represente el ajuste.
Cargue y represente los datos en census.mat.
load census plot(cdate,pop,'o')

Cree un objeto de opciones de ajuste y un tipo de ajuste para el modelo personalizado no lineal , en el que a y b son coeficientes y n es un parámetro dependiente de problema.
fo = fitoptions('Method','NonlinearLeastSquares',... 'Lower',[0,0],... 'Upper',[Inf,max(cdate)],... 'StartPoint',[1 1]); ft = fittype('a*(x-b)^n','problem','n','options',fo);
Ajuste los datos con las opciones de ajuste y un valor de n = 2.
[curve2,gof2] = fit(cdate,pop,ft,'problem',2)curve2 =
General model:
curve2(x) = a*(x-b)^n
Coefficients (with 95% confidence bounds):
a = 0.006092 (0.005743, 0.006441)
b = 1789 (1784, 1793)
Problem parameters:
n = 2
gof2 = struct with fields:
sse: 246.1543
rsquare: 0.9980
dfe: 19
adjrsquare: 0.9979
rmse: 3.5994
Ajuste los datos con las opciones de ajuste y un valor de n = 3.
[curve3,gof3] = fit(cdate,pop,ft,'problem',3)curve3 =
General model:
curve3(x) = a*(x-b)^n
Coefficients (with 95% confidence bounds):
a = 1.359e-05 (1.245e-05, 1.474e-05)
b = 1725 (1718, 1731)
Problem parameters:
n = 3
gof3 = struct with fields:
sse: 232.0058
rsquare: 0.9981
dfe: 19
adjrsquare: 0.9980
rmse: 3.4944
Represente los resultados de ajuste con los datos.
hold on plot(curve2,'m') plot(curve3,'c') legend('Data','n=2','n=3') hold off

Cargue el conjunto de datos de muestra de reacción nuclear carbon12alpha.
load carbon12alphaangle es un vector de ángulos de emisión en radianes. counts es un vector de recuentos brutos de partículas alfa que corresponden a los ángulos en angle.
Represente una gráfica de dispersión de los recuentos en función de los ángulos.
scatter(angle,counts)
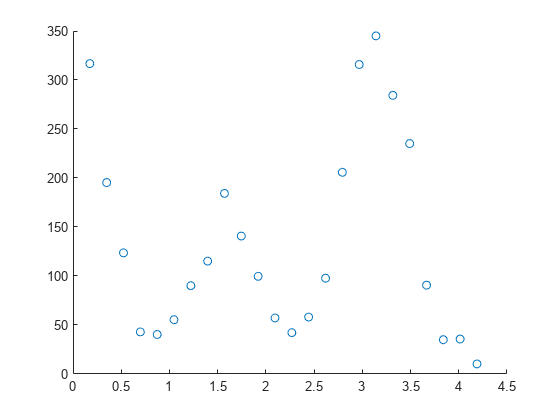
La gráfica de dispersión muestra que los recuentos oscilan a medida que el ángulo aumenta entre 0 y 4.5. Para ajustar un modelo polinómico a los datos, especifique el argumento de entrada fitType como "poly#", donde # es un entero de uno a nueve. Puede ajustar modelos de hasta nueve grados. Para obtener más información, consulte Lista de modelos de biblioteca para ajuste de curvas y de superficie.
Ajuste un polinomio de quinto grado, séptimo grado y noveno grado a los datos de reacción nuclear. Devuelva los valores estadísticos de bondad de ajuste para cada ajuste.
[f5,gof5] = fit(angle,counts,"poly5"); [f7,gof7] = fit(angle,counts,"poly7"); [f9,gof9] = fit(angle,counts,"poly9");
Genere un vector de puntos de consulta entre 0 y 4.5 mediante la función linspace. Evalúe los ajustes polinomiales en los puntos de consulta y, a continuación, represéntelos junto con los datos de reacción nuclear.
xq = linspace(0,4.5,1000); figure hold on scatter(angle,counts,"k") plot(xq,f5(xq)) plot(xq,f7(xq)) plot(xq,f9(xq)) ylim([-100,550]) legend("original data","fifth-degree polynomial","seventh-degree polynomial","ninth-degree polynomial")

La gráfica indica que el polinomio de noveno grado es el que mejor se ajusta a los datos.
Represente los valores estadísticos de bondad de ajuste para cada ajuste mediante la función struct2table.
gof = struct2table([gof5 gof7 gof9],RowNames=["f5" "f7" "f9"])
gof=3×5 table
sse rsquare dfe adjrsquare rmse
__________ _______ ___ __________ ______
f5 1.0901e+05 0.54614 18 0.42007 77.82
f7 32695 0.86387 16 0.80431 45.204
f9 3660.2 0.98476 14 0.97496 16.169
La suma del error cuadrático (SSE, por sus siglas en inglés) del ajuste polinomial de noveno grado es menor que las SSE de los ajustes de quinto y séptimo grado. Este resultado confirma que el polinomio de noveno grado es el que mejor se ajusta a los datos.
Cargue el conjunto de datos de muestra census. Ajuste un polinomio cúbico y especifique las opciones de ajuste Normalize (centro y escala) y Robust.
load census; f = fit(cdate,pop,'poly3','Normalize','on','Robust','Bisquare')
f =
Linear model Poly3:
f(x) = p1*x^3 + p2*x^2 + p3*x + p4
where x is normalized by mean 1890 and std 62.05
Coefficients (with 95% confidence bounds):
p1 = -0.4619 (-1.895, 0.9707)
p2 = 25.01 (23.79, 26.22)
p3 = 77.03 (74.37, 79.7)
p4 = 62.81 (61.26, 64.37)
Represente el ajuste.
plot(f,cdate,pop)
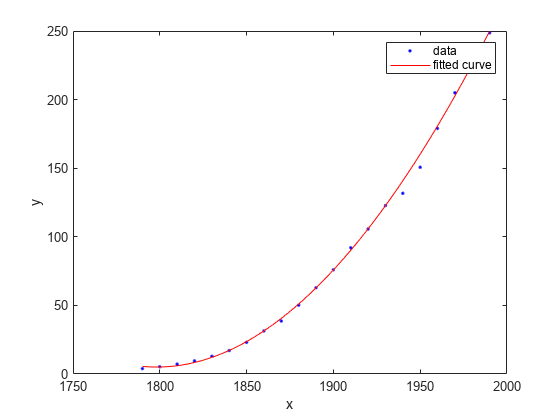
Defina una función en un archivo y utilícela para crear un tipo de ajuste y ajustar una curva.
Defina una función en un archivo de MATLAB®.
function y = piecewiseLine(x,a,b,c,d,k) % PIECEWISELINE A line made of two pieces % that is not continuous. y = zeros(size(x)); % This example includes a for-loop and if statement % purely for example purposes. for i = 1:length(x) if x(i) < k, y(i) = a + b.* x(i); else y(i) = c + d.* x(i); end end end
Guarde el archivo.
Defina algunos datos, cree un tipo de ajuste especificando la función piecewiseLine, cree un ajuste con el tipo de ajuste ft y represente los resultados.
x = [0.81;0.91;0.13;0.91;0.63;0.098;0.28;0.55;... 0.96;0.96;0.16;0.97;0.96]; y = [0.17;0.12;0.16;0.0035;0.37;0.082;0.34;0.56;... 0.15;-0.046;0.17;-0.091;-0.071]; ft = fittype( 'piecewiseLine( x, a, b, c, d, k )' ) f = fit( x, y, ft, 'StartPoint', [1, 0, 1, 0, 0.5] ) plot( f, x, y )
Cargue algunos datos y ajuste una ecuación personalizada que especifique los puntos que se deben excluir. Represente los resultados.
Cargue datos y defina una ecuación personalizada y algunos puntos de partida.
[x, y] = titanium;
gaussEqn = 'a*exp(-((x-b)/c)^2)+d'gaussEqn = 'a*exp(-((x-b)/c)^2)+d'
startPoints = [1.5 900 10 0.6]
startPoints = 1×4
1.5000 900.0000 10.0000 0.6000
Cree dos ajustes con la ecuación personalizada y los puntos de partida, y defina dos conjuntos distintos de puntos excluidos utilizando un vector índice y una expresión. Utilice Exclude para eliminar los valores atípicos de su ajuste.
f1 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', [1 10 25])
f1 =
General model:
f1(x) = a*exp(-((x-b)/c)^2)+d
Coefficients (with 95% confidence bounds):
a = 1.493 (1.432, 1.554)
b = 897.4 (896.5, 898.3)
c = 27.9 (26.55, 29.25)
d = 0.6519 (0.6367, 0.6672)
f2 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', x < 800)
f2 =
General model:
f2(x) = a*exp(-((x-b)/c)^2)+d
Coefficients (with 95% confidence bounds):
a = 1.494 (1.41, 1.578)
b = 897.4 (896.2, 898.7)
c = 28.15 (26.22, 30.09)
d = 0.6466 (0.6169, 0.6764)
Represente ambos ajustes.
plot(f1,x,y)
title('Fit with data points 1, 10, and 25 excluded')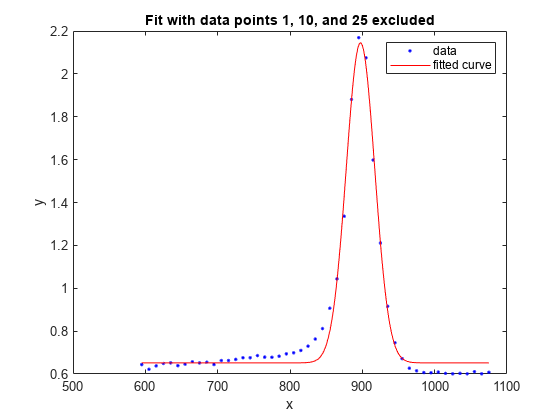
figure
plot(f2,x,y)
title('Fit with data points excluded such that x < 800')
Puede definir los puntos excluidos como variables antes de proporcionarlos como entradas para la función de ajuste. Los siguientes pasos recrean los ajustes del ejemplo anterior y le permiten representar los puntos excluidos, así como los datos y el ajuste.
Cargue datos y defina una ecuación personalizada y algunos puntos de partida.
[x, y] = titanium;
gaussEqn = 'a*exp(-((x-b)/c)^2)+d'gaussEqn = 'a*exp(-((x-b)/c)^2)+d'
startPoints = [1.5 900 10 0.6]
startPoints = 1×4
1.5000 900.0000 10.0000 0.6000
Defina dos conjuntos de puntos para excluir, utilizando un vector índice y una expresión.
exclude1 = [1 10 25]; exclude2 = x < 800;
Cree dos ajustes con la ecuación personalizada, puntos de partida y los dos puntos excluidos distintos.
f1 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', exclude1); f2 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', exclude2);
Represente ambos ajustes y destaque los datos excluidos.
plot(f1,x,y,exclude1)
title('Fit with data points 1, 10, and 25 excluded')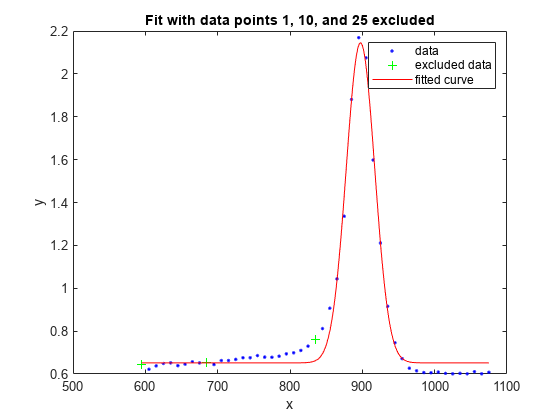
figure;
plot(f2,x,y,exclude2)
title('Fit with data points excluded such that x < 800')
Para generar un ejemplo de ajuste de superficie con puntos excluidos, cargue algunos datos de superficie y cree y represente ajustes que especifiquen los datos excluidos.
load franke f1 = fit([x y],z,'poly23', 'Exclude', [1 10 25]); f2 = fit([x y],z,'poly23', 'Exclude', z > 1); figure plot(f1, [x y], z, 'Exclude', [1 10 25]); title('Fit with data points 1, 10, and 25 excluded')
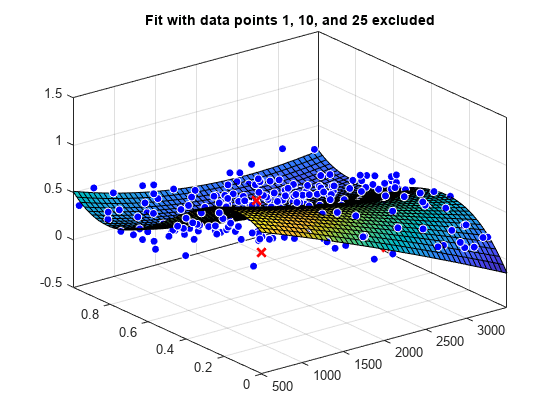
figure plot(f2, [x y], z, 'Exclude', z > 1); title('Fit with data points excluded such that z > 1')
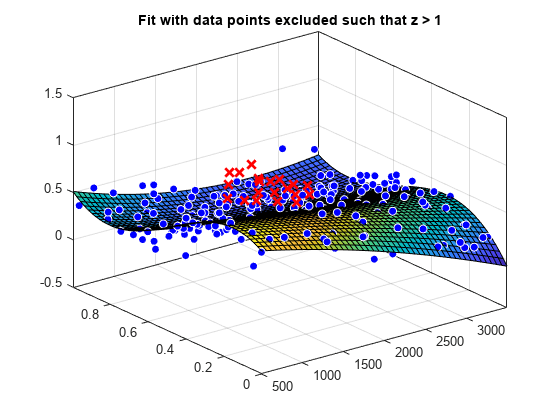
Genere algunos datos ruidosos utilizando las funciones membrane y randn.
n = 41; M = membrane(1,20)+0.02*randn(n); [X,Y] = meshgrid(1:n);
La matriz M contiene los datos de la membrana en forma de L con ruido añadido. Las matrices X e Y contienen los valores de los índices de fila y columna, respectivamente, de los elementos correspondientes de M.
Muestre una gráfica de superficie de los datos.
figure(1) surf(X,Y,M)

La gráfica muestra una membrana arrugada en forma de L. Las arrugas de la membrana se deben al ruido de los datos.
Ajuste dos superficies a través de la membrana arrugada mediante interpolación lineal. Para la primera superficie, especifique el método de extrapolación lineal. Para la segunda superficie, especifique el método de extrapolación como vecino más próximo.
flinextrap = fit([X(:),Y(:)],M(:),"linearinterp",ExtrapolationMethod="linear"); fnearextrap = fit([X(:),Y(:)],M(:),"linearinterp",ExtrapolationMethod="nearest");
Analice las diferencias entre los métodos de extrapolación utilizando la función meshgrid para evaluar los ajustes en los puntos de consulta que se extienden más allá de la envolvente convexa de los datos X e Y.
[Xq,Yq] = meshgrid(-10:50); Zlin = flinextrap(Xq,Yq); Znear = fnearextrap(Xq,Yq);
Represente los ajustes evaluados.
figure(2) surf(Xq,Yq,Zlin) title("Linear Extrapolation") xlabel("X") ylabel("Y") zlabel("M")
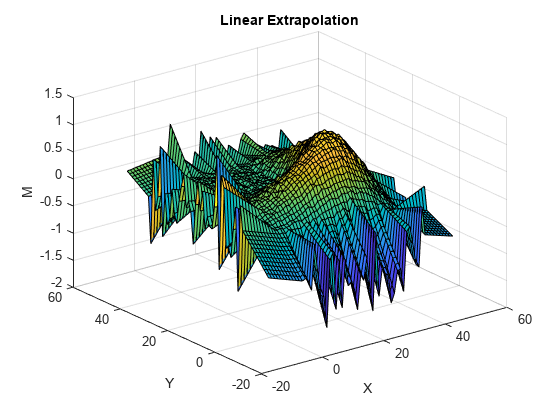
figure(3) surf(Xq,Yq,Znear) title("Nearest Neighbor Extrapolation") xlabel("X") ylabel("Y") zlabel("M")

El método de extrapolación lineal genera picos fuera de la envolvente convexa. Los segmentos del plano que forman los picos siguen el gradiente en los puntos del borde de la envolvente convexa. El método de extrapolación por el vecino más cercano utiliza los datos del borde para ampliar la superficie en cada dirección. Este método de extrapolación genera ondas que imitan el borde.
Ajuste una curva de spline de suavizado y devuelva estadísticas sobre bondad de ajuste e información sobre el algoritmo de ajuste.
Cargue el conjunto de datos de muestra enso. El conjunto de datos de muestra enso contiene datos para las diferencias de presión atmosférica promediadas mensuales entre la Isla de Pascua y Darwin, Australia.
load enso;Ajuste una curva de spline de suavizado a los datos de month y pressure, y devuelva estadísticas de bondad de ajuste y la estructura output.
[curve,gof,output] = fit(month,pressure,"smoothingspline");Represente la curva ajustada con los datos utilizados para ajustar la curva.
plot(curve,month,pressure); xlabel("Month"); ylabel("Pressure");

Represente los valores residuales en comparación con los datos de x (month).
plot(curve,month,pressure,"residuals") xlabel("Month") ylabel("Residuals")
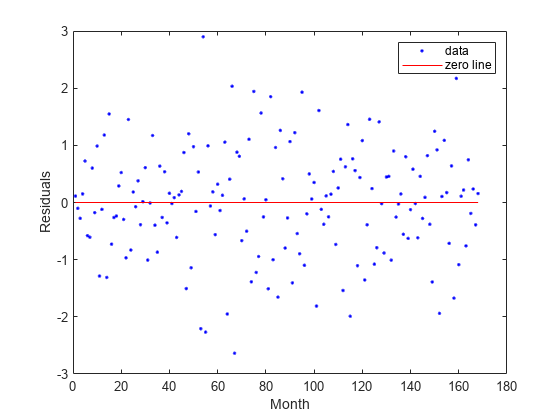
Utilice los datos residuals de la estructura output para representar los valores residuales en comparación con los datos en y (pressure). Para acceder al campo residuals de output, utilice notación de puntos.
residuals = output.residuals; plot( pressure,residuals,".") xlabel("Pressure") ylabel("Residuals")
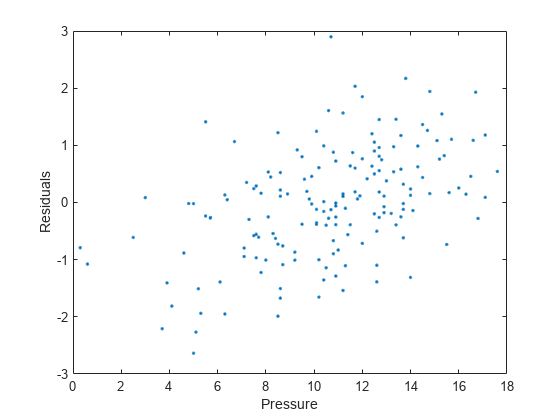
Genere datos con tendencia exponencial y luego ajústelos con la primera ecuación de la curva de ajuste de la biblioteca de modelos exponenciales (exponencial de un solo término). Represente los resultados.
x = (0:0.2:5)';
y = 2*exp(-0.2*x) + 0.5*randn(size(x));
f = fit(x,y,'exp1');
plot(f,x,y)
Puede utilizar funciones anónimas para hacer que sea más fácil pasar otros datos a la función fit.
Cargue los datos y establezca Emax en 1 antes de definir la función anónima:
data = importdata( 'OpioidHypnoticSynergy.txt' );
Propofol = data.data(:,1);
Remifentanil = data.data(:,2);
Algometry = data.data(:,3);
Emax = 1;Defina la ecuación modelo como una función anónima:
Effect = @(IC50A, IC50B, alpha, n, x, y) ... Emax*( x/IC50A + y/IC50B + alpha*( x/IC50A )... .* ( y/IC50B ) ).^n ./(( x/IC50A + y/IC50B + ... alpha*( x/IC50A ) .* ( y/IC50B ) ).^n + 1);
Utilice la función anónima Effect como entrada para la función fit y represente los resultados:
AlgometryEffect = fit( [Propofol, Remifentanil], Algometry, Effect, ... 'StartPoint', [2, 10, 1, 0.8], ... 'Lower', [-Inf, -Inf, -5, -Inf], ... 'Robust', 'LAR' ) plot( AlgometryEffect, [Propofol, Remifentanil], Algometry )
Para ver más ejemplos de uso de funciones anónimas y otros modelos personalizados para ajuste, consulte la función fittype.
Para las propiedades Upper, Lower y StartPoint, debe encontrar el orden de las entradas para los coeficientes.
Cree un tipo de ajuste.
ft = fittype('b*x^2+c*x+a');Obtenga los nombres y el orden de los coeficientes con la función coeffnames.
coeffnames(ft)
ans = 3x1 cell
{'a'}
{'b'}
{'c'}
Tenga en cuenta que es distinto al orden de coeficientes en la expresión utilizada para crear ft con fittype.
Cargue los datos, cree un ajuste y defina los puntos de partida.
load enso fit(month,pressure,ft,'StartPoint',[1,3,5])
ans =
General model:
ans(x) = b*x^2+c*x+a
Coefficients (with 95% confidence bounds):
a = 10.94 (9.362, 12.52)
b = 0.0001677 (-7.985e-05, 0.0004153)
c = -0.0224 (-0.06559, 0.02079)
Esto asigna un valor inicial a los coeficientes de la siguiente manera: a = 1, b = 3, c = 5.
También puede obtener opciones de ajuste y definir puntos iniciales y límites inferiores y luego reajustar con las nuevas opciones.
options = fitoptions(ft)
options =
nlsqoptions with properties:
StartPoint: []
Lower: []
Upper: []
Algorithm: 'Trust-Region'
DiffMinChange: 1.0000e-08
DiffMaxChange: 0.1000
Display: 'Notify'
MaxFunEvals: 600
MaxIter: 400
TolFun: 1.0000e-06
TolX: 1.0000e-06
Robust: 'Off'
Normalize: 'off'
Exclude: []
Weights: []
Method: 'NonlinearLeastSquares'
options.StartPoint = [10 1 3]; options.Lower = [0 -Inf 0]; fit(month,pressure,ft,options)
ans =
General model:
ans(x) = b*x^2+c*x+a
Coefficients (with 95% confidence bounds):
a = 10.23 (9.448, 11.01)
b = 4.335e-05 (-1.82e-05, 0.0001049)
c = 5.523e-12 (fixed at bound)
Argumentos de entrada
Datos que ajustar, especificados como una matriz con una (ajuste de curva) o dos (ajuste de superficie) columnas. Puede especificar variables en una tabla de MATLAB con tablename.varname. No puede contener Inf ni NaN. En el ajuste solo se utilizan las partes reales de datos complejos.
Ejemplo: x
Ejemplo: [x,y]
Tipos de datos: double
Datos que ajustar, especificados como vector columna con el mismo número de filas que x. Puede especificar una variable en una tabla de MATLAB con tablename.varname. No puede contener Inf ni NaN. En el ajuste solo se utilizan las partes reales de datos complejos.
Utilice prepareCurveData o prepareSurfaceData si sus datos no están en forma de vector columna.
Tipos de datos: double
Datos que ajustar, especificados como vector columna con el mismo número de filas que x. Puede especificar una variable en una tabla de MATLAB con tablename.varname. No puede contener Inf ni NaN. En el ajuste solo se utilizan las partes reales de datos complejos.
Utilice prepareSurfaceData si sus datos no están en forma de vector columna. Por ejemplo, si tiene tres matrices o si sus datos están en forma de vector cuadrícula, en donde length(X) = n, length(Y) = m y size(Z) = [m,n].
Tipos de datos: double
Tipo de modelo para el ajuste, especificado como un vector de caracteres o escalar de cadena que representa un nombre de modelo de biblioteca o una expresión de MATLAB, un arreglo de cadenas de términos de modelos lineales o un arreglo de celdas de vectores de caracteres de tales términos, una función anónima o un fittype creado con la función fittype. Puede utilizar cualquiera de las primeras entradas válidas para fittype como entrada para fit.
Para ver una lista de nombres de modelos de biblioteca, consulte Nombres y ecuaciones de modelos.
Para ajustar un modelo personalizado, utilice una expresión de MATLAB, un arreglo de celdas de términos de modelo lineales o una función anónima. También puede crear un fittype mediante la función fittype y, a continuación, utilizarlo como valor del argumento de entrada fitType. Para ver un ejemplo, consulte Ajustar un modelo personalizado con una función anónima. Para ver ejemplos que usan términos de modelos lineales, consulte la función fittype.
Ejemplo: "poly2"
Opciones de algoritmos construidas con la función fitoptions. Se trata de una alternativa para especificar argumentos de par nombre-valor en opciones de ajuste.
Argumentos de par nombre-valor
Especifique pares de argumentos opcionales Name1=Value1,...,NameN=ValueN, donde Name es el nombre del argumento y Value el valor correspondiente. Los argumentos nombre-valor deben aparecer tras otros argumentos, aunque no importa el orden de los pares.
En versiones anteriores a R2021a, utilice comas para separar cada nombre y valor, y encierre Name entre comillas.
Ejemplo: Lower=[0,0],Upper=[Inf,max(x)],StartPoint=[1 1] especifica el método de ajuste, límites y puntos de partida.
Opciones para todos los métodos de ajuste
Opción para centrar y escalar datos, especificada como el par separado por comas compuesto por 'Normalize' y 'on' u 'off'.
Tipos de datos: char
Puntos que excluir del ajuste, especificados como el par separado por comas compuesto por 'Exclude' y uno de los siguientes:
Una expresión que describe un vector lógico, por ejemplo,
x > 10.Un vector de enteros que indexa los puntos que quiere excluir, por ejemplo,
[1 10 25].Un vector lógico para todos los puntos de datos, donde
truerepresenta un valor atípico, creado porexcludedata.
Para ver un ejemplo, consulte Excluir puntos del ajuste.
Tipos de datos: logical | double
Valores que asignar a constantes dependientes de problemas, especificados como el par separado por comas compuesto por 'problem' y un arreglo de celdas con un elemento por constante dependiente de problemas. Para obtener más detalles, consulte fittype.
Tipos de datos: cell | double
Opciones de suavizado
Parámetro de suavizado, especificado como el par separado por comas compuesto por 'SmoothingParam' y un valor escalar entre 0 y 1. El valor predeterminado depende del conjunto de datos. Solo disponible si el tipo de ajuste es smoothingspline.
Tipos de datos: double
Proporción de puntos de datos que utilizar en regresiones locales, especificada como el par separado por comas compuesto por 'Span' y un valor escalar entre 0 y 1. Solo disponible si el tipo de ajuste es lowess o loess.
Tipos de datos: double
Opciones de interpolación
Método de extrapolación para un ajuste de interpolación, especificado como uno de los siguientes valores.
| Valor | Descripción | Ajustes admitidos |
|---|---|---|
"auto" | Valor predeterminado para todos los tipos de ajuste de interpolación. Establezca | Todos los tipos de ajuste de interpolación y ajustes de curva |
"none" | Sin extrapolación. Los puntos de consulta fuera de la envolvente convexa de los datos de ajuste se evalúan en | Ajustes de curva: Ajustes de curva y de superficie: |
"linear" | Extrapolación lineal basada en gradientes de límite. | Ajustes de superficie: Ajustes de curva y de superficie: |
"nearest" | Extrapolación por el vecino más cercano. Este método evalúa el valor del punto más cercano en el límite de la envolvente convexa de los datos de ajuste.
| Ajustes de curva: Ajustes de curva y de superficie: |
"thinplate" | Extrapolación por spline de thin-plate. Este método amplía la interpolación por spline de thin-plate hasta más allá de la envolvente convexa de los datos de ajuste. Para obtener más información, consulte | Ajustes de superficie: |
"biharmonic" | Extrapolación por spline biarmónico. Este método amplía la interpolación por spline biarmónico hasta más allá de la envolvente convexa de los datos de ajuste. | Ajustes de superficie: |
"pchip" | Extrapolación por PCHIP (interpolación cúbica por tramos de Hermite). Este método amplía una PCHIP que conserva la forma fuera de la envolvente convexa de los datos de ajuste. Para obtener más información, consulte | Ajustes de curva: |
"cubic" | Extrapolación por spline cúbico. Este método amplía una interpolación por spline cúbico hasta más allá de la envolvente convexa de los datos de ajuste.
| Ajustes de curva: |
Tipos de datos: char | string
Opciones de mínimos cuadrados lineales y no lineales
Método de ajuste robusto de mínimos cuadrados lineales, especificado como el par separado por comas compuesto por 'Robust' y uno de estos valores:
'LAR'especifica el método de mínimo residual absoluto.'Bisquare'especifica el método de ponderaciones bicuadradas.
Disponible cuando el Method del tipo de ajuste es LinearLeastSquares o NonlinearLeastSquares.
Tipos de datos: char
Límites inferiores de coeficientes que ajustar, especificados como el par separado por comas compuesto por 'Lower' y un vector. El valor predeterminado es un vector vacío, que indica que el ajuste no está restringido por límites inferiores. Si se especifican los límites, la longitud del vector debe ser igual al número de coeficientes. Encuentre el orden de las entradas para los coeficientes en el valor del vector con la función coeffnames. Para ver un ejemplo, consulte Encontrar el orden de coeficientes para definir puntos de partida y límites. Los límites inferiores individuales sin restringir se pueden especificar con -Inf.
Disponible cuando el Method es LinearLeastSquares o NonlinearLeastSquares.
Tipos de datos: double
Límites superiores de coeficientes que ajustar, especificados como el par separado por comas compuesto por 'Upper' y un vector. El valor predeterminado es un vector vacío, que indica que el ajuste no está restringido por límites superiores. Si se especifican los límites, la longitud del vector debe ser igual al número de coeficientes. Encuentre el orden de las entradas para los coeficientes en el valor del vector con la función coeffnames. Para ver un ejemplo, consulte Encontrar el orden de coeficientes para definir puntos de partida y límites. Los límites superiores individuales sin restringir se pueden especificar con +Inf.
Disponible cuando el Method es LinearLeastSquares o NonlinearLeastSquares.
Tipos de datos: logical
Opciones de mínimos cuadrados no lineales
Valores iniciales para los coeficientes, especificados como el par separado por comas compuesto por 'StartPoint' y un vector. Encuentre el orden de las entradas para los coeficientes en el valor del vector con la función coeffnames. Para ver un ejemplo, consulte Encontrar el orden de coeficientes para definir puntos de partida y límites.
Si no se trasladan puntos de partida (el valor predeterminado de un vector vacío) a la función fit, los puntos de partida para algunos modelos de biblioteca se determinan de forma heurística. Para modelos racionales y de Weibull, y todos los modelos personalizados no lineales, la toolbox selecciona los valores iniciales predeterminados para los coeficientes de forma uniforme y aleatoria del intervalo (0,1). Como resultado, varios ajustes con los mismos datos y modelo podrían derivar en distintos coeficientes ajustados. Para evitarlo, especifique valores iniciales para coeficientes con un objeto fitoptions o con un valor del vector para el valor StartPoint.
Disponible cuando el Method es NonlinearLeastSquares.
Tipos de datos: double
Algoritmo que utilizar en el proceso de ajuste, especificado como el par separado por comas compuesto por 'Algorithm' y 'Levenberg-Marquardt' o 'Trust-Region'.
Disponible cuando el Method es NonlinearLeastSquares.
Tipos de datos: char
Cambio máximo en los coeficientes para gradientes de diferencias finitas, especificado como el par separado por comas compuesto por 'DiffMaxChange' y un escalar.
Disponible cuando el Method es NonlinearLeastSquares.
Tipos de datos: double
Cambio mínimo en los coeficientes para gradientes de diferencias finitas, especificado como el par separado por comas compuesto por 'DiffMinChange' y un escalar.
Disponible cuando el Method es NonlinearLeastSquares.
Tipos de datos: double
Opción de visualizar en la ventana de comandos, especificada como el par separado por comas compuesto por 'Display' y una de estas opciones:
'notify'solo muestra salidas si el ajuste no converge.'final'solo muestra la salida final.'iter'muestra la salida en cada iteración.'off'no muestra salida alguna.
Disponible cuando el Method es NonlinearLeastSquares.
Tipos de datos: char
Número máximo de evaluaciones de modelo permitidas, especificado como el par separado por comas compuesto por 'MaxFunEvals' y un escalar.
Disponible cuando el Method es NonlinearLeastSquares.
Tipos de datos: double
Número máximo de iteraciones permitidas para el ajuste, especificado como el par separado por comas compuesto por 'MaxIter' y un escalar.
Disponible cuando el Method es NonlinearLeastSquares.
Tipos de datos: double
Tolerancia de terminación en el valor del modelo, especificada como el par separado por comas compuesto por 'TolFun' y un escalar.
Disponible cuando el Method es NonlinearLeastSquares.
Tipos de datos: double
Tolerancia de terminación en los valores de coeficiente, especificada como el par separado por comas compuesto por 'TolX' y un escalar.
Disponible cuando el Method es NonlinearLeastSquares.
Tipos de datos: double
Argumentos de salida
Resultado de ajuste, devuelto como objeto cfit (para curvas) o sfit (para superficies). Consulte Posprocesar ajustes para ver funciones de representación, evaluación, cálculo de intervalos de confidencia, integración, diferenciación o modificación de su objeto de ajuste.
Estadísticas de bondad de ajuste, devueltas como la estructura gof incluidos los valores de esta tabla.
Campo | Valor |
|---|---|
| Suma de cuadrados debidos al error |
| R-cuadrado (coeficiente de determinación) |
| Grados de libertad en el error |
| Coeficiente de determinación ajustado al grado de libertad |
| Raíz del error cuadrático medio (error estándar) |
Ejemplo: gof.rmse
Información del algoritmo de ajuste, devuelto como la estructura output que contiene información asociada con el algoritmo de ajuste.
Los campos dependen del algoritmo. Por ejemplo, la estructura output para algoritmos de mínimos cuadrados no lineales incluye los campos que se muestran en esta tabla.
Campo | Valor |
|---|---|
| Número de observaciones (valores de respuesta) |
| Número de parámetros desconocidos (coeficientes) que ajustar |
| Vector de valores residuales brutos (valores observados menos valores ajustados) |
| Matriz jacobiana |
| Describe la condición de salida del algoritmo. Los indicadores positivos señalan convergencia dentro de las tolerancias. Los indicadores cero señalan que el número máximo de evaluaciones de función o de iteraciones se ha superado. Los indicadores negativos señalan que el algoritmo no ha convergido a una solución. |
| Número de iteraciones |
| Número de evaluaciones de función |
| Medida de optimalidad de primer orden (máximo absoluto de componentes de gradiente) |
| Algoritmo de ajuste utilizado |
Ejemplo: output.Jacobian
Historial de versiones
Introducido antes de R2006aA partir de la versión 2023b, puede especificar métodos de extrapolación adicionales para los ajustes de interpolación de curva utilizando el argumento de par nombre-valor ExtrapolationMethod. Para obtener más información, consulte Extrapolation for Interpolant Fit Types.
A partir de la versión R2023b, puede especificar los tipos de ajuste sigmoide y logarítmico para los ajustes de curva. Para obtener más información, consulte Lista de modelos de biblioteca para ajuste de curvas y de superficie.
A partir de la versión 2023a, puede especificar el método de extrapolación para los ajustes de interpolación utilizando el argumento de par nombre-valor ExtrapolationMethod. Para los ajustes de curvas, Curve Fitting Toolbox™ solo admite los métodos de extrapolación predeterminados disponibles en versiones anteriores.
Consulte también
Apps
Funciones
fittype|fitoptions|prepareCurveData|prepareSurfaceData|feval|plot|confint
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)