Gráfico de factores para SLAM

Esta página se ha traducido mediante traducción automática. Haga clic aquí para ver la última versión en inglés.

Gráfico de factores para SLAM

En el contexto de la localización y el mapeo simultáneos (SLAM), un gráfico de factores es una herramienta para estimar los estados más probables de un robot y puntos de referencia mediante la integración de datos de múltiples sensores como sensores LiDAR , sensores IMU, sensores GPS y cámaras. Esta fusión de múltiples sensores mejora la precisión y la robustez de la estimación del estado.

Estructuralmente, un gráfico factorial es un gráfico bipartito, lo que significa que consta de dos tipos de elementos:

Nodos: los nodos representan las variables del problema, como el estado del robot o vehículo y la posición de los puntos de referencia en el entorno. En los gráficos conceptuales, los nodos se muestran como círculos.
Para obtener una lista de los tipos de nodos admitidos actualmente y su formato de estado, consulte la sección Tipos de nodos.
Factores — Los factores representan las relaciones o funciones que definen las dependencias entre los nodos, generalmente utilizando mediciones de sensores. En los gráficos conceptuales, los factores se muestran como cuadrados. Para obtener más información sobre los factores, consulte la sección Factores.
Para obtener una lista de los factores admitidos actualmente, consulte la sección Lista de factores admitidos.

En Navigation Toolbox™, puedes construir gráficos factoriales utilizando el objeto factorGraph.

Visualizaciones de gráficos de factores

Puede visualizar un gráfico de factores de forma espacial o conceptual. Para mostrar las diferencias, considere el gráfico factorial de este código.

fg = factorGraph;
ids = generateNodeID(fg,3,"factorTwoPoseSE2");
f = factorTwoPoseSE2(ids,Measurement=relMeasure,Information=infoMatrix); % Measurements for factorTwoPoseSE2 factor are odometry sensor data
addFactor(fg,f);
nodeState(fg,unique(ids),initPoseGuess) % Set initial state guesses of pose nodes

Visualización conceptual

La visualización conceptual se centra en la relación entre los nodos y los factores en el gráfico y deja clara la calidad bipartita del gráfico factorial. La posición de los nodos y factores en el gráfico no proporciona ninguna información sobre su estado actual. Los nodos se representan como círculos y los factores se representan como cuadrados. Esta figura muestra el gráfico conceptual del gráfico factorial previamente definido, fg.

Conceptual visualization of factor graph containing four SE(2) pose nodes connected by three factors.

Los factores se definen como cuadrados naranjas con su ID de factor único indicado dentro del factor y el tipo de factor definido debajo del factor.

Los nodos se definen como círculos con su ID de nodo único indicado dentro del nodo y el tipo de nodo definido debajo del nodo. Este gráfico conceptual contiene solo nodos de pose, pero los gráficos conceptuales pueden contener tres tipos de nodos:

Los nodos de pose son azules y representan nodos de pose SE(2) o SE(3).
Los nodos de referencia son de color púrpura y representan los puntos xy y xyz.
Los nodos no espaciales son verdes y representan cantidades que no se pueden representar en el espacio físico, como la velocidad 3D y los sesgos del giroscopio y del acelerómetro de la IMU.

Legend for conceptual graph.

Visualización espacial

Las visualizaciones espaciales muestran el estado de los nodos de pose y las posiciones de los puntos de referencia entre sí. Los nodos no espaciales, como la velocidad 3D y los sesgos del giroscopio y del acelerómetro de la IMU, no aparecen en esta visualización.

Esta figura muestra la visualización espacial del gráfico de factores previamente definido.

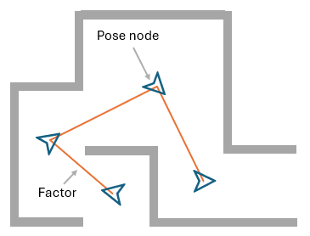
Spatial visualization of factor graph containing four SE(2) pose nodes connected by three factors.

Puede utilizar la función de objeto show para trazar una visualización espacial de un gráfico de factores en MATLAB^®.

Modelo probabilístico

Los gráficos de factores proporcionan una forma estructurada de gestionar la incertidumbre al representar la distribución de probabilidad conjunta sobre los estados del robot, las posiciones de los puntos de referencia y las mediciones de los sensores. Al descomponer esta distribución en factores locales más simples, los gráficos de factores pueden representar las dependencias entre estas variables. Esto le permite fusionar diferentes mediciones de sensores, como datos IMU y GPS, para mejorar la precisión de las estimaciones de estado a través de la optimización iterativa.

Factores

En un gráfico factorial, los factores actúan como bordes que conectan nodos, lo que indica la relación entre las variables del problema. Al ser un modelo probabilístico, el gráfico de factores aprovecha estas relaciones para gestionar la incertidumbre y optimizar soluciones utilizando datos de múltiples fuentes, como sensores IMU y GPS. Esta estructura permite la integración y el procesamiento eficiente de diversas entradas de sensores para estimar con precisión las variables de interés.

Los factores también pueden verse como restricciones sobre los nodos, donde el costo de una restricción indica qué tan bien se alinea el estado del nodo con los valores del mundo real. Por ejemplo, en un robot con sensores de odometría, GPS e IMU, cada sensor afirma información observada sobre el estado del nodo de pose, y estas restricciones acumulativamente conforman un costo total. Un costo total bajo sugiere una alta probabilidad de que la estimación estatal coincida con el estado real. Por el contrario, un costo alto indica una discrepancia entre la estimación del estado y el estado real, lo que requiere que el optimizador ajuste la estimación del estado. Este proceso iterativo garantiza que el robot determine con precisión su posición y orientación.

Derechos residuales de autor

El costo asociado con los factores en el gráfico de factores se deriva de los residuales, que son las diferencias entre las lecturas esperadas del sensor, basadas en la estimación del estado actual, y las lecturas reales del sensor. El gráfico de factores modela el problema como un problema de mínimos cuadrados no lineal para minimizar los residuales y refinar las estimaciones de los estados del robot y del punto de referencia. Los residuos provienen de errores en las mediciones del sensor o imprecisiones en el modelo de movimiento. El proceso de optimización ajusta iterativamente las estimaciones de estado para lograr el mejor ajuste posible a los datos.

Por ejemplo, el factor factorTwoPoseSE2 calcula los residuales utilizando este proceso usando esta información:

$p o s e_{i} = [\begin{matrix} x_{i} \\ y_{i} \\ θ_{i} \end{matrix}]$ , $p o s e_{j} = [\begin{matrix} x_{j} \\ y_{j} \\ θ_{j} \end{matrix}]$ — Estimaciones de estado del nodo de pose anterior i y del nodo de pose actual j. Tenga en cuenta que puede consultar el gráfico de factores para la estimación del estado de los nodos utilizando la función de objeto nodeState.
$p o s e_{m} = [\begin{matrix} x_{m} \\ y_{m} \\ θ_{m} \end{matrix}]$ — Estado de pose medido. Tenga en cuenta que los datos de medición de los factores provienen de sensores en el robot.
$I = [\begin{matrix} I_{x x} & I_{x y} & I_{x θ} \\ I_{x y} & I_{y y} & I_{y θ} \\ I_{θ x} & I_{θ y} & I_{θ θ} \end{matrix}]$ — Matriz de información que describe la precisión y el sesgo de la pose medida por el sensor.

Entonces el proceso para calcular los residuales para un factor factorTwoPoseSE2 es:

Calcule los residuales para la posición xy creando una matriz de rotación SO(2) a partir de la orientación anterior θ_i. Transponga esta matriz de rotación y úsela para rotar la diferencia entre la pose actual y la pose anterior, alineándola con el marco de referencia del nodo de la pose anterior. Por último, reste la pose de odometría medida del resultado.

$[\begin{matrix} r e s_{x} \\ r e s_{y} \end{matrix}] = {[\begin{matrix} \cos θ_{i} & - \sin θ_{i} \\ \sin θ_{i} & \cos θ_{i} \end{matrix}]}^{T} \cdot ([\begin{matrix} x_{j} \\ y_{j} \end{matrix}] - [\begin{matrix} x_{i} \\ y_{i} \end{matrix}]) - [\begin{matrix} x_{m} \\ y_{m} \end{matrix}]$
Calcule los residuales de la orientación restando la orientación anterior y la orientación medida de la orientación actual.

$r e s_{θ} = θ_{j} - θ_{i} - θ_{m}$
Calcule los valores residuales finales tomando la raíz cuadrada de la matriz de información y multiplicándola por los residuales de pose calculados.

$r e s = \sqrt{I} \cdot [\begin{matrix} r e s_{x} \\ r e s_{y} \\ r e s_{θ} \end{matrix}]$

Cómo utilizar el objeto `factorGraph`

Esta sección muestra cómo comenzar a construir un gráfico factorial y proporciona sugerencias e información para garantizar gráficos factoriales bien construidos.

Agregar nodos y factores

La construcción de gráficos factoriales se basa en objetos factoriales que, cuando se agregan al gráfico, introducen tanto factores como cualquier nodo necesario. Un objeto de factor se conecta a uno o más nodos, dependiendo del tipo de factor que representa. Cuando se agrega un factor al gráfico, si especifica un nodo que no existe, el gráfico crea automáticamente un nodo del tipo esperado en el gráfico de factores. Por ejemplo, en este caso el gráfico está creando dos nuevos nodos POSE_SE3 con los identificadores de nodo 1 y 2 porque ninguno de los nodos existe en el gráfico de factores antes de la adición del objeto de factor.

fg = factorGraph;
f1 = factorTwoPoseSE3([1 2]);
% Add factor to factor graph and store the unique factor ID assigned by the factor graph.
fID = addFactor(fg,f1);

Pero si agrega otro factor al mismo gráfico, es posible que se esté conectando a nodos existentes. En este caso, el factor se conecta al nodo existente 2 y crea un nuevo nodo con un ID de 3.

f2 = factorTwoPoseSE3([2 3]);
addFactor(fg,f2)

Después de agregar factores al gráfico de factores, debe utilizar la función nodeState para establecer una estimación inicial del estado de cada nodo para proporcionar más información al optimizador. Por ejemplo, este código muestra cómo establecer los estados iniciales utilizando el mismo gráfico de factores.

initialGuessStates = [0 0 pi/2; 1 1 pi/4; 2 2 0] % [x y theta]
nodeState([1 2 3],initialGuessStates);

Establecer estados de estimación iniciales para los nodos mejora significativamente la precisión del gráfico de factores y ayuda a evitar que el proceso de optimización converja a mínimos locales.

Tipos de nodos de coincidencia

Al agregar factores a un gráfico de factores, asegúrese de conectar los factores a los ID de nodo del tipo de nodo correcto.

La propiedad NodeID de cada objeto de factor especifica y se conecta a estos tipos de nodos:

Objeto de factor	Tipos de nodos esperados de ID de nodos especificados
`factorGPS`	`["POSE_SE3"]`
`factorIMU`	`["POSE_SE3","VEL3","IMU_BIAS","POSE_SE3","VEL3","IMU_BIAS"]`
`factorCameraSE3AndPointXYZ`	`["POSE_SE3","POINT_XYZ"]` o `["POSE_SE3","POINT_XYZ","TRANSFORM_SE3"]`
`factorPoseSE2AndPointXY`	`["POSE_SE2","POINT_XY"]`
`factorPoseSE3AndPointXYZ`	`["POSE_SE3","POINT_XYZ"]`
`factorTwoPoseSE2`	`["POSE_SE2","POSE_SE2"]`
`factorTwoPoseSE3`	`["POSE_SE3","POSE_SE3"]`
`factorTwoPoseSIM3`	`["POSE_SE3","POSE_SE3_SCALE","POSE_SE3","POSE_SE3_SCALE"]`
`factorIMUBiasPrior`	`["IMU_BIAS"]`
`factorPoseSE3Prior`	`["POSE_SE3"]`
`factorVelocity3Prior`	`["VEL_3"]`

Por ejemplo, factorPoseSE2AndPointXY([1 2]) crea un factor de referencia 2-D que se conecta a los identificadores de nodo 1 y 2. Si intenta agregar ese factor a un gráfico de factores que ya contiene nodos con los ID 1 y 2, el factor espera que los nodos 1 y 2 sean de los tipos "POSE_SE2" y "POINT_XY", respectivamente.

También puede comprobar el tipo de nodos en el gráfico de factores utilizando la función nodeType.

fg = factorGraph;
f = factorTwoPoseSE2([1 2])
addFactor(fg,f);
typeID1 = nodeType(fg,1)

typeID1 = 
    "POSE_SE2"

Organizar y consultar nodos

Los identificadores de nodos le permiten realizar muchas operaciones de gráficos factoriales, por lo que organizar estos identificadores de nodos facilita el trabajo con grupos de nodos. Puede organizar los nodos a medida que los agrega a un gráfico de factores utilizando el argumento groupID de addFactor. Para obtener más información sobre cómo especificar identificadores de grupo, consulte el ejemplo groupID y Agregar nodos a grupos.

Usando la función nodeIDs, puedes consultar los ID de nodos en el gráfico de factores de cuatro maneras:

Todos los nodos a la vez: nodeIDs(fg); obtiene todos los nodos en el gráfico de factores.
Por tipo de nodo: nodeIDs(fg,NodeType="POSE_SE2"); obtiene todos los nodos del tipo "POSE_SE2"
Por tipo de factor: nodeIDs(fg,FactorType="factorTwoPoseSE2") obtiene todos los nodos conectados a los factores factorTwoPoseSE2.
Por ID de grupo: nodeIDs(fg,GroupID=1) obtiene todos los nodos del grupo 1.

Para obtener más información sobre cómo obtener identificadores de nodos, consulte el ejemplo Obtener ID de nodo del gráfico de factores.

Optimizar el gráfico de factores

Para optimizar el gráfico de factores, utilice la función de objeto optimize. La función de objeto optimize intenta encontrar una solución que minimice el costo del problema de mínimos cuadrados no lineales formulado por el gráfico de factores. Tenga en cuenta que el costo total del gráfico de factores es la suma de los residuales de cada factor y el cálculo de los residuos varía según el tipo de factor.

Utilice una de dos estrategias para optimizar su gráfico de factores:

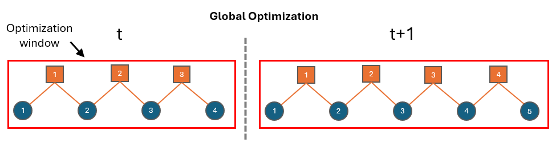
Optimización global: optimice todo el gráfico de factores cada vez que agregue nuevos nodos y factores, o después de construir completamente el gráfico. Esta estrategia puede producir resultados más precisos en comparación con el flujo de trabajo de ventana deslizante, a costa de un mayor tiempo de cálculo.
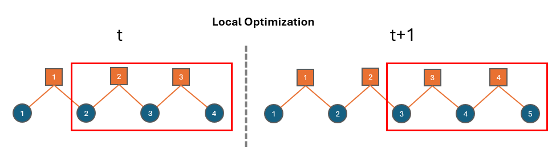
Optimización local: optimice los nodos y factores agregados más recientemente en cada paso de tiempo. Esta estrategia de optimización también se conoce como optimización de ventana deslizante. Esta estrategia es beneficiosa cuando se trabaja con gráficos de factores grandes porque minimiza la cantidad de veces que es necesario volver a optimizar partes más antiguas del gráfico de factores. Para ver un ejemplo de optimización de ventana deslizante, consulte Optimice incrementalmente el gráfico de factores mediante la ventana deslizante.

Nota

Antes de optimizar un gráfico de factores, establezca una estimación del estado inicial para todos los nodos utilizando la función nodeState.

También puede utilizar el objeto factorGraphSolverOptions para especificar y ajustar las opciones del solucionador. Para obtener más información sobre cómo ajustar las opciones del solucionador, consulte el argumento de salida solnInfo de la función de objeto optimize.

Estados de nodo de acceso y covarianza

Después de la optimización, puede acceder al estado actual de los nodos utilizando la función nodeState.

nID = 1;
states = nodeState(nID);

También puede obtener la covarianza del estado del nodo si optimizó con el cálculo de covarianza habilitado. Para habilitar el cálculo de covarianza, debe especificar opciones de solucionador personalizadas utilizando el objeto factorGraphSolverOptions, con la propiedad StateCovarianceType establecida en los tipos de nodo deseados.

nID = 1;
cov = nodeCovariance(nID);

La optimización del gráfico factorial utiliza el solucionador Ceres para la estimación de la covarianza del estado del nodo. Para obtener más información sobre la estimación de covarianza de Ceres-Solver, consulte http://ceres-solver.org/nnls_covariance.html.

Nota

La estimación de la covarianza del estado del nodo implica mayores costos de cálculo y tiempos de estimación más largos a medida que aumenta el número de nodos que se optimizan.

Tipos de nodos

Cada nodo de un gráfico factorial es uno de estos tipos y tiene un formato de estado correspondiente.

POSE_SE2 — Pose en el espacio de estados SE(2) en la forma [x y theta]. x y y son las posiciones x y y, respectivamente, y theta es la orientación.
POSE_SE3 — Pose en el espacio de estados SE(3) en la forma [x y z qw qx qy qz]. x, y y z son las posiciones x, y y z, respectivamente, y qw, qx, qy y qz representan la orientación como un cuaternión.
POSE_SE3_SCALE — Escala de pose en el espacio de estados SE(3) en forma de una variable s.
"TRANSFORM_SE3"— Transformación del sensor en el espacio de estados SE(3) en la forma [dx dy dz dqw dqx dqy dqz]. dx, dy y dz son el cambio de posición en x, y y z respectivamente. dqw, dqx, dqy y dqz son el cambio en la rotación del cuaternión en w, x, y y z, respectivamente.
VEL3 — Velocidad 3-D en la forma [vx vy vz]. vx, vy y vz son las velocidades x, y y z, respectivamente.
POINT_XY — Punto 2-D en la forma [x y]. x y y son las posiciones x y y, respectivamente.
POINT_XYZ — Punto 3D con la forma [x y z]. x, y y z son las posiciones x, y y z, respectivamente.
IMU_BIAS — Sesgo del giroscopio y del acelerómetro de la IMU en la forma [bias_gyro_x bias_gyro_y bias_gyro_z bias_accel_x bias_accel_y bias_accel_z], donde:
- bias_gyro_x, bias_gyro_y y bias_gyro_z son los sesgos del giroscopio IMU x, y y z, respectivamente.
- bias_accel_x, bias_accel_y y bias_accel_z son los sesgos del acelerómetro x, y y z, respectivamente.

Lista de factores admitidos

El objeto factorGraph admite los factores enumerados en estas secciones por objetivo.

Relacionar poses entre sí

factorTwoPoseSE2 — Conecta pares de nodos de pose SE(2) ("POSE_SE2") usando mediciones de pose relativas. Puede calcular la postura relativa utilizando el registro de escaneo LiDAR 2-D usando funciones como matchScans.
factorTwoPoseSE3 — Conecta pares de nodos de pose SE(3) ("POSE_SE3") usando mediciones de pose relativas. Puede calcular la postura relativa utilizando el registro de escaneo LiDAR 3D usando funciones como pcregistericp (Computer Vision Toolbox) y estrelpose (Computer Vision Toolbox).
factorTwoPoseSIM3 — Conecta pares de nodos de pose SIM(3) usando mediciones de pose relativas. Un nodo de pose SIM(3) se representa utilizando una combinación de un nodo de pose SE(3) ("POSE_SE3") y un nodo de escala de pose SE(3) ("POSE_SE3_SCALE"). Puede utilizar la función estgeotform3d (Computer Vision Toolbox) para calcular la medida de la pose relativa para este factor.

Relacionar poses con posiciones de punto de referencia

factorCameraSE3AndPointXYZ — Conecte el nodo de pose SE(3) de una cámara estenopeica ("POSE_SE3") a nodos de referencia 3D ("Point_XYZ"), o el nodo de pose SE(3) de una cámara estenopeica ("POSE_SE3"), nodos de referencia 3D ("Point_XYZ") y un nodo de transformación de sensor SE(3) ("TRANSFORM_SE3") utilizando las mediciones de puntos de imagen 2D de la cámara.
factorPoseSE2AndPointXY — Conecta un nodo de pose SE(2) ("POSE_SE2") a nodos de referencia 2-D ("POINT_XY") utilizando mediciones de posición 2-D en el marco de referencia del nodo de pose.
factorPoseSE3AndPointXYZ — Conecta un nodo de pose SE(3) ("POSE_SE3") a nodos de referencia 3D ("POINT_XYZ") utilizando mediciones de posición 3D en el marco de referencia del nodo de pose.

Relacionar poses con mediciones de sensores

factorGPS — Conecta un nodo de pose SE(3) ("POSE_SE3") a una medición GPS.
factorIMU — Conecte dos nodos de pose SE(3) ("POSE_SE3"), dos nodos de velocidad 3D ("VEL3") y dos nodos de sesgo IMU ("IMU_BIAS") usando mediciones IMU. Estas mediciones consisten en datos del acelerómetro y del giroscopio que capturan cambios en la postura y la velocidad.

Relacionar poses o velocidades con medidas conocidas anteriormente

Si una pose, un sesgo de IMU o una velocidad es una cantidad conocida, agregue uno de estos factores anteriores para fijar suavemente los estados del nodo, permitiendo ligeras variaciones solo si hacerlo reduce significativamente el costo general:

factorIMUBiasPrior — Conecta los nodos de pose SE(3) ("POSE_SE3"), los nodos de velocidad 3-D ("VEL3") y los nodos de sesgo de IMU ("IMU_BIAS") a mediciones de IMU conocidas previamente.
factorPoseSE3Prior — Conecta los nodos de pose SE(3) ("POSE_SE3") a las mediciones de pose SE(3) conocidas previamente.
factorVelocity3Prior — Conecta un nodo de velocidad 3-D ("VEL_3") a mediciones de velocidad SE(3) conocidas previamente.

Para los casos en los que ciertos estados de nodos no deben variar en absoluto durante la optimización, arregle los nodos utilizando la función de objeto fixNode en lugar de agregar un factor anterior.

Consulte también

factorGraph | factorGraphSolverOptions