Distribución t de Student
Visión general
La distribución t de Student es una familia de curvas de un parámetro. La distribución se suele utilizar para probar una hipótesis relacionada con la media de la población cuando la desviación estándar de la población es desconocida.
Statistics and Machine Learning Toolbox™ ofrece varias formas de trabajar con la distribución t de Student.
Utilice funciones específicas de la distribución (
tcdf,tinv,tpdf,trndytstat) con parámetros de distribución especificados. Las funciones específicas de la distribución pueden aceptar parámetros de varias distribuciones t de Student.Utilice funciones de distribución genéricas (
cdf,icdf,pdf,random) con un nombre de distribución específico ('T') y parámetros.
Parámetros
La distribución t de Student utiliza el siguiente parámetro.
| Parámetro | Descripción | Soporte |
|---|---|---|
| nu (ν) | Grados de libertad | ν = 1, 2, 3,... |
Función de densidad de probabilidad
La pdf de la distribución t de Student es
donde ν son los grados de libertad, y Γ( · ) es la función gamma. El resultado y es la probabilidad de observar un valor en particular de x a partir de la distribución t de Student con ν grados de libertad.
Para ver un ejemplo, consulte Calcular y representar la pdf de una distribución t de Student.
Función de distribución acumulativa
La cdf de la distribución t de Student es
donde ν son los grados de libertad, y Γ( · ) es la función gamma. El resultado p es la probabilidad de que una sola observación a partir de la distribución t con ν grados de libertad quede en el intervalo [–∞, x].
Para ver un ejemplo, consulte Calcular y representar la cdf de una distribución t de Student.
Función de distribución acumulativa inversa
La función inversa t se define en términos de la cdf de la t de Student como
donde
ν son los grados de libertad, y Γ( · ) es la función gamma. El resultado x es la solución de la ecuación integral, en la que usted proporciona la probabilidad p.
Para ver un ejemplo, consulte Calcular la icdf de la t de Student.
Estadísticas descriptivas
La media de la distribución t de Student es μ = 0 para los grados de libertad ν mayores que 1. Si ν es igual a 1, la media es indefinida.
La varianza de la distribución t de Student es para los grados de libertad ν mayores que 2. Si ν es menor que o igual a 2, la varianza es indefinida.
Ejemplos
Calcular y representar la pdf de una distribución t de Student
Calcule la pdf de una distribución t de Student con grados de libertad iguales a 5, 10 y 50.
x = [-5:.1:5]; y1 = tpdf(x,5); y2 = tpdf(x,10); y3 = tpdf(x,50);
Represente las pdf de las tres opciones de nu en el mismo eje.
figure; plot(x,y1,'Color','black','LineStyle','-') hold on plot(x,y2,'Color','red','LineStyle','-.') plot(x,y3,'Color','blue','LineStyle','--') xlabel('Observation') ylabel('Probability Density') legend({'nu = 5','nu = 10','nu = 50'}) hold off

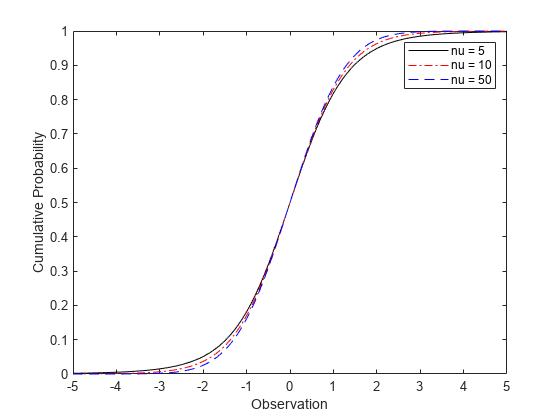
Calcular y representar la cdf de una distribución t de Student
Calcule la cdf de una distribución t de Student con grados de libertad iguales a 5, 10 y 50.
x = [-5:.1:5]; y1 = tcdf(x,5); y2 = tcdf(x,10); y3 = tcdf(x,50);
Represente las cdf de las tres opciones de nu en el mismo eje.
figure; plot(x,y1,'Color','black','LineStyle','-') hold on plot(x,y2,'Color','red','LineStyle','-.') plot(x,y3,'Color','blue','LineStyle','--') xlabel('Observation') ylabel('Cumulative Probability') legend({'nu = 5','nu = 10','nu = 50'}) hold off
Calcular la icdf de la t de Student
Encuentre el percentil 95 de la distribución t de Student con 50 grados de libertad.
p = .95; nu = 50; x = tinv(p,nu)
x = 1.6759
Comparar las pdf de la distribución normal y t de Student
La distribución t de Student es una familia de curvas que depende de un solo parámetro v (los grados de libertad). A medida que los grados de libertad de v se acercan a infinito, la distribución t se acerca a la distribución normal estándar.
Calcule las pdf de la distribución t de Student con el parámetro nu = 5 y la distribución t de Student con el parámetro nu = 15.
x = [-5:0.1:5]; y1 = tpdf(x,5); y2 = tpdf(x,15);
Calcule la pdf de una distribución normal estándar.
z = normpdf(x,0,1);
Represente las pdf de la distribución t de Student y la pdf normal estándar en la misma figura.
plot(x,y1,'-.',x,y2,'--',x,z,'-') legend('Student''s t Distribution with \nu=5', ... 'Student''s t Distribution with \nu=15', ... 'Standard Normal Distribution','Location','best') xlabel('Observation') ylabel('Probability Density') title('Student''s t and Standard Normal pdfs')

La pdf normal estándar tiene colas más breves que las pdf de la distribución t de Student.
Distribuciones relacionadas
Beta Distribution — La distribución beta es una distribución continua de dos parámetros que tiene los parámetros a (primer parámetro de forma) y b (segundo parámetro de forma). Si Y tiene una distribución t de Student con ν grados de libertad, tiene una distribución beta con los parámetros de forma a = ν/2 y b = ν/2. Esta relación se utiliza para calcular valores de la cdf t y funciones inversas, y para generar números aleatorios distribuidos en t.
Distribución de Cauchy — La distribución de Cauchy es una distribución continua de dos parámetros con los parámetros γ (escala) y δ (localización). Es un caso especial de Stable Distribution con los parámetros de forma α = 1 y β = 0. La distribución estándar de Cauchy (escala unitaria y localización cero) es la distribución t de Student con grados de libertad ν igual a 1. La distribución estándar de Cauchy tiene una media y una varianza indefinidas.
Para ver un ejemplo, consulte Generar números aleatorios de Cauchy utilizando la t de Student.
Distribución chi-cuadrado — La distribución chi-cuadrado es una distribución continua de un parámetro que tiene el parámetro ν (grados de libertad). Si Z tiene una distribución normal estándar, χ2 tiene una distribución chi-cuadrado y Z y χ2 son independientes con grados de libertad de ν, tiene una distribución t de Student con grados de libertad de ν.
Noncentral t Distribution — La distribución t no central es una distribución continua de dos parámetros que generaliza la distribución t de Student y tiene los parámetros ν (grados de libertad) y δ (no centralidad). Si se ajusta δ = 0 se obtiene la distribución t de Student.
Distribución normal — La distribución normal es una distribución continua de dos parámetros con los parámetros μ (media) y σ (desviación estándar).
A medida que los grados de libertad de ν se acercan a infinito, la distribución t de Student se acerca a la distribución normal estándar (media de cero y desviación estándar de unidad).
Para ver un ejemplo, consulte Comparar las pdf de la distribución normal y t de Student
Si x es una muestra aleatoria de tamaño n de una distribución normal con una media de μ, la estadística , en la que es la media de la muestra y s es la desviación estándar de la muestra, tiene una distribución t de Student con n —1 grados de libertad.
Para ver un ejemplo, consulte Calcular la cdf de la distribución t de Student.
t Location-Scale Distribution — La distribución t de localización y escala es una distribución continua de tres parámetros con los parámetros μ (media), σ (escala) y ν (forma). Si x tiene una distribución t de localización y escala con los parámetros µ, σ y ν, tiene una distribución t de Student con ν grados de libertad.
Referencias
[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.
[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8
[3] Evans, Merran, Nicholas Hastings, and Brian Peacock. Statistical Distributions. 2nd ed. New York: J. Wiley, 1993.
[4] Kreyszig, Erwin. Introductory Mathematical Statistics: Principles and Methods. New York: Wiley, 1970.
Consulte también
tcdf | tpdf | tinv | tstat | trnd | ttest | ttest2